 HELP ME TUI ĐANG CẦN GẤP !!!
HELP ME TUI ĐANG CẦN GẤP !!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c) \(\left|x\right|=3,5\Rightarrow\left[{}\begin{matrix}x=3,5\\x=-3,5\end{matrix}\right.\)
d) \(\left|x\right|=-2,7\Rightarrow x\in\varnothing\)
l) \(\left|x+\dfrac{3}{4}\right|-5=-2\Rightarrow\left|x+\dfrac{3}{4}\right|=3\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=3\\x+\dfrac{3}{4}=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3-\dfrac{3}{4}\\x=-3-\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{9}{4}\\x=\dfrac{15}{4}\end{matrix}\right.\)
Đính chính câu l \(x=-\dfrac{15}{4}\) không phải \(x=\dfrac{15}{4}\)

\(\left|x-1\right|+\left|x-2\right|+\left|x-3\right|+\left|x-4\right|+\left|x-5\right|=6\left(1\right)\)
Tìm các nghiệm sau :
\(x-1=0\Rightarrow x=1\)
\(x-2=0\Rightarrow x=2\)
\(x-3=0\Rightarrow x=3\)
\(x-4=0\Rightarrow x=4\)
\(x-5=0\Rightarrow x=5\)
Bảng xét dấu
\(|\)
| \(x\) | \(1\) \(2\) \(3\) \(4\) \(5\) |
| \(x-1\) | - \(0\) + \(|\) + \(|\) + \(|\) + \(|\) + |
| \(x-2\) | - \(|\) - \(0\) + \(|\) + \(|\) + \(|\) + |
| \(x-3\) | - \(|\) - \(|\) - \(0\) + \(|\) + \(|\) + |
| \(x-4\) | - \(|\) - \(|\) - \(|\) - \(0\) + \(|\) + |
| \(x-5\) | - \(|\) - \(|\) - \(|\) \(|\) \(|\) - \(0\) + |
- Nếu \(x< 1\)
\(\left(1\right)\Rightarrow-x+1-x+2-x+3-x+4-x+5=6\)
\(\Rightarrow-5x+15=6\Rightarrow5x=9\Rightarrow x=\dfrac{9}{5}\left(loại\right)\)
- Nếu \(1\le x\le2\)
\(\left(1\right)\Rightarrow x-1-x+2-x+3-x+4-x+5=6\)
\(\Rightarrow-3x+13=6\Rightarrow3x=7\Rightarrow x=\dfrac{7}{3}\left(loại\right)\)
- Nếu \(2\le x\le3\)
\(\left(1\right)\Rightarrow x-1+x-2-x+3-x+4-x+5=6\)
\(\Rightarrow-x+10=6\Rightarrow x=4\left(loại\right)\)
- Nếu \(3\le x\le4\)
\(\left(1\right)\Rightarrow x-1+x-2+x-3-x+4-x+5=6\)
\(\Rightarrow x+7=6\Rightarrow x=-1\left(loại\right)\)
- Nếu \(4\le x\le5\)
\(\left(1\right)\Rightarrow x-1+x-2+x-3+x-4-x+5=6\)
\(\Rightarrow3x-5=6\Rightarrow3x=11\Rightarrow x=\dfrac{11}{3}\left(loại\right)\)
- Nếu \(x>5\)
\(\left(1\right)\Rightarrow x-1+x-2+x-3+x-4+x-5=6\)
\(\Rightarrow5x-15=6\Rightarrow5x=21\Rightarrow x=\dfrac{21}{5}\left(nhận\right)\)
Vậy \(x=\dfrac{21}{5}\) thỏa phương trình theo đề bài
mong bạn tik cho mình
Để giải phương trình |x - 1| + |x - 2| + |x - 3| + |x - 4| + |x - 5| = 6, chúng ta cần xem xét từng khoảng giá trị của x để tìm ra các giải pháp.
Chúng ta biết rằng giá trị tuyệt đối của một số luôn không âm (không nhỏ hơn 0). Vì vậy, trong trường hợp này, chúng ta có thể xét các khoảng giá trị của x dựa trên các điểm 1, 2, 3, 4 và 5.
Khi x ≤ 1:
|x - 1| = 1 - x
|x - 2| = 2 - x
|x - 3| = 3 - x
|x - 4| = 4 - x
|x - 5| = 5 - x
Thế vào phương trình: (1 - x) + (2 - x) + (3 - x) + (4 - x) + (5 - x) = 6 -5x + 15 = 6 -5x = -9 x = 9/5
Tuy nhiên, x ≤ 1 mà x = 9/5 không thỏa mãn điều kiện, nên không có nghiệm trong khoảng này.
Khi 1 < x ≤ 2:
|x - 1| = x - 1
|x - 2| = 2 - x
|x - 3| = 3 - x
|x - 4| = 4 - x
|x - 5| = 5 - x
Thế vào phương trình: (x - 1) + (2 - x) + (3 - x) + (4 - x) + (5 - x) = 6 3 - x = 6 -x = 3 x = -3
Tuy nhiên, 1 < x ≤ 2 mà x = -3 không thỏa mãn điều kiện, nên cũng không có nghiệm trong khoảng này.
Tiếp tục thử các khoảng giá trị tiếp theo, ta sẽ nhận thấy rằng không có giá trị nào của x trong các khoảng từ 2 đến 5 thỏa mãn phương trình.
Khi x > 5:
|x - 1| = x - 1
|x - 2| = x - 2
|x - 3| = x - 3
|x - 4| = x - 4
|x - 5| = x - 5
Thế vào phương trình: (x - 1) + (x - 2) + (x - 3) + (x - 4) + (x - 5) = 6 5x - 15 = 6 5x = 21 x = 21/5
Với khoảng giá trị x > 5, x = 21/5 thỏa mãn phương trình.
Vậy, phương trình có một nghiệm duy nhất là x = 21/5 khi x thuộc khoảng (5, +∞).

Lời giải:
Áp dụng BĐT $|a|+|b|\geq |a+b|$ ta có:
$|x-1|+|x-5|=|x-1|+|5-x|\geq |x-1+5-x|=4$
$|x-2|+|x-4|=|x-2|+|4-x|\geq |x-2+4-x|=2$
$|x-3|\geq 0$
$\Rightarrow |x-1|+|x-2|+|x-3|+|x-4|+|x-5|\geq 4+2+0=6$
Dấu "=" xảy ra khi: \(\left\{\begin{matrix} (x-1)(5-x)\geq 0\\ (x-2)(4-x)\geq 0\\ x-3=0\end{matrix}\right.\Leftrightarrow x=3\)

Ta có: \(\dfrac{x^2}{-2}=-8\)
\(\Rightarrow x^2=-8\cdot-2=16\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
Khi x=4:
\(B=-\left(4+1\right)^2+\dfrac{1}{2}\cdot\left(-3-3\right)^3=-25\)
Khi x=-4:
\(B=-\left(-4+1\right)^2+\dfrac{1}{2}\cdot\left(-3-3\right)^3=-117\)

Ta đặt
\(A=\dfrac{1}{50}-\dfrac{1}{50\times49}-....-\dfrac{1}{2\times1}\)
\(A=\dfrac{1}{50}-\left(\dfrac{1}{1\times2}+\dfrac{1}{2\times3}+...+\dfrac{1}{49\times50}\right)\)
\(A=\dfrac{1}{50}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)\)
\(A=\dfrac{1}{50}-\left(1-\dfrac{1}{50}\right)\)
\(A=\dfrac{1}{50}-\dfrac{49}{50}\)
\(A=\dfrac{-48}{50}=\dfrac{-24}{25}\)
\(=\dfrac{1}{50}-\left(\dfrac{2-1}{1.2}+\dfrac{3-2}{2.3}+\dfrac{4-3}{3.4}+...+\dfrac{50-49}{49.50}\right)=\)
\(=\dfrac{1}{50}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)=\)
\(=\dfrac{1}{50}-\left(1-\dfrac{1}{50}\right)=\dfrac{2}{50}-1=\dfrac{1}{25}-1=-\dfrac{24}{25}\)

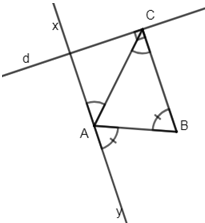
a) Ta có: ˆCAx=ˆACB(gt)���^=���^(��) mà hai góc đó là hai góc so le trong nên
suy ra Ax//BC��//�� (1)
ˆBAy=ˆABC(gt)���^=���^(��) mà hai góc đó là hai góc so le trong nên suy ra Ay//BC��//�� (2)
Từ (1) và (2) suy ra Ax và Ay cùng // BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
⇒⇒ Ax và Ay là hai tia đối nhau.
b) Vì Ax và Ay là hai tia đối nhau (cmt) mà Ax//BC��//�� và Ay//BC��//��
nên suy ra xy//BC��//��
Mà BC⊥d��⊥� nên suy ra d⊥xy

Ta có: l x+1l lớn hơn hoặc bằng 0, với mọi x
l 2y -3l lớn hơn hoặc bằng 0, với mọi y
=> l x+1l + l 2y-3l lớn hơn hoặc bằng 0, với mọi x,y
=> l x+1l + l 2y-3l + 5 lớn hơn hoặc bằng 5
=> 1/ lx+1l + l2y-3l + 5 bé hơn hoặc bằng 1/5
=> 20/ lx+1l + l2y-3l+5 bé hơn hoặc bằng 20/5 = 4
Vậy max Q = 4
Dẫu "=" xảy ra <=> x = -1 ; y = 3/2
Chúc bạn học tốt!
Ta có: l x+1l lớn hơn hoặc bằng 0, với mọi x
l 2y -3l lớn hơn hoặc bằng 0, với mọi y
=> l x+1l + l 2y-3l lớn hơn hoặc bằng 0, với mọi x,y
=> l x+1l + l 2y-3l + 5 lớn hơn hoặc bằng 5
=> 1/ lx+1l + l2y-3l + 5 bé hơn hoặc bằng 1/5
=> 20/ lx+1l + l2y-3l+5 bé hơn hoặc bằng 20/5 = 4
Vậy max Q = 4
Dẫu "=" xảy ra <=> x = -1 ; y = 3/2