96

96

Tổng của ba số là: 81 + 59 + 16 = 156

Ta có sơ đồ:

Theo sơ đồ ta có: Số a là: 156:( 4 -1) = 52

Đáp số: 52

Thử lại kết quả ta có:

Tổng của 4 số là: 81 + 59 + 16 + 52 = 208

Trung bình cộng của cả bốn số là: 208 : 4  =52 

Trung bình cộng của 4 số bằng số a (ok nha em )

4 - Tìm một số có ba chữ số mà khi viết thêm vào bên trái số đó một chữ số 9 thì được số mới lớn hơn số phải tìm 13 lần.

5 - Trong kho có 1298kg đỗ  gồm đỗ xanh, đỗ đen và đỗ đỏ.  số đỗ xanh thì bằng  số đỗ đen. Số đỗ đỏ thì bằng một nửa số đỗ xanh. Mỗi loại đỗ có bao nhiêu ki-lô-gam?

- Tìm trung bình cộng các số tự nhiên nhỏ hơn 99.

Ta biến đổi \(A=\dfrac{2-1}{1.2}+\dfrac{4-3}{3.4}+...+\dfrac{2016-2015}{2016.2015}+\dfrac{2018-2017}{2017.2018}\) 

\(A=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2015}-\dfrac{1}{2016}+\dfrac{1}{2017}-\dfrac{1}{2018}\)

\(A=\left(1+\dfrac{1}{3}+...+\dfrac{1}{2017}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2018}\right)\)

\(A=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2017}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2018}\right)\)

\(A=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2017}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{1009}\right)\)

\(A=\dfrac{1}{1010}+\dfrac{1}{1011}+...+\dfrac{1}{2017}+\dfrac{1}{2018}\)

Lại có \(B=\dfrac{1}{1010.2018}+\dfrac{1}{1011.2017}+...+\dfrac{1}{2018.1010}\)

\(B=\dfrac{1}{3028}.\left(\dfrac{3028}{1010.2018}+\dfrac{3028}{1011.2017}+...+\dfrac{3028}{2018.1010}\right)\)

\(B=\dfrac{1}{3028}\left(\dfrac{1}{1010}+\dfrac{1}{2018}+\dfrac{1}{1011}+\dfrac{1}{2017}+...+\dfrac{1}{2018}+\dfrac{1}{1010}\right)\)

\(B=\dfrac{1}{3028}.2\left(\dfrac{1}{1010}+\dfrac{1}{1011}+...+\dfrac{1}{2018}\right)\)

\(B=\dfrac{1}{3028}.2A\) \(\Rightarrow\dfrac{A}{B}=1514\inℤ\). Ta có đpcm

Dùng giả thiết tạm kết hợp với giải ngược của tiểu học em nhé.

Giả sử lần thứ hai bà chỉ bán \(\dfrac{2}{3}\) số cam còn lại thì sau hai lần bán bà còn số cam là:

8 + 1  = 9 (quả)

9 quả ứng với phân số là:

1 - \(\dfrac{2}{3}\) = \(\dfrac{1}{3}\) (số cam còn lại sau lần bán thứ nhất)

Số cam còn lại sau lần bán thứ nhất là:

9 : \(\dfrac{1}{3}\) = 27 (quả)

Giả sử lần thứ nhất bà chỉ bán \(\dfrac{3}{4}\) số cam thì sau lần bán thứ nhất bà còn số cam là:

    27 + 3  = 30(quả)

30 quả ứng với phân số là: 1 - \(\dfrac{3}{4}\) = \(\dfrac{1}{4}\) (số cam)

Ban đầu bà có số cam là: 30 : \(\dfrac{1}{4}\) = 120 (quả)

Đáp số: 120 quả

Thử lại kết quả bài toán ta có:

Lần thứ nhất bà bán số cam là: 120 \(\times\) \(\dfrac{3}{4}\) + 3 = 93 (quả)

Số cam còn lại sau lần bán thứ nhất là:120 - 93 = 27 (quả)

Số cam bà bán lần thứ hai là: 27 \(\times\) \(\dfrac{2}{3}\) + 1 = 19 (quả)

Số cam còn lại sau hai lần bán là: 27 - 19 = 8 (quả) ok nha em

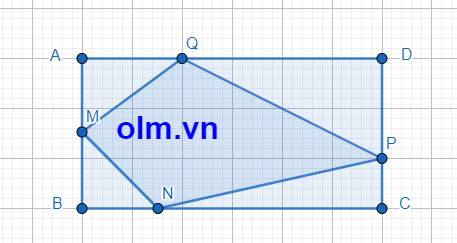
A B C D M N P Q

Hình tớ vẽ hơi xấu, bạn thông cảm nhé.

Ta có \(S\Delta AMQ=\dfrac{1}{2}.AM.AQ=\dfrac{1}{2}.\dfrac{1}{2}AB.\dfrac{1}{3}AD\)

\(=\dfrac{1}{12}.288=24\left(cm^2\right)\)

   \(S\Delta MBN=\dfrac{1}{2}MB.BN=\dfrac{1}{2}.\dfrac{1}{2}AB.\dfrac{1}{4}BC\)

\(=\dfrac{1}{16}.288=18\left(cm^2\right)\)

   \(S\Delta QDP=\dfrac{1}{2}QD.DP=\dfrac{1}{2}.\dfrac{2}{3}AD.\dfrac{2}{3}DC\)

\(=\dfrac{2}{9}.288=64\left(cm^2\right)\)

  \(S\Delta NPC=\dfrac{1}{2}.NC.CP=\dfrac{1}{2}.\dfrac{3}{4}BC.\dfrac{1}{3}.DC\)

\(=\dfrac{1}{8}.288=36\left(cm^2\right)\)

\(S_{MNPQ}=288-36-64-18-24=146\left(cm^2\right)\)

DQ + QA = DA ⇒ QA = DA - DQ = DA - \(\dfrac{2}{3}\)DA = \(\dfrac{1}{3}\)DA

S_AMQ = \(\dfrac{1}{3}\)S_{ADM( Vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy AD và AQ = \(\dfrac{1}{3}\)AD)} 

S_ADM = \(\dfrac{1}{2}\)S_{ABD(vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AB và AM = \(\dfrac{1}{2}\)AB})

S_ABD = \(\dfrac{1}{2}\)S_ABCD(vì ABCD là hình chữ nhật)

⇒S_AMQ = \(\dfrac{1}{3}\times\dfrac{1}{2}\times\dfrac{1}{2}\)\(\times\)S_ABCD = 288 \(\times\) \(\dfrac{1}{12}\)= 24 (cm²)

S_DPQ = \(\dfrac{2}{3}\)S_{ADP(vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy AD và DQ = \(\dfrac{2}{3}\)DA)}

DP = DC - CP = DC - \(\dfrac{1}{3}\)DC = \(\dfrac{2}{3}\)DC

S_ADP = \(\dfrac{2}{3}\)S_ACD(Vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DC và DP = \(\dfrac{2}{3}\) DC)

S_ACD = \(\dfrac{1}{2}\)S_ABCD

⇒S_DPQ = \(\dfrac{2}{3}\times\dfrac{2}{3}\times\)\(\dfrac{1}{2}\)\(\times\)S_ABCD = 288 \(\times\) \(\dfrac{2}{9}\)= 64 (cm²)

CN = BC - BN = BC - \(\dfrac{1}{4}\)BC = \(\dfrac{3}{4}\)BC

S_CNP = \(\dfrac{3}{4}\)S_{CBP(vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{3}{4}\)BC)}

S_CBP =  \(\dfrac{1}{3}\)S_BCD(vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đấy CD và CP = \(\dfrac{1}{3}\) CD)

S_BCD = \(\dfrac{1}{2}\)S_ABCD (vì ABCD là hình chữ nhật)

⇒S_CNP = \(\dfrac{3}{4}\times\dfrac{1}{3}\times\dfrac{1}{2}\) S_ABCD =  288 \(\times\) \(\dfrac{1}{8}\) = 36 (cm2)

S_BMN = \(\dfrac{1}{4}\)S_BCM (Vì hai  tam giác có chung đường cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{1}{4}\)BC)

S_BCM = \(\dfrac{1}{2}\)S_ABC(Vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM =\(\dfrac{1}{2}\)AB)

S_ABC =  \(\dfrac{1}{2}\)S_{ABCD(vì ABCD là hình chữ nhật)}

⇒ S_BMN = \(\dfrac{1}{4}\times\dfrac{1}{2}\times\dfrac{1}{2}\)\(\times\)S_ABCD = 288 \(\times\)\(\dfrac{1}{16}\)  = 18 (cm²)

 S_MNPQ =  S_ABCD  - (S_AMQ +S_DPQ+S_CNP+S_BMN)

Diện tích của MNPQ là:

 288 - (64 + 24 + 36 + 18) =  146 (cm2)

Đáp số: 146 cm2

`x/(2*2)+x/(3*4)+x/(6*4)+x/(8*5)+x/(10*6)=5`

`x/4 +x/12 +x/24 +x/45 + x/60 =5`

`x(1/4 +1/12 +1/24 +1/40 +1/60)=5`

`x( (30+10+5+3+2)/120 ) =5`

`x *50/120 =5`

`x = 5 *120/50 =12`

\(\dfrac{x}{4}+\dfrac{x}{12}+\dfrac{x}{24}+\dfrac{x}{40}+\dfrac{x}{60}=5\)

\(\Leftrightarrow x\left(\dfrac{1}{4}+\dfrac{1}{12}+\dfrac{1}{24}+\dfrac{1}{40}+\dfrac{1}{60}\right)=5\)

\(\Leftrightarrow x.\dfrac{5}{12}=5\)

\(\Leftrightarrow x=12\)

Gọi số cần tìm là x(x>0)

Theo bài ra ta có:

\(\dfrac{17+x}{46-x}=\dfrac{4}{5}\)

\(\Leftrightarrow5\left(17+x\right)=4\left(46-x\right)\)

\(\Leftrightarrow85+5x=184-4x\)

\(\Leftrightarrow9x=99\)

\(\Leftrightarrow x=11\)

Khi ta cộng vào tử số đồng thời bớt đi ở mẫu số cùng một số thì tổng của tử số và mẫu số không thay đổi

Tổng của tử số lúc sau và mẫu số lúc sau là: 17 + 46 = 63

Tỉ số của tử số lúc sau và mẫu số lúc sau là: \(\dfrac{4}{5}\)

Ta có sơ đồ: 

Theo sơ đồ: Tử số lúc là: 63: (4+5)\(\times\)4 = 28

                    Số cần thêm vào tử số và bớt đi ở mẫu số để được phấn số có già trị bằng\(\dfrac{4}{5}\) là:

                        28 - 17 = 11

Đáp số: 11

\(\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\)

\(=2x^2+3x-10x-15-2x^2+6x+x+7\) ( Nhân phân phối )

\(=\left(2x^2-2x^2\right)+\left(3x-10x+6x+x\right)+\left(-15+7\right)\)

\(=0+0x-8\)

\(=-8\)

Vậy biểu thức có giá trị không phụ thuộc vào giá trị của biến.

HD: Tuần có 7 ngày

Tháng có 3 ngày chủ nhật là ngày chẵn thì tháng đó có 5 ngày chủ nhật và ngày chủ nhật đầu tiên của tháng phải là ngày mồng 2.

Vậy chủ nhật cuối cùng của tháng là ngày 30

\(\dfrac{3}{7}\) < \(\dfrac{◻}{12}\) < \(\dfrac{4}{7}\)

Gọi số cần điền vào \(◻\) là \(x\) 

Ta có: \(\dfrac{3}{7}\) <  \(\dfrac{x}{12}\) < \(\dfrac{4}{7}\)

          \(\dfrac{3\times12}{7\times12}\)   < \(\dfrac{x\times7}{7\times12}\) < \(\dfrac{4\times12}{7\times12}\)

          \(\dfrac{36}{84}\) <    \(\dfrac{x\times7}{84}\)  < \(\dfrac{48}{84}\)

             36 < \(x\times7\) <  48

              36: 7 < \(x\) < 48: 7

                5,1 < \(x\) < 6,8

     Vì \(x\) là số tự nhiên nên \(x\)  = 6

Vậy số cần điền vào chỗ \(◻\) là 6

Đáp số: 6 

Gọi số cần điền vào ô trống là x ( x>0 )

Theo bài ra ta có:

\(\dfrac{3}{7}< \dfrac{x}{12}< \dfrac{4}{7}\)

\(\Leftrightarrow\dfrac{36}{84}< \dfrac{7x}{84}< \dfrac{48}{84}\)

\(\Rightarrow36< 7x< 48\)

\(\Leftrightarrow5,14< x< 6,86\)

mà x là số tự nhiên

\(\Rightarrow x=6\)