n+5 chia hết cho n-2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lượng nước mà vòi đó cần chảy thêm để đầy bể là:
1 - 3/4 = 1/4 (thể tích bể)
Để chảy đầy bể từ 9h18p vòi đó mất:
(1/4 : 1/3) x 1= 3/4 (giờ) = 45 phút
Vòi đó chảy đầy bể vào lúc:
9 giờ 18 phút + 45 phút = 9 giờ 63 phút = 10 giờ 3 phút
Đ.số: 10 giờ 3 phút

Để tìm phân số có mẫu là 10, lớn hơn -3/4 và bé hơn -3/5, ta cần tìm một phân số âm có tử số nhỏ hơn mẫu số và lớn hơn -3/4.
Ta có thể chọn phân số -2/10. Vì -2/10 = -1/5 và -1/5 lớn hơn -3/4 và bé hơn -3/5.
Vậy, phân số cần tìm là -2/10.

Số phần tử của không gian mẫu \(\left|\Omega\right|=C^3_{19}\)
Gọi A là biến cố: "An chọn ra 3 quả cho tổng chia hết cho 4."
Trong các số từ 1 đến 19 sẽ có 4 số chia hết cho 4; 5 số chia 4 dư 1; 5 số chia 4 dư 2 và 5 số chia 4 dư 3. Để tổng các số trên 3 quả chia hết cho 4 thì số dư của bộ số đó khi chia cho 4 (ta gọi là \(\left(a,b,c\right)\)) phải bằng 1 trong các bộ số sau:
\(\left(0,0,0\right)\), \(\left(0,1,3\right),\left(0,2,2\right),\left(1,1,2\right),\left(3,3,2\right)\).
Với TH \(\left(a,b,c\right)\rightarrow\left(0,0,0\right)\) thì có tất cả \(C^3_4=4\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(0,1,3\right)\) thì có tất cả \(4.5^2=100\) cách chọn
Với TH \(\left(a,b,c\right)\rightarrow\left(0,2,2\right)\) thì có tất cả \(4.C^2_5=40\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(1,1,2\right)\) thì có tất cả \(C^2_5.5=50\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(3,3,2\right)\) thì có tất cả \(C^2_5.5=50\) cách chọn.
Vậy \(\left|A\right|=4+100+40+50+50=244\).
\(\Rightarrow P\left(A\right)=\dfrac{\left|A\right|}{\left|\Omega\right|}=\dfrac{244}{C^3_{19}}=\dfrac{244}{969}\).
Vậy xác suất để An chọn ra 3 quả có tổng chia hết cho 4 là \(\dfrac{244}{969}\)

a, để tính tổng A = 1 + 2 + 3 + 4 + … + 99 + 100, ta áp dụng công thức tổng của dãy số từ 1 đến n: S = (n * (n + 1)) / 2.
Với n = 100, ta có: A = (100 * (100 + 1)) / 2 = 5050.
b, để tính tổng B = 4 + 7 + 10 + 13 + … + 301, ta nhận thấy các số trong dãy này tạo thành một cấp số cộng với công sai d = 3.
Ta có công thức tổng của cấp số cộng: S = (n/2) * (a + l), trong đó n là số phần tử, a là số đầu tiên, l là số cuối cùng.
Số đầu tiên a = 4, số cuối cùng l = 301, và công sai d = 3.
Số phần tử n = ((l - a) / d) + 1 = ((301 - 4) / 3) + 1 = 100.
Vậy tổng B = (100/2) * (4 + 301) = 50 * 305 = 15250.
B2, để tính tổng của tất cả các số tự nhiên x, biết x là số có 2 chữ số và 12 < x < 91, ta cần tính tổng các số từ 13 đến 90.
Áp dụng công thức tổng của dãy số từ a đến b: S = ((b - a + 1) * (a + b)) / 2.
Với a = 13 và b = 90, ta có: S = ((90 - 13 + 1) * (13 + 90)) / 2 = (78 * 103) / 2 = 4014.
B3, để tính tổng của tất cả các số tự nhiên a, biết a có 3 chữ số và 119 < a < 501, ta cần tính tổng các số từ 120 đến 500.
Áp dụng công thức tổng của dãy số từ a đến b: S = ((b - a + 1) * (a + b)) / 2.
Với a = 120 và b = 500, ta có: S = ((500 - 120 + 1) * (120 + 500)) / 2 = (381 * 620) / 2 = 118260.

Số tiền còn lại sau khi ủng hộ quỹ: 1,570,000 - 500,000 = 1,070,000 đồng
Số tiền mẹ bù thêm: 712,000 đồng
Số tiền Tùng Lâm đã mua đôi giày: 1,070,000 + 712,000 = 1,782,000 đồng
Vậy đôi giày của Tùng Lâm đã mua với số tiền là 1,782,000 đồng.

4 - \(\dfrac{2}{5}\) = \(\dfrac{20}{5}\) - \(\dfrac{2}{5}\) = \(\dfrac{18}{5}\)
\(\dfrac{15}{4}\) - 2 = \(\dfrac{15}{4}\) - \(\dfrac{8}{4}\) = \(\dfrac{7}{4}\)
\(\dfrac{23}{6}\) - 3 = \(\dfrac{23}{6}\) - \(\dfrac{18}{6}\) = \(\dfrac{5}{6}\)

\(a.2^{x+2}-2^x=96\\ 2^x\cdot4-2^x=96\\ 2^x\cdot\left(4-1\right)=96\\ 2^x\cdot3=96\\ 2^x=96:3\\ 2^x=32\\ 2^x=2^5\\ =>x=5\)
\(2^{x+1}\cdot3^y=12^x\\ 2^{x+1}\cdot3^y=3^x\cdot2^{2x}\\ \left\{{}\begin{matrix}2^{x+1}=2^{2x}\\3^y=3^x\end{matrix}\right.\\ \left\{{}\begin{matrix}x+1=2x\\y=x\end{matrix}\right.\\ \left\{{}\begin{matrix}x=1\\y=x=1\end{matrix}\right.\\ \left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
\(c.10^x:5^y=20^y\\ 10^x:5^y=5^y\cdot4^y\\ 10^x=10^{2y}\\ =>x=2y\)

Vì mỗi số đều là số có 5 chữ số nên số chữ số của cả hai số là:
5 + 5 = 10 ( chữ số)
Chữ số lớn nhất là 9 nên nếu tất cả các chữ số của hai số đều là chữ số 9 thì tổng các chữ số của hai số là:
9 \(\times\) 10 = 90
So với đề bài thì thừa ra :
90 - 89 = 1 đơn vị, vậy có một chữ số là 8
Để được tổng nhỏ nhất thì số hạng phải nhỏ nhất có thể, vậy số bé là: 89999; số lớn là 99999
Đáp số: hai số cần tìm lần lượt là: 89999; 99999
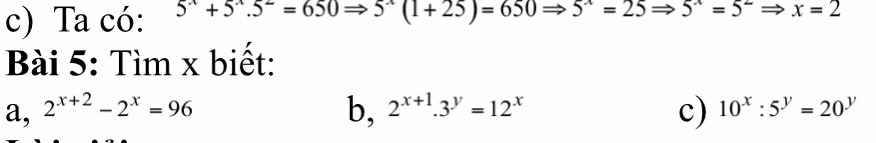
Để : \((n+5)⋮(n-2)\left(+\right)\)
\(\Leftrightarrow\dfrac{n+5}{n-2}\inℤ\Leftrightarrow\dfrac{n-2+7}{n-2}\inℤ\)
\(\Leftrightarrow1+\dfrac{7}{n-2}\inℤ\)
Vì \(1\inℤ\) nên để \(\left(+\right)\inℤ\)
\(\Leftrightarrow\dfrac{7}{n-2}\inℤ\)
\(\Leftrightarrow7⋮\left(n-2\right)\)
\(\Leftrightarrow\left(n-2\right)\inƯ\left(7\right)\)
Ta có : \(Ư\left(7\right)=\left(\pm1;\pm7\right)\)
Lập bảng ra ta thấy : Các giá trị n thoả mãn là :
\(n\in\left\{3;1;10;-5\right\}\)
\(Vậy.........\)
Theo đề (n+5)⋮(n−2)
(n+5) –(n-2)⋮(n−2)
n+5 –n-2⋮(n−2)
7 ⋮ n-2
Nên (n-2) ϵ {-1; 1; -7; 7}
Vậy n ϵ {1; 3; -5; 9}