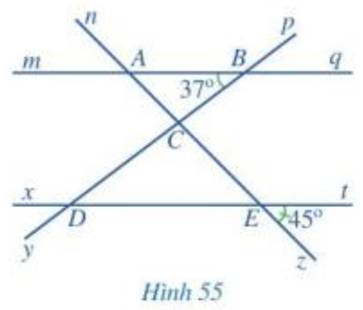
Thay 37 độ=39 độ nhoa
A, Kể tên các góc đồng vị bằng nhau
b, kể tên các góc so le trong bằng nhau
c, Tính góc BAC, CDE
d, Tính góc BCE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Các góc đồng vị bằng nhau là:
\(\widehat{nAm}\) = \(\widehat{AEx}\); \(\widehat{mAE}\) = \(\widehat{zED}\); \(\widehat{nAB}\) = \(\widehat{AEt}\)
\(\widehat{qAE}\) = \(\widehat{tEz}\); \(\widehat{pBq}\) = \(\widehat{BDE}\); \(\widehat{qBC}\) = \(\widehat{EDy}\); \(\widehat{pBA}\) = \(\widehat{BDx}\); \(\widehat{ABD}\)=\(\widehat{xDy}\)
b, Các góc so le trong:
\(\widehat{ABC}\) = \(\widehat{CDE}\); \(\widehat{mAC}\) = \(\widehat{CEt}\); \(\widehat{BAC}\) = \(\widehat{CED}\); \(\widehat{qBc}\) = \(\widehat{CDx}\)
c, \(\widehat{BAC}\) = \(\widehat{zEt}\) = 450
\(\widehat{CDE}\) = \(\widehat{ABC}\) = 390
d, \(\widehat{BCE}\) = \(\widehat{CDE}\) + \(\widehat{CED}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó.
\(\widehat{CED}\) = \(\widehat{zEt}\) = 450 (hai góc đối đỉnh)
\(\widehat{BCE}\) = 390 + 450 = 840

Bài 1:
a) \(3^7:3^5-\left(\dfrac{5}{17}\right)^0=3^{7-5}-1=3^2-1=9-1=8\)
b) \(\left(\dfrac{5}{2}\right)^{13}:\left(\dfrac{1}{2}+2\right)^3\)
\(=\left(\dfrac{5}{2}\right)^{13}:\left(\dfrac{5}{2}\right)^3\)
\(=\left(\dfrac{5}{2}\right)^{10}\)
c) \(8.\left(\dfrac{1}{4}\right)^3+\left(\dfrac{2}{27}\right)^0-\dfrac{1}{8}\)
\(=8.\dfrac{1}{64}+1-\dfrac{1}{8}\)
\(=\dfrac{1}{8}+1-\dfrac{1}{8}\)
\(=1\)
Bài 2:
a) \(\dfrac{3^4.4^4}{6^4}=\dfrac{3^4.\left(2^2\right)^4}{\left(2.3\right)^4}=\dfrac{3^4.2^8}{2^4.3^4}=\dfrac{2^8}{2^4}=2^4=16\)
b) \(\dfrac{15^3}{10^3}=\dfrac{\left(3.5\right)^3}{ \left(2.5\right)^3}=\dfrac{3^3.5^3}{2^3.5^3}=3^3:2^3=\dfrac{27}{8}\)
c) \(\dfrac{4^2.12^5}{9^2.2^{10}}=\dfrac{\left(2^2\right)^2.\left[3.\left(2^2\right)\right]^5}{\left(3^2\right)^2.2^{10}}=\dfrac{2^4.3^5.2^{10}}{3^4.2^{10}}=2^4.3=16.3=48\)
d) \(\dfrac{6^2+5.2^2+4}{15}=\dfrac{\left(2.3\right)^2+5.2^2+2^2}{15}=\dfrac{2^2.3^2+5.2^2+2^2}{15}=\dfrac{2^2\left(3^2+5+1\right)}{15}=\dfrac{2^2.15}{15}=2^2=4\)
Bài 3:
a) \(\dfrac{\left(\dfrac{2}{3}\right)^3.\left(\dfrac{-3}{4}\right)^2.\left(-1\right)^5}{\left(\dfrac{2}{5}\right)^2.\left(\dfrac{-5}{12}\right)^2}\)
\(=\dfrac{\left(\dfrac{2}{3}\right)^3.\left(\dfrac{-3}{4}\right)^2.-1}{\left[\dfrac{2}{5}.\left(\dfrac{-5}{12}\right)\right]^2}\)
\(=\dfrac{\left(\dfrac{2}{3}\right)^3. \left(\dfrac{-3}{4}\right)^2.-1}{\left(\dfrac{-1}{6}\right)^2}\)
\(=\left(\dfrac{2}{3}\right)^3.\left[\left(\dfrac{-3}{4}\right).-6\right]^2.-1\)
\(=\left(\dfrac{2}{3}\right)^3.\left(\dfrac{9}{2}\right)^2.-1\)
\(=\left(\dfrac{2}{3}\right)^2.\dfrac{2}{3}.\left(\dfrac{9}{2}\right)^2.-1\)
\(=\left(\dfrac{2}{3}.\dfrac{9}{2}\right)^2.\dfrac{2}{3}.-1\)
\(=9.\dfrac{2}{3}.-1\)
\(=6.-1=-6\)
b) \(\dfrac{6^6+6^3.3^3+3^6}{-73}=\dfrac{\left(2.3\right)^6+\left(2.3\right)^3.3^3+3^6}{-73}=\dfrac{2^6.3^6+2^3.3^3.3^3+3^6}{-73}=\dfrac{2^6.3^6+2^3.3^6+3^6}{-73}=\dfrac{3^6\left(2^6+2^3+1\right)}{-73}=\dfrac{3^6.73}{-73}=\dfrac{3^6}{-1}=\left(-3\right)^6\)
\(#Wendy.Dang\)
Lần sau bnn gửi từng bài thôi nha, chứ như vầy nhiều quá thì làm không nổi mất. đánh máy nãy giờ lú luôn gòi nè :))

a) \(5^6:5^5+\left(\dfrac{4}{9}\right)^0=5^{6-5}+1=5+1=6\)
b) \(\left(\dfrac{3}{7}\right)^{21}:\left(1-\dfrac{40}{49}\right)^3\)
\(=\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{9}{49}\right)^3\)
\(=\left(\dfrac{3}{7}\right)^{21}:\left[\left(\dfrac{3}{7}\right)^2\right]^3\)
\(=\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{3}{7}\right)^6\)
\(=\left(\dfrac{3}{7}\right)^{21-6}=\left(\dfrac{3}{7}\right)^{15}\)
c) \(\left(\dfrac{2}{3}\right)^3-\left(\dfrac{-52}{3}\right)^0+\dfrac{4}{9}\)
\(=\dfrac{8}{27}-1+\dfrac{4}{9}\)
\(=\dfrac{8-27+12}{27}=-\dfrac{7}{27}\)
\(a)5^6:5^5+\left(\dfrac{4}{9}\right)^0=5^1+1=6\)
\(b,\left(\dfrac{3}{7}\right)^{21}:\left(1-\dfrac{40}{49}\right)^3\)
\(=\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{49-40}{49}\right)^3\)
\(=\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{9}{49}\right)^3=\left(\dfrac{3}{7}\right)^{21}:[\left(\dfrac{3}{7}\right)^2]^3\)
\(=\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{3}{7}\right)^6=\left(\dfrac{3}{7}\right)^{21-6}\)
\(=\left(\dfrac{3}{7}\right)^{15}\)
\(c,3.\left(\dfrac{2}{3}\right)^3-\left(\dfrac{-52}{3}\right)^0+\dfrac{4}{9}\)
\(=3.\dfrac{8}{27}-1+\dfrac{4}{9}\)
\(=\dfrac{8}{9}-1+\dfrac{4}{9}\)
\(=\dfrac{8-9+4}{9}=\dfrac{1}{3}\)

Thể tích bể bơi là: 12 x 10 x 1,2 = 144 (m3)
Gọi lượng nước mà mỗi máy bơm cần bơm vào bể lần lượt là:
\(x;y;z\) (m3); \(x;y;z>0\)
Theo bài ra ta có: \(\dfrac{x}{7}=\dfrac{y}{8}=\dfrac{z}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{7}=\dfrac{y}{8}=\dfrac{z}{9}\) = \(\dfrac{x+y+z}{7+8+9}\) = \(\dfrac{144}{24}\) = 6
\(x\) = 6 x 7 = 42
y = 6 x 8 = 48
z = 6 x 9 = 54
Kết luận lượng nước mà mỗi máy cần bơm để hồ đầy theo thứ tự lần lượt là:
42 m3; 48 m3; 54 m3
Thể tích bể:
12 . 10 . 1,2 = 144 (m³)
Gọi x (m³), y (m³), z (m³) lần lượt là số m³ mà máy bơm thứ nhất, máy bơm thứ hai và máy bơm thứ ba phải bơm (x, y, z > 0)
Ta có: x + y + z = 144 (m³)
Do lượng nước bơm được của ba máy tỉ lệ với 7; 8; 9 nên:
x/7 = y/8 = z/9
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/7 = y/8 = z/9 = (x + y + z)/(7 + 8 + 9) = 144/24 = 6
x/7 = 6 ⇒ x = 7.6 = 42 (nhận)
y/8 = 6 ⇒ y = 8.6 = 48 (nhận)
z/9 = 6 ⇒ z = 9.6 = 54 (nhận)
Vậy số m³ nước ba máy bơm để đầy bể lần lượt là: 42 m³, 48 m³, 54 m³

Thể tích bể:
12 . 10 . 1,2 = 144 (m³)
Gọi x (m³), y (m³), z (m³) lần lượt là số m³ mà máy bơm thứ nhất, máy bơm thứ hai và máy bơm thứ ba phải bơm (x, y, z > 0)
Ta có: x + y + z = 144 (m³)
Do lượng nước bơm được của ba máy tỉ lệ với 7; 8; 9 nên:
x/7 = y/8 = z/9
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/7 = y/8 = z/9 = (x + y + z)/(7 + 8 + 9) = 144/24 = 6
x/7 = 6 ⇒ x = 7.6 = 42 (nhận)
y/8 = 6 ⇒ y = 8.6 = 48 (nhận)
z/9 = 6 ⇒ z = 9.6 = 54 (nhận)
Vậy số m³ nước ba máy bơm để đầy bể lần lượt là: 42 m³, 48 m³, 54 m³

Gọi \(x;y;z\left(x;y;z>0\right)\) lần lượt là lượng nước của 3 máy bơm
Thể tích bể là : \(12.10.1,2=144\left(m^3\right)\)
Theo đề ta có :
\(\dfrac{x}{7}=\dfrac{y}{8}=\dfrac{z}{9}=\dfrac{x+y+z}{7+8+9}=\dfrac{144}{24}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=7.6=42\\y=8.6=48\\z=9.6=54\end{matrix}\right.\)
Vậy mỗi máy lần lượt cần bơm để đầy bể
\(144-42=102m^3\)
\(144-48=96m^3\)
\(144-54=90m^3\)

\(\dfrac{8}{7}:\left(\dfrac{2}{9}-\dfrac{1}{18}\right)+\dfrac{7}{8}:\left(\dfrac{1}{36}-\dfrac{5}{12}\right)\)
\(=\dfrac{8}{7}:\left(\dfrac{4}{18}-\dfrac{1}{18}\right)+\dfrac{7}{8}:\left(\dfrac{1}{36}-\dfrac{15}{36}\right)\)
\(=\dfrac{8}{7}:\dfrac{1}{6}+\dfrac{7}{8}:\dfrac{-7}{18}\)
\(=\dfrac{8}{7}.6+\dfrac{7}{8}.\dfrac{-18}{7}\)
\(=\dfrac{129}{28}\)

\(Z=\dfrac{3a+4}{a+2}=\dfrac{3\left(a+2\right)-2}{a+2}=3-\dfrac{2}{a+2}\)
Vì \(3\inℤ\) nên để \(Z\inℤ\) thì \(\dfrac{2}{a+2}\inℤ\) hay \(a+2\inƯ\left(2\right)\)
\(\Rightarrow a+2\in\left\{\pm1;\pm2\right\}\) \(\Rightarrow a\in\left\{-3;-1;-4;0\right\}\)
Vậy để \(Z\inℤ\) thì \(a\in\left\{-4;-3;-1;0\right\}\)
Để Z là số nguyên : \(\Leftrightarrow\dfrac{3a+4}{a+2}\in Z\)
Xét \(Z=\dfrac{3a+4}{a+2}\)
\(Z=\dfrac{3a+6-2}{a+2}\)
\(Z=\dfrac{3a+6}{a+2}-\dfrac{2}{a+2}=3-\dfrac{2}{a+2}\)
Để \(Z\) là số nguyên :
\(\Leftrightarrow\dfrac{2}{a+2}\in Z\Leftrightarrow\left(a+2\right)\inƯ\left(2\right)\)
Do đó : ta có bảng
| a+2 | 1 | -1 | 2 | -2 |
| a | -1 | -3 | 0 | -4 |
Vậy............

\(\dfrac{1}{2.4}+\dfrac{1}{4.6}+\dfrac{1}{6.8}+...+\dfrac{1}{40.42}\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+...+\dfrac{1}{40}-\dfrac{1}{42}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{2}-\dfrac{1}{42}\right)\)
\(=\dfrac{1}{2}.\dfrac{10}{21}\)
\(=\dfrac{5}{21}\)
\(#Wendy.Dang\)
\(\dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+\dfrac{1}{6\cdot8}+...+\dfrac{1}{40\cdot42}\)
\(=\dfrac{1}{2}\cdot\left(2\cdot\dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+\dfrac{1}{6\cdot8}+...+\dfrac{1}{40\cdot42}\right)\)
\(=\dfrac{1}{2}\cdot\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{40\cdot42}\right)\)
\(=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-...+\dfrac{1}{40}-\dfrac{1}{42}\right)\)
\(=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{42}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{41}{42}\)
\(=\dfrac{41}{84}\)