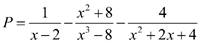
mọi người rút gọn hộ mk nha
Đầy đủ nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LQ
7
12 tháng 8 2022
(2+x).(2-x) = (4-x2)
* hằng đẵng thức đáng nhớ
12 tháng 8 2022
ý mk là nhân hai cái với nhau chứ ai cũng bt là = (4-x^2) rồi.
giống kiểu (2+x).(2+x)=4+2x+2x+x^2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 8 2022
\(\dfrac{3}{5}\)a3b x (10ab3 - \(\dfrac{5}{3}\)b2 + \(\dfrac{5}{6}\)ab)
=\(\dfrac{3}{5}\)a3b . 10ab3 - \(\dfrac{3}{5}\)a3b. \(\dfrac{5}{3}\)b2 + \(\dfrac{3}{5}\)a3b . \(\dfrac{5}{6}\)ab
= 6a4b4 - a3b3 + \(\dfrac{1}{2}\) a4b2
Q
Cho hình chóp cụt tam giác đều có cạnh ở hai đáy lần lượt là 2cm và 3cm, đường cao của mặt bên bằng độ dài đường trung bình của mặt bên. Diện tích xung quanh của hình chóp cụt đó là...
Đọc tiếp
Cho hình chóp cụt tam giác đều có cạnh ở hai đáy lần lượt là 2cm và 3cm, đường cao của mặt bên bằng độ dài đường trung bình của mặt bên. Diện tích xung quanh của hình chóp cụt đó là ...............cm2
#Hỏi cộng đồng OLM #Toán lớp 8
0
NN
2
AH
Akai Haruma
Giáo viên
12 tháng 8 2022
Lời giải:
$C=(m+n)^3-m^2-2mn-n^2=(m+n)^3-(m^2+2mn+n^2)$
$=(m+n)^3-(m+n)^2=2^3-2^2=8-4=4$
15 tháng 8 2022
\(C=\left(m+n\right)^3-\left(m^2+2mn+n^2\right)=\left(m+n\right)^3-\left(m+n\right)^2\)
Thay vào ta được 8 - 4 = 4
12 tháng 8 2022
đặt:
\(\left\{{}\begin{matrix}S_{ABC}=S^2\\S_{BED}=S_1^2\\S_{CFD}=S_2^2\end{matrix}\right.\)
ta có:
\(ED\) // \(AC\) \(\Rightarrow\Delta BED\sim\Delta BAC\)
\(\Rightarrow\dfrac{S_1^2}{S^2}=\dfrac{BD^2}{BC^2}\Leftrightarrow\dfrac{S_1}{S}=\dfrac{BD}{BC}\)
C/M tương tự:
\(\Rightarrow\dfrac{S_2^2}{S^2}=\dfrac{CD^2}{BC^2}\Leftrightarrow\dfrac{S_2}{S}=\dfrac{CD}{BC}\)
\(\Leftrightarrow\dfrac{BD}{BC}+\dfrac{DC}{BC}=\dfrac{S_1+S_2}{S}\)
\(\Leftrightarrow\dfrac{S_1+S_2}{S}=1\)
\(\Leftrightarrow\left(S_1+S_2\right)^2=S^2\)
\(\Leftrightarrow S^2=\left(\sqrt{100}+\sqrt{16}\right)^2=16^2=256\left(cm^2\right)\)
\(\Leftrightarrow S_{ABC}=256cm^2\)
\(ĐKXĐ:x\ne2\)
\(P=\dfrac{1}{x-2}-\dfrac{x^2+8}{x^3-8}-\dfrac{4}{x^2+2x+4}\)
\(=\dfrac{x^2+2x+4}{\left(x-2\right)\left(x^2+2x+4\right)}-\dfrac{x^2+8}{\left(x-2\right)\left(x^2+2x+4\right)}-\dfrac{4\left(x-2\right)}{x^2+2x+4}\)
\(=\dfrac{x^2+2x+4-x^2-8-4x+8}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{4-2x}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{-2\left(x-2\right)}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=-\dfrac{2}{x^2+2x+4}\)