4/ 9 *11+ 4/ 13 * 15 +... 4/95 * 97 + 4/97 * 99
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`527 + {[2 . (2 . 2^3 + 3^2 + 4^2 - 5^2) + 678^0]^3 : 33^2}`
`= 527 + {[2 . (16 + 9 + 16 - 25) + 1]^3 : 33^2}`
`= 527 + {[2 . (25 + 16 - 25) + 1]^3 : 33^2}`
`= 527 + {[2 . 16 + 1]^3 : 33^2}`
`= 527 + {[32 + 1]^3 : 33^2}`
`= 527 + {33^3 :33^2}`
`= 527 + 33^(3-2)`
`= 527 + 33`
`= 560`

`(42 . 43 + 43 . 57 + 43) - 360 : 4 `
`= 43 . (42 + 57 + 1) - 90`
`= 43 . 100 - 90`
`= 4300 - 90 `
`= 4210`
`372 - 19 . 4 + (981:9-13)`
`= 372 - 76 + (109-13)`
`= 296 + 96`
`= 392`

M là tập hợp các số tự nhiên lẻ không lớn hơn 11
Cách 1: liệt kê
\(M=\left\{1;3;5;7;9;11\right\}\)
Cách 2: chỉ ra tính chất đặt trưng
`M={x=2k+1;k∈N;0<=k<=5}`
Ta có: 13 không có trong tập hợp M
`=>13∉M`
9 có trong tập hợp M
`=>9∈M`

a) `(x+4)(y-1)=13`
Ta có bảng:
| x + 4 | 1 | -1 | 13 | -13 |
| y - 1 | 13 | -13 | 1 | -1 |
| x | -3 | -5 | 9 | -17 |
| y | 14 | -12 | 2 | 0 |
b) `xy-3x+y=20`
`=>(xy-3x)+(y-3)=20-3`
`=>x(y-3)+(y-3)=17`
`=>(y-3)(x+1)=17`
Ta có bảng:
| y - 3 | 17 | -1 | -17 | 1 |
| x + 1 | 1 | -17 | -1 | 17 |
| y | 20 | 2 | -14 | 4 |
| x | 0 | -18 | -2 | 16 |

a) 10 ⋮ (x - 1)
⇒ x - 1 ∈ Ư(10) = {-10; -5; -2; -1; 1; 2; 5; 10}
⇒ x ∈ {-9; -4; -1; 0; 2; 3; 6; 11}
b) x + 5 = x - 2 + 7
Để (x - 5) ⋮ (x - 2) thì 7 ⋮ (x - 2)
⇒ x - 2 ∈ Ư(7) = {-7; -1; 1; 7}
⇒ x ∈ {-5; 1; 3; 9}
c) 3x + 8 = 3x - 3 + 11
= 3(x - 1) + 11
Để (3x + 8) ⋮ (x - 3) thì 11 ⋮ (x - 3)
⇒ x - 3 ∈ Ư(11) = {-11; -1; 1; 11}
⇒ x ∈ {-8; 2; 4; 14}

a) 25 chia hết cho n + 2
=> n + 2 ∈ Ư(25)
=> n + 2 ∈ {1; -1; 5; -5; 25; -25}
=> n ∈ {-1; -3; 3; -7; 23; -27}
b) 2n + 4 chia hết cho n - 1
=> (2n - 2) + 6 chia hết chi n - 1
=> 2(n - 1) + 6 chia hết cho n - 1
=> 6 chia hết cho n - 1
=> n - 1 ∈ Ư(6) = {1; -1; 2; -2; 3; -3; 6; -6}
=> n ∈ {2; 0; 3; -1; 4; -2; 7; -5}
a) 25 ⋮ (n + 2)
⇒ n + 2 ∈ Ư(25) = {-25; -5; -1; 1; 5; 25}
⇒ n ∈ {-27; -7; -3; -1; 3; 23}
b) 2n + 4 = 2n - 2 + 6
= 2(n - 1) + 6
Để (2n + 4) ⋮ (n - 1) thì 6 ⋮ (n - 1)
⇒ n - 1 ∈ Ư(6) = {-6; -3; -2; -1; 1; 2; 3; 6}
⇒ n ∈ {-5; -2; -1; 0; 2; 3; 4; 7}

Bài 11.2
\(a,A=3+3^2+3^3+....+3^{99}\\ =\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+....+\left(3^{97}+3^{98}+3^{99}\right)\\ =3\cdot\left(1+3+9\right)+3^4\cdot\left(1+3+9\right)+...+3^{97}\cdot\left(1+3+9\right)\\ =13\cdot\left(3+3^4+....+3^{97}\right)⋮13\\ b,B=5+5^2+...+5^{50}\\ =\left(5+5^2\right)+\left(5^3+5^4\right)+..+\left(5^{49}+5^{50}\right)\\ =5\cdot\left(1+5\right)+5^3\cdot\left(1+5\right)+....+5^{49}\cdot\left(1+5\right)\\ =6\cdot\left(5+5^3+...+5^{49}\right)⋮6\)
Bài 11.4:
a: \(10⋮x-1\)
=>\(x-1\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
=>\(x\in\left\{2;0;3;-1;6;-4;11;-9\right\}\)
b:
\(x+5⋮x-2\)
=>\(x-2+7⋮x-2\)
=>\(7⋮x-2\)
=>\(x-2\in\left\{1;-1;7;-7\right\}\)
=>\(x\in\left\{3;1;9;-5\right\}\)
c: \(3x+8⋮x-1\)
=>\(3x-3+11⋮x-1\)
=>\(11⋮x-1\)
=>\(x-1\in\left\{1;-1;11;-11\right\}\)
=>\(x\in\left\{2;0;12;-10\right\}\)
Bài 11.5:
a: (x+4)(y-1)=13
=>\(\left(x+4;y-1\right)\in\left\{\left(1;13\right);\left(13;1\right);\left(-1;-13\right);\left(-13;-1\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(-3;14\right);\left(9;2\right);\left(-5;-12\right);\left(-17;0\right)\right\}\)
b: xy-3x+y=20
=>x(y-3)+y-3=17
=>(x+1)(y-3)=17
=>\(\left(x+1;y-3\right)\in\left\{\left(1;17\right);\left(17;1\right);\left(-1;-17\right);\left(-17;-1\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(0;20\right);\left(16;4\right);\left(-2;-14\right);\left(-18;2\right)\right\}\)

`-12(x - 15) + 7(3 - x) = 15`
`=> -12x + 180 + 21 - 7x - 15 = 0`
`=> -19x + 186 = 0`
`=> -19x = -186`
`=> x = -186 : (-19) `
`=> x = 186/19`
Vậy ...
-------------------------
`(x - 1) . (x + 2) . (-x - 3) = 0`
`=> x - 1 = 0` hoặc `x + 2 = 0` hoặc `-x - 3 = 0`
`=> x =1` hoặc `x = -2` hoặc `x = -3`
Vậy ...

\(=-125.75-125.\left(-43\right)+75.125+75.43\)
\(=\left(-125.75+75.125\right)+125.43+75.43\)
\(=0+43.\left(125+75\right)\)
\(=43.200\)
\(=8600\)
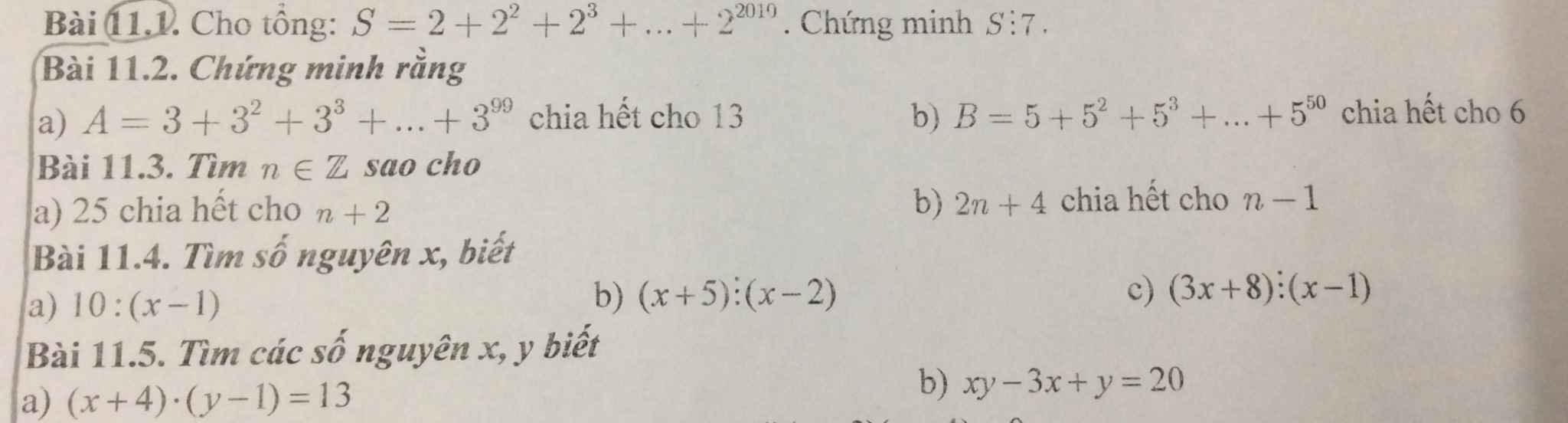
\(\dfrac{4}{9\cdot11}+\dfrac{4}{13\cdot15}+...+\dfrac{4}{95\cdot97}+\dfrac{4}{97\cdot99}\\ =2\cdot\left(\dfrac{2}{9\cdot11}+\dfrac{2}{13\cdot15}+...+\dfrac{2}{95\cdot97}+\dfrac{2}{97\cdot99}\right)\\ =2\left(\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{15}+...+\dfrac{1}{95}-\dfrac{1}{97}+\dfrac{1}{97}-\dfrac{1}{99}\right)\\ =2\cdot\left(\dfrac{1}{9}-\dfrac{1}{99}\right)\\ =2\cdot\dfrac{11-1}{99}\\ =2\cdot\dfrac{10}{99}\\ =\dfrac{20}{99}\)
Sửa đề: `S = 4/(9.11) + 4/(11.13) + ... + 4/(97.99)`
`S = 2 . (2/(9.11) + 2/(11.13) + ... +2/(97.99))`
`S = 2 . (1/9 - 1/11 + 1/11 - 1/13 + ... + 1/97 - 1/99)`
`S = 2 . (1/9 - 1/99)`
`S = 2 . (11/99 - 1/99)`
`S = 2 . 10/99 `
`S = 20/99`