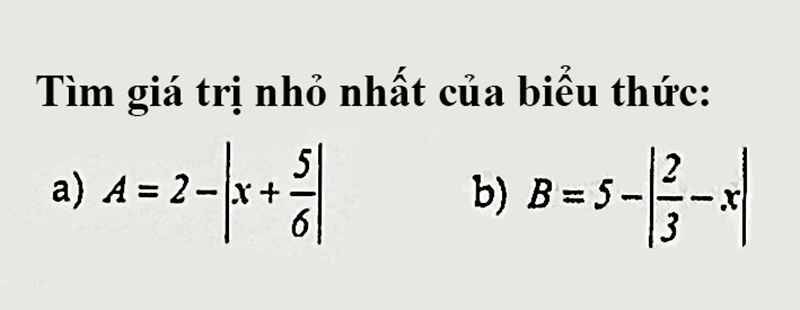Bạn tham khảo.

Ta có ( x - 3 )² + ( y - 4 )² + ( x² - xz )²⁰²⁰ = 0

Vì ( x - 3 )² ≥ 0 với ∀_x

    ( y - 4 )² ≥ 0 với ∀_y

    ( x² - xz )²⁰²⁰ ≥ 0 với ∀_x; ∀_z

⇒ ( x - 3 )² + ( y - 4 )² + ( x² - xz )²⁰²⁰ ≥ 0

Dấu " = " xảy ra khi

\(\left\{{}\begin{matrix}\left(x-3\right)^2=0\\\left(y-4\right)^2=0\\\left(x^2-xz\right)^{2020}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x-3=0\\y-4=0\\x^2-xz=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3\\y=4\\z=3\end{matrix}\right.\)

Vậy x = 3; y = 4; z = 3

em cảm ơn

Ta có A = 10⁵ - 5⁶ = 5⁵( 2⁵ - 5) = 5⁵ . 27 

A ⋮ 27 vì 27 ⋮ 27

Vậy A ⋮ 27

\(A=2-\left|x+\dfrac{5}{6}\right|\\ Mà:\left|x+\dfrac{5}{6}\right|\ge0\forall x\in R\\ Vây:max_A=2.khi.x+\dfrac{5}{6}=0\Leftrightarrow x=-\dfrac{5}{6}\)

B làm tương tự, nhưng mình nghĩ là tìm max chứ min thì cái biểu thực GTTĐ luôn không âm mà như thế thì nhỏ vô tận luôn í

cả hai câu sai đề, A và B không có GTNN

\(\left(3-x\right)^3=-\dfrac{27}{64}\)

\(\left(3-x\right)^3=\left(\dfrac{-3}{4}\right)^3\)

\(=>3-x=\dfrac{-3}{4}\)

\(x=3-\dfrac{-3}{4}=\dfrac{12}{4}+\dfrac{3}{4}\)

\(x=\dfrac{15}{4}\)

________

\(\left(x-5\right)^3=\dfrac{1}{-27}\)

\(\left(x-5\right)^3=\left(\dfrac{-1}{3}\right)^3\)

\(=>x-5=\dfrac{-1}{3}\)

\(x=\dfrac{-1}{3}+5=\dfrac{-1}{3}+\dfrac{15}{3}\)

\(x=\dfrac{14}{3}\)

_____________

\(\left(x-\dfrac{1}{2}\right)^3=\dfrac{27}{8}\)

\(\left(x-\dfrac{1}{2}\right)^3=\left(\dfrac{3}{2}\right)^3\)

\(=>x-\dfrac{1}{2}=\dfrac{3}{2}\)

\(x=\dfrac{3}{2}+\dfrac{1}{2}\)

\(x=2\)

________

\(\left(2x-1\right)^2=\dfrac{1}{4}\)            

\(\left(2x-1\right)^2=\left(\dfrac{1}{2}\right)^2\)           hoặc              \(\left(2x-1\right)^2=\left(\dfrac{-1}{2}\right)^2\)

\(=>2x-1=\dfrac{1}{2}\)                                       \(2x-1=\dfrac{-1}{2}\)

\(2x=\dfrac{1}{2}+1=\dfrac{1}{2}+\dfrac{2}{2}\)                               \(2x=\dfrac{-1}{2}+1=\dfrac{-1}{2}+\dfrac{2}{2}\)

\(2x=\dfrac{3}{2}\)                                                     \(2x=\dfrac{1}{2}\)

\(x=\dfrac{3}{2}:2=\dfrac{3}{2}.\dfrac{1}{2}\)                                     \(x=\dfrac{1}{2}:2=\dfrac{1}{2}.\dfrac{1}{2}\)

\(x=\dfrac{3}{4}\)                                                       \(x=\dfrac{1}{4}\)

____________

\(\left(2-3x\right)^2=\dfrac{9}{4}\)

\(\left(2-3x\right)^2=\left(\dfrac{3}{2}\right)^2\)                hoặc                  \(\left(2-3x\right)^2=\left(\dfrac{-3}{2}\right)^2\)

\(=>2-3x=\dfrac{3}{2}\)                                               \(2-3x=\dfrac{-3}{2}\)

\(3x=2-\dfrac{3}{2}=\dfrac{4}{2}-\dfrac{3}{2}\)                                      \(3x=2-\dfrac{-3}{2}=\dfrac{4}{2}+\dfrac{3}{2}\)

\(3x=\dfrac{1}{2}\)                                                            \(3x=\dfrac{7}{2}\)

\(x=\dfrac{1}{2}.\dfrac{1}{3}\)                                                          \(x=\dfrac{7}{2}.\dfrac{1}{3}\)

\(x=\dfrac{1}{6}\)                                                               \(x=\dfrac{7}{6}\)

______________

\(\left(1-\dfrac{2}{3}\right)^2=\dfrac{4}{9}\) -> Kiểm tra đề câu này

(3-x)^{3_{=(-\(\dfrac{3}{4}\))}3}

^{3-x=-\(\dfrac{3}{4}\)}

  ^{x=3-(-\(\dfrac{3}{4}\))}

  ^{x=\(\dfrac{15}{4}\)}