viết tích \(25^6.8^4\) dưới dạng lũy thừa cơ số 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để biểu thức đã cho đạt giá trị lớn nhất thì (x² - 9)⁴ và -|2x + 6| - (x² - 9)⁴ đạt giá trị lớn nhất
Mà (x² - 9)⁴ ≥ 0 với mọi x ∈ R
⇒ (x² - 9)⁴ = 0 là giá trị nhỏ nhất
⇒ x² - 9 = 0
⇒ x² = 9
⇒ x = 3 hoặc x = -3
*) x = 3
⇒ -|2x + 6| = -12
*) x = -3
⇒ -|2x + 6| = 0
Vậy giá trị lớn nhất của biểu thức đã cho là 2023 khi x = -3



Vì \(\left|x+2\right|+\left|x+\dfrac{3}{5}\right|+\left|x+\dfrac{1}{2}\right|>0\) nên \(4x>0\) hay \(x>0\)
\(\Rightarrow x+2+x+\dfrac{3}{5}+x+\dfrac{1}{2}=4x\)
\(3x+2+\dfrac{3}{5}+\dfrac{1}{2}=4x\)
\(3x+\dfrac{31}{10}=4x\)
\(\Rightarrow4x-3x=\dfrac{31}{10}\)
\(\Rightarrow x=\dfrac{31}{10}\)
Lời giải:
Vì $|x+2|+|x+\frac{3}{5}|+|x+\frac{1}{2}|\geq 0$ với mọi $x$
$\Rightarrow 4x\geq 0\Rightarrow x\geq 0$.
Khi đó:
$x+2>0; x+\frac{3}{5}>0; x+\frac{1}{2}>0$
$\Rightarrow |x+2|+|x+\frac{3}{5}|+|x+\frac{1}{2}|=4x$
$\Rightarrow x+2+x+\frac{3}{5}+x+\frac{1}{2}=4x$
$\Rightarrow 3x+\frac{31}{10}=4x$
$\Rightarrow x=\frac{31}{10}$ (tm)


Lời giải:
$G=\frac{2x^2+15}{x^2+3}=\frac{2(x^2+3)+9}{x^2+3}=2+\frac{9}{x^2+3}$
Vì $x^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow x^2+3\geq 3$
$\Rightarrow \frac{9}{x^2+3}\leq 3$
$\Rightarrow G=2+\frac{9}{x^2+3}\leq 2+3=5$.
Vậy $G_{\max}=5$. Giá trị này đạt được khi $x=0$
Biểu thức này không có giá trị min bạn nhé.

\(\dfrac{6}{5}\sqrt{1\dfrac{9}{16}}-\left(-\dfrac{3}{4}\right)^2:0,25\)
\(=\dfrac{6}{5}\cdot\sqrt{\dfrac{25}{16}}-\dfrac{9}{16}:0,25\)
\(=\dfrac{6}{5}\cdot\sqrt{\left(\dfrac{5}{4}\right)^2}-\dfrac{9}{16}:\dfrac{1}{4}\)
\(=\dfrac{6}{5}\cdot\dfrac{5}{4}-\dfrac{9\cdot4}{16}\)
\(=\dfrac{6}{4}-\dfrac{9}{4}\)
\(=\dfrac{6-9}{4}\)
\(=-\dfrac{3}{4}\)

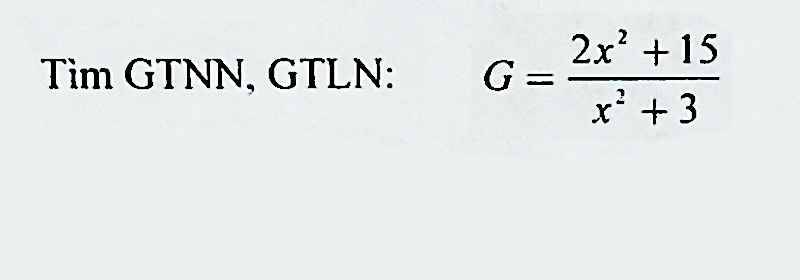
\(25^6\cdot8^4\)
\(=\left(5^2\right)^6\cdot\left(2^3\right)^4\)
\(=5^{2\cdot6}\cdot2^{3\cdot4}\)
\(=5^{12}\cdot2^{12}\)
\(=\left(5\cdot2\right)^{12}\)
\(=10^{12}\)
\(25^6.8^4\)
\(=\left(5^2\right)^6.\left(2^3\right)^4\)
\(=5^{2.6}.2^{3.4}\)
\(=5^{12}.2^{12}\)
\(=\left(5.2\right)^{12}\)
\(=10^{12}\)