\(f\left(1\right)\cdot f\left(-2\right)\)

\(=\left(a+b+c\right)\left(4a-2b+c\right)\)

\(=\left(a+11a+5c+c\right)\left(4a-22a-10c+c\right)\)

\(=\left(12a+6c\right)\left(-18a-9c\right)\)

\(=6\left(2a+c\right)\cdot\left(-9\right)\left(2a+c\right)\)

\(=-54\left(2a+c\right)^2< =0\)(luôn đúng)

$f\left(1\right)\cdot f\left(-2\right)$

$=\left(a+b+c\right)\left(4a-2b+c\right)$

$=\left(a+11a+5c+c\right)\left(4a-22a-10c+c\right)$

$=\left(12a+6c\right)\left(-18a-9c\right)$

$=6\left(2a+c\right)\cdot \left(-9\right)\left(2a+c\right)$

=−54(2�+�)2<=0=−54(2a+c)2<=0

a: Xét ΔMAB và ΔMCD có

MA=MC

���^=���^AMB=CMD(hai góc đối đỉnh)

MB=MD

Do đó: ΔMAB=ΔMCD

b: Xét ΔCBD có

CM,DN là các đường trung tuyến

CM cắt DN tại G

Do đó: G là trọng tâm của ΔCBD

tick đê!

c: 

ΔABM=ΔCDM

=>AB=CD

Xét ΔBCD có BD-BC<CD

=>\(2\left(BM-BN\right)< AB\)

=>\(BM-BN< \dfrac{1}{2}BA\)

a. Đổi 10 phút =1/6 giờ và 20 phút =1/3 giờ

Quãng đường người đó đi từ nhà đến bến xe buýt là: \(\dfrac{1}{6}.x=\dfrac{x}{6}\left(km\right)\)

Quãng đường người đó đi từ bến xe buýt đến nơi làm việc là: \(\dfrac{1}{3}.y=\dfrac{y}{3}\left(km\right)\)

Quãng đường người đó đi từ nhà đến nơi làm việc là:

\(s=\dfrac{x}{6}+\dfrac{y}{3}\)

b.

Chiều rộng của hình chữ nhật là: \(a-2\left(cm\right)\)

Diện tích hình chữ nhật là:

\(S=a\left(a-2\right)=a^2-2a\left(cm^2\right)\)

c.

Thay \(x=2\) vào Q(x) ta được:

\(Q\left(2\right)=2^2+2-6=4+2-6=0\)

\(\Rightarrow x=2\) là nghiệm của đa thức \(Q\left(x\right)\)

a: 10p=1/6 giờ; 20p=1/3 giờ

Độ dài quãng đường người đó đi từ nhà đến bến xe buýt là \(\dfrac{1}{6}x\left(km\right)\)

Độ dài quãng đường người đó đi xe buýt là \(\dfrac{1}{3}y\left(km\right)\)

Tổng độ dài quãng đường là: \(\dfrac{1}{6}x+\dfrac{1}{3}y\left(km\right)\)

b: Chiều rộng là a-2(cm)

Diện tích hình chữ nhật là \(a\left(a-2\right)=a^2-2a\left(cm^2\right)\)

c: \(Q\left(2\right)=2^2+2-6=4+2-6=0\)

=>x=2 là nghiệm của Q(x)

a: \(AM=MB=\dfrac{AB}{2}\)

\(AN=NC=\dfrac{AC}{2}\)

mà AB=AC

nên AM=MB=AN=NC

O nằm trên đường trung trực của AB

=>OA=OB(1)

O nằm trên đường trung trực của AC

=>OA=OC(2)

Từ (1),(2) suy ra OA=OB=OC

Vì M là trung điểm của AB và O nằm trên đường trung trực của AB

nên OM\(\perp\)AB tại M

Vì N là trung điểm của AC và O nằm trên đường trung trực của AC

nên ON\(\perp\)AC tại N

Xét ΔAMO vuông tại M và ΔANO vuông tại N có

AM=AN

AO chung

Do đó: ΔAMO=ΔANO

b: I nằm trên đường trung trực của OB

=>IO=IB(3)

Ta có: I nằm trên đường trung trực của OC

=>IO=IC(4)

Từ (3),(4) suy ra IB=IC

=>I nằm trên đường trung trực của BC(5)

Ta có: OB=OC

=>O nằm trên đường trung trực của BC(6)

Ta có:AB=AC

=>A nằm trên đường trung trực của BC(7)

Từ (5),(6),(7) suy ra A,O,I thẳng hàng

a: Dữ liệu định tính là số cân nặng

Dữ liệu định lượng là số người

b: Số cân nặng lớn nhất là 45kg

Số cân nặng nhỏ nhất là 28kg

Số người nặng 31kg là 5 người

a: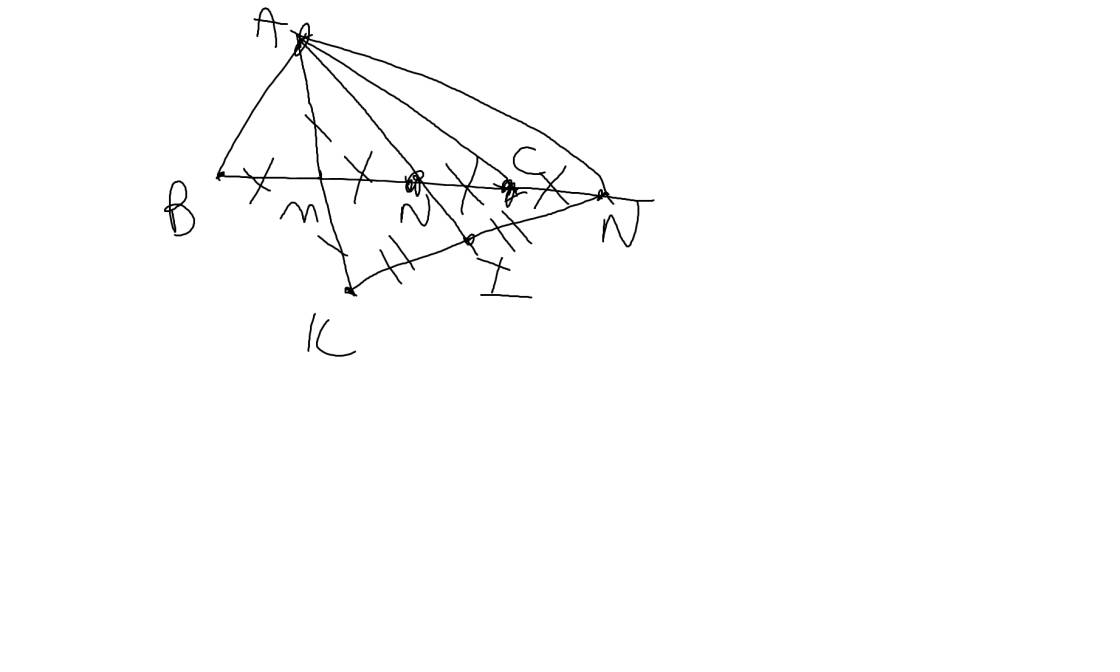 

b: BM=MN=NC

mà NC=CP

nên BM=MN=NC=CP

=>PN=2/3PM

Ta có: MA=MK

mà M nằm giữa A và K

nên M là trung điểm của AK

Xét ΔPAK có

PM là đường trung tuyến

\(PN=\dfrac{2}{3}PM\)

Do đó: N là trọng tâm của ΔPAK

c: Xét ΔAKP có

I là trung điểm của KP

N là trọng tâm

Do đó: A,I,N thẳng hàng

\(\left(x-3\right)+\left(x-4\right)\left(x+4\right)-\left(2x-1\right)\)

\(=x-3+x^2-16-2x+1\)

\(=x^2-x-18\)

\(\left(x-3\right)+\left(x-4\right).\left(x+4\right)-\left(2x-1\right)\)

\(=x-3+x.x+4x-4x+16-2x+1\)

\(=x-3+x^2-16-2x+1\)

\(=x^2+\left(x-2x\right)+\left(-3-16+1\right)\)

\(=x^2-x-18\)

báo cáo cho các bạn ấy chừa tội còn đăng lung tung trên diễn đàn

Bọn nó nhờn lắm bà ơi..