(1/2xy^2+x^2-x^2y)-M=-xy^2+x^2y+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



(x+2)(y-1)=133
=>\(\left(x+2;y-1\right)\in\left\{\left(1;133\right);\left(133;1\right);\left(-1;-133\right);\left(-133;-1\right);\left(7;19\right);\left(19;7\right);\left(-7;-19\right);\left(-19;-7\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(-1;144\right);\left(131;2\right);\left(-3;-132\right);\left(-135;0\right);\left(5;20\right);\left(17;8\right);\left(-9;-18\right);\left(-21;-6\right)\right\}\)
b: (x-5)(y-2)=21
=>\(\left(x-5;y-2\right)\in\){(1;21);(21;1);(-1;-21);(-21;-1);(3;7);(7;3);(-3;-7);(-7;-3)}
=>\(\left(x;y\right)\in\){(6;23);(26;3);(4;-19);(-16;1);(8;9);(12;5);(2;-5);(-2;-1)}

a: D đối xứng H qua AB
=>AH=AD;BH=BD
E đối xứng H qua AC
=>AH=AE; CH=CE
Xét ΔAHB và ΔADB có
AH=AD
HB=DB
AB chung
Do đó: ΔAHB=ΔADB
=>\(\widehat{AHB}=\widehat{ADB}=90^0\)
ΔAHB=ΔADB
=>\(\widehat{HAB}=\widehat{DAB}\)
=>AB là phân giác của góc HAD
Xét ΔAHC và ΔAEC có
AH=AE
CH=CE
AC chung
Do đó: ΔAHC=ΔAEC
=>\(\widehat{AHC}=\widehat{AEC}=90^0\)
ΔAHC=ΔAEC
=>\(\widehat{HAC}=\widehat{EAC}\)
=>AC là phân giác của góc HAE
\(\widehat{DAE}=\widehat{DAH}+\widehat{EAH}=2\left(\widehat{BAH}+\widehat{CAH}\right)=2\cdot90^0=180^0\)
=>D,A,E thẳng hàng
=>BD//CE
Xét tứ giác BDEC có BD//EC
nên BDEC là hình thang
b: Ta có: AD=AH
AH=AE
Do đó: AD=AE
=>A là trung điểm của DE
Xét ΔABC vuông tại A có AH là đường cao
nên \(HB\cdot HC=HA^2\)
=>\(BD\cdot CE=\left(\dfrac{1}{2}DE\right)^2=\left(\dfrac{DE}{2}\right)^2\)
c: Xét ΔABC vuông tại A có AH là đường cao
nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
=>\(\dfrac{1}{AH^2}=\dfrac{1}{3^2}+\dfrac{1}{4^2}=\dfrac{25}{144}\)
=>\(AH=\sqrt{\dfrac{144}{25}}=\dfrac{12}{5}=2,4\left(cm\right)\)
=>DE=2AH=4,8(cm)

(x+3)+(x+6)+...+(x+51)=493
=>17x+(3+6+...+51)=493
=>\(17x+3\left(1+2+...+17\right)=493\)
=>\(17x+3\cdot17\cdot\dfrac{18}{2}=493\)
=>\(17x+51\cdot9=493\)
=>17x=34
=>x=2

Vận tốc của ô tô là:
`3 : 1 = 3 (km/h)`
Đáp số: `3km/h`
---------------------
Quãng đường = Vận tốc x thời gian

\(\dfrac{2024}{1011}>\dfrac{2022}{1011}=2;2=\dfrac{200}{100}>\dfrac{199}{100}\)
Do đó: \(\dfrac{2024}{1011}>\dfrac{199}{100}\)
\(\dfrac{2024}{1011}=\dfrac{2022}{1011}+\dfrac{2}{1011}=2+\dfrac{2}{1011}>2\)
\(\dfrac{199}{100}=\dfrac{200}{100}-\dfrac{1}{100}=2-\dfrac{1}{100}< 2\)
=> \(\dfrac{199}{100}< 2< \dfrac{2024}{1011}\)
Hay \(\dfrac{199}{100}< \dfrac{2024}{1011}\)

Hiệu của số thứ 2 mới và số thứ 2 cũ bằng hiệu giữa tổng mới và tổng cũ
Hiệu của số thứ 2 mới và số thứ 2 cũ là:
`580 - 420 = 160 `
Ta có sơ đồ:
Số thứ 2 cũ: `1` phần
Số thứu 2 mới: `3` phần
Hiệu số phần bằng nhau là:
`3 - 1 = 2` (phần)
Giá trị 1 phần là:
`160 : 2 = 80`
Số thứ hai cũ là:
`80 ` x `1 = 80`
Số thứ nhất là:
`420 - 80 = 340`
Đáp số: .....
2 lần số thứ hai là 580-420=160
Số thứ hai là 160:2=80
Số thứ nhất là 420-80=340

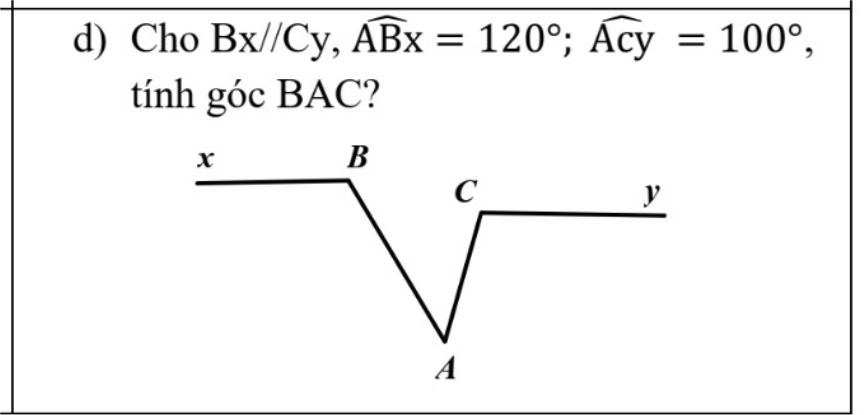
Gọi F là giao điểm của Cy với AB
Bx//Cy
=>\(\widehat{BFC}=\widehat{xBC}\)(hai góc so le trong)
=>\(\widehat{BFC}=120^0\)
Ta có: \(\widehat{BFC}+\widehat{AFC}=180^0\)(hai góc kề bù)
=>\(\widehat{AFC}+120^0=180^0\)
=>\(\widehat{AFC}=60^0\)
Ta có: \(\widehat{ACF}+\widehat{ACy}=180^0\)(hai góc kề bù)
=>\(\widehat{ACF}+100^0=180^0\)
=>\(\widehat{ACF}=80^0\)
Xét ΔACF có \(\widehat{AFC}+\widehat{ACF}+\widehat{CAF}=180^0\)
=>\(\widehat{BAC}=180^0-60^0-80^0=40^0\)
\(\left(\dfrac{1}{2}xy^2+x^2-x^2y\right)-M=-xy^2+x^2y+1\)
=>\(M=\dfrac{1}{2}xy^2+x^2-x^2y+xy^2-x^2y-1\)
=>\(M=\dfrac{3}{2}xy^2+x^2-2x^2y-1\)
M= xy^2+x^y1-(1/2xy^2+x^2-x^2y)
M=xy^2+x^2y+1-1/2xy^2-x^2+x^2y
M=1/2xy^2+2x^2y-x^2-1