tìm 3 số tự nhiên liên tiếp cho biết tích của 2 số cuối lớn hơn tích của 2 số đầu 12 đơn vi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 9:
a,Gọi độ dài cạnh góc vuông là: a
Theo pytago ta có: a2 + a2 = 22 = 4 ⇒ 2a2 = 4 ⇒ a2 = 2 ⇒ a = \(\sqrt{2}\)
b, Gọi độ dài cạnh góc vuông là :b
Theo pytago ta có:
b2 + b2 = 102 =100 ⇒ 2b2 = 100 ⇒ b2 = 50⇒ b = 5\(\sqrt{2}\)
Bài 8 cô làm rồi nhé.
Bài 10 ; Gọi độ dài các cạnh góc của tam giác vuông lần lượt là:
a; b theo bài ra ta có:
\(\dfrac{a}{5}\) = \(\dfrac{b}{12}\) \(\Rightarrow\) \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{a^2+b^2}{25+144}\) (1)
Theo pytago ta có: a2 + b2 = 522 = 2704 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{2704}{169}\) = 16
⇒ a2 = 25.16 = (4.5)2 ⇒ a = 20
b2 = 144.16 = (12.4)2 ⇒ b = 48

A B C
Giả sử \(\dfrac{AB}{AC}=\dfrac{5}{12}\Rightarrow AB=\dfrac{5.AC}{12}\) (1)
Ta có
\(AC^2=BC^2-AB^2\) (Pitago)
\(\Rightarrow AC^2=26^2-\left(\dfrac{5.AC}{12}\right)^2=576\Rightarrow AC=24\) cm Thay vào (1)
\(\Rightarrow AB=\dfrac{5.24}{12}=10cm\)
\(b:c=5:12\Rightarrow\dfrac{b}{5}=\dfrac{c}{12}\Rightarrow\dfrac{b^2}{25}=\dfrac{c^2}{144}=\dfrac{a^2}{25+144}=\dfrac{a^2}{169}=\dfrac{26^2}{169}=\dfrac{26^2}{13^2}\)
\(\Rightarrow b^2=25.\dfrac{26^2}{13^2}\Rightarrow b=5.\dfrac{26}{13^{ }}=10\left(cm\right)\)
\(\Rightarrow c=\dfrac{12}{5}.10=24\left(cm\right)\)

A B C D E G
Đề bài phải sửa thành AE=ED
a/
Xét tg ABC
DE//AB (gt)
BD=CD (gt)
=> AE=CE (trong tg đường thẳng đi qua trung điểm 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại) (1)
Mà DE=AE (gt) (2)
Từ (1) và (2) => DE=AE=CE (3)
Ta có
BD=CD (gt); AE=CE (cmt) => DE là đường trung bình của tg ABC
\(\Rightarrow DE=\dfrac{AB}{2}\) (4)
Từ (3) và (4) \(\Rightarrow DE=AE=CE=\dfrac{AB}{2}\)
\(\Rightarrow AE+CE=AB\) Mà \(AE+CE=AC\Rightarrow AB=AC\)
=> tg ABC cân tại A
b/
Xét tg ABC có
AD là trung tuyến (gt)
AE=CE (cmt) => BE là trung tuyến
=> G là trọng tâm của tg ABC (Trong tg 3 đường trung tuyến đồng quy tại 1 điểm gọi là trọng tâm của tg)

a) Xét Δ ABD và Δ ACE ta có :
AB=AC (đề bài)
Góc A chung
Góc AEC = Góc ABD (BD \(\perp\) AC và CE \(\perp\) AB)
⇒ Δ ABD = Δ ACE (góc, cạnh,góc)
b) Ta có : Δ ABD = Δ ACE (cmt)
⇒ AE=AD
⇒ Δ AED cân tại A
d) vì BD \(\perp\) AC và CE \(\perp\) AB
⇒ Δ ECB và Δ DKC là 2 Δ vuông tại E và D (1)
Ta lại có :BD=EC (Δ ABD = Δ ACE)
mà BD=DK (đề bài)
⇒ EC=DK (2)
AB=AC (Δ ABC cân tại A)
mà AE=AD (cmt) và BE=AB-AE; CD=AC-AD
⇒ CD=BE (3)
Từ (1). (2), (3) ⇒ Δ ECB = Δ DKC (cạnh, góc, cạnh)
Câu c không thấy điểm H đề bài cho bạn xem lại


Lời giải:
$A=(x-1)(x-2)(x-3)(x-4)=[(x-1)(x-4)][(x-2)(x-3)]=(x^2-5x+4)(x^2-5x+6)$
$=a(a+2)$ (đặt $x^2-5x+4=a$)
$=a^2+2a=(a+1)^2-1=(x^2-5x+5)^2-1\geq -1$
Vậy $S_{\min}=-1$. Giá trị này đạt tại $x^2-5x+5=0$
$\Leftrightarrow x=\frac{5\pm \sqrt{5}}{2}$

\(A=x^2-xy+y^2\)
\(\Rightarrow A=x^2-xy+\dfrac{1}{4}y^2-\dfrac{1}{4}y^2+y^2\)
\(\Rightarrow A=\left(x-\dfrac{1}{2}y\right)^2+\dfrac{3}{4}y^2\)
mà \(\left(x-\dfrac{1}{2}y\right)^2\ge0;\dfrac{3}{4}y^2\ge0\)
\(\Rightarrow A=\left(x-\dfrac{1}{2}y\right)^2+\dfrac{3}{4}y^2\ge0\)
\(\Rightarrow\left(x-\dfrac{1}{2}y\right)^2+\dfrac{3}{4}y^2>0\) với mọi x,y không đồng thời bằng 0
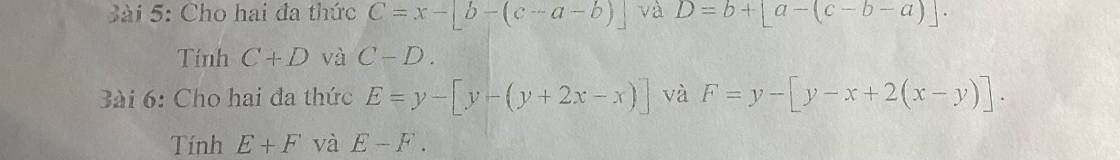
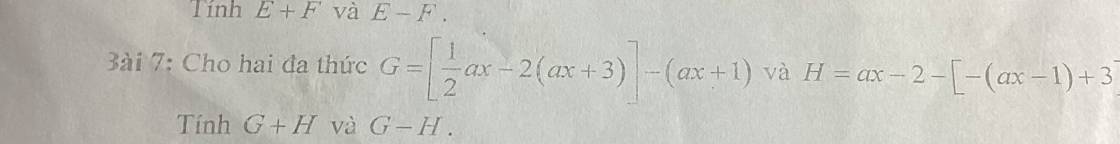
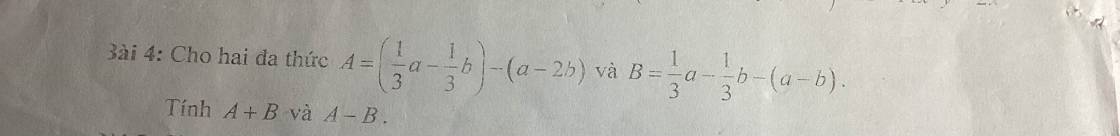
Gọi 3 số tự nhiên liên tiếp là \(a-1;a;a+1\)
Theo bài ra, ta có: \(a\times\left(a+1\right)-a\times\left(a-1\right)=12\)
\(a\times\left(a+1-a+1\right)=12\)
\(a\times2=12\)
\(a=12\div2\)
\(a=6\)
Vậy 3 số tự nhiên liên tiếp là \(5;6;7\)
Gọi \(n;n+1;n+2\left(n\in N\right)\) là 3 số tự nhiên liên tiếp
Theo đề bài ta có :
\(\left(n+1\right)\left(n+2\right)-n\left(n+1\right)=12\)
\(\Rightarrow n^2+3n+2-n^2-n=12\)
\(\Rightarrow2n+2=12\Rightarrow2\left(n+1\right)=12\Rightarrow n+1=6\Rightarrow n=5\)
Vậy 3 số đó là \(5;6;7\)