Cho x - y = -3 hãy tính giá trị của biểu thức P=x^3 + 3x^2 + y^2 - x²y - xy + x - 4y + 2023 (đề thi học sinh giỏi 7 huyện Nam đàn , tỉnh nghệ An 2022 - 2023 )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: \(2^x+2^{x+1}+...+2^{x+100}=2^{101}-1\)
=>\(2^x\left(1+2+...+2^{100}\right)=2^{101}-1\)
Đặt \(A=1+2+...+2^{100}\)
=>\(2A=2+2^2+...+2^{101}\)
=>\(2A-A=2+2^2+...+2^{101}-1-2-...-2^{100}\)
=>\(A=2^{101}-1\)
\(2^x\left(1+2+...+2^{100}\right)=2^{101}-1\)
=>\(2^x\left(2^{101}-1\right)=2^{101}-1\)
=>\(2^x=1=2^0\)
=>x=0
b: p là số nguyên tố lớn hơn 3 nên \(\left\{{}\begin{matrix}p⋮̸2\\p⋮̸3\end{matrix}\right.\)
p không chia hết cho 3 nên p=3k+1 hoặc p=3k+2
TH3: p=3k+1
\(\left(p-1\right)\left(p+1\right)\)
\(=\left(3k+1-1\right)\left(3k+1+1\right)\)
\(=3k\left(3k+2\right)⋮3\)(3)
TH2: p=3k+2
\(\left(p-1\right)\left(p+1\right)=\left(3k+2-1\right)\left(3k+2+1\right)\)
\(=\left(3k+1\right)\left(3k+3\right)=3\left(k+1\right)\left(3k+1\right)⋮3\)(2)
Từ (2),(3) suy ra \(\left(p-1\right)\left(p+1\right)⋮3\)
p không chia hết cho 2 nên p=2k+1
\(\left(p-1\right)\left(p+1\right)=\left(2k+1-1\right)\left(2k+1+1\right)\)
\(=2k\left(2k+2\right)=4k\left(k+1\right)\)
Vì k;k+1 là hai số nguyên liên tiếp
nên \(k\left(k+1\right)⋮2\)
=>\(4k\left(k+1\right)⋮4\cdot2\)
=>\(4k\left(k+1\right)⋮8\)
=>\(\left(p-1\right)\left(p+1\right)⋮8\)
mà \(\left(p-1\right)\left(p+1\right)⋮3\)
và ƯCLN(3;8)=1
nên \(\left(p-1\right)\left(p+1\right)⋮3\cdot8=24\)

a: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
\(\widehat{KBC}=\widehat{HCB}\)
Do đó: ΔKBC=ΔHCB
=>\(\widehat{KCB}=\widehat{HBC}\)
b: ΔKBC=ΔHCB
=>KC=HB

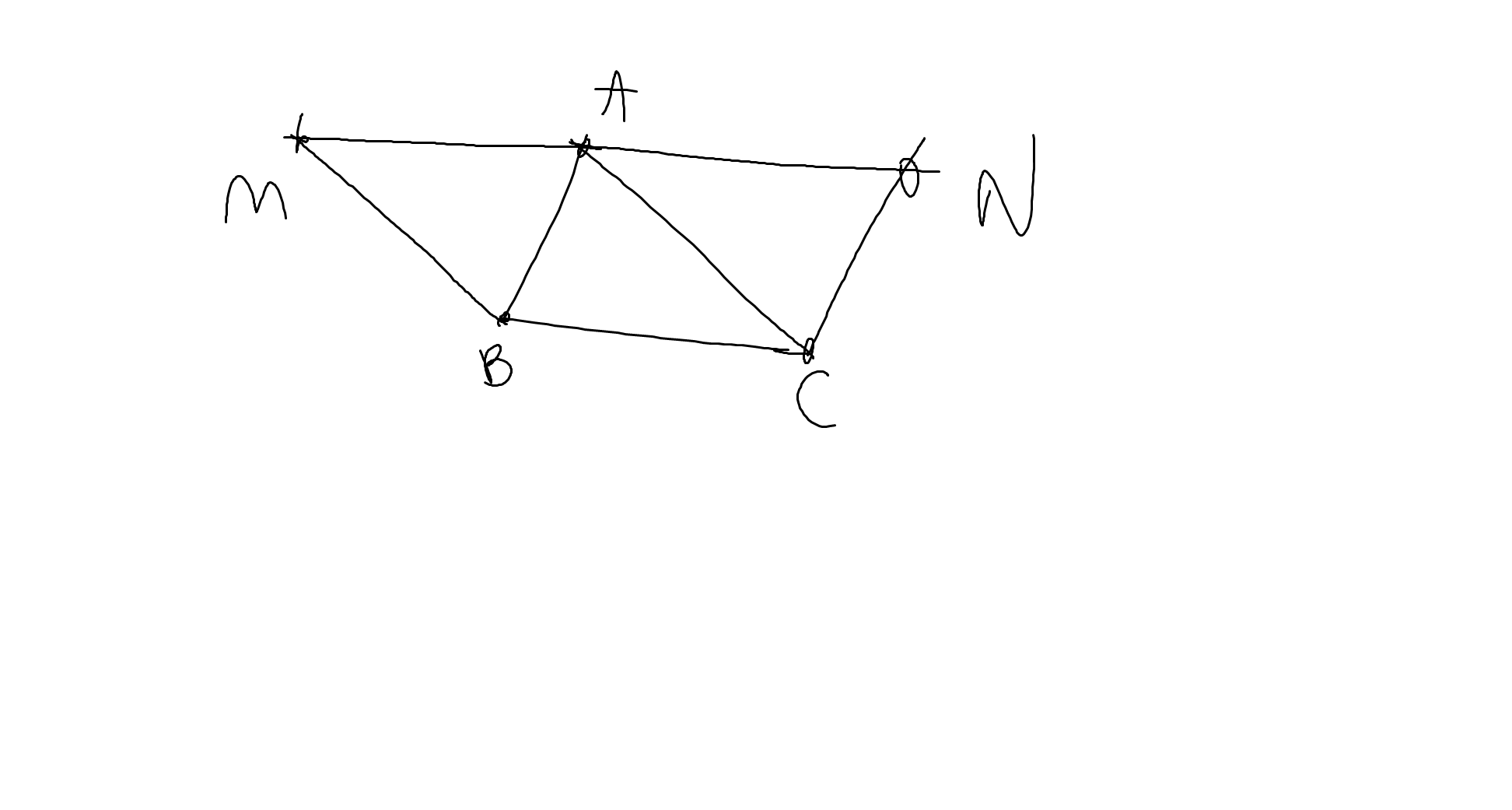
a: Xét ΔMAB và ΔCBA có
\(\widehat{MAB}=\widehat{ABC}\)(hai góc so le trong, MA//BC)
AB chung
\(\widehat{ABM}=\widehat{BAC}\)(hai góc so le trong, MB//AC)
Do đó;ΔMAB=ΔCBA
Xét ΔABC và ΔCNA có
\(\widehat{BAC}=\widehat{NCA}\)(hai góc so le trong, BA//CN)
AC chung
\(\widehat{BCA}=\widehat{NAC}\)(hai góc so le trong, AN//BC)
Do đó: ΔABC=ΔCNA
b: ΔMAB=ΔCBA
=>MA=CB
ΔABC=ΔCNA
=>BC=NA
mà BC=AM
nên AM=AN
mà M,A,N thẳng hàng
nên A là trung điểm của MN

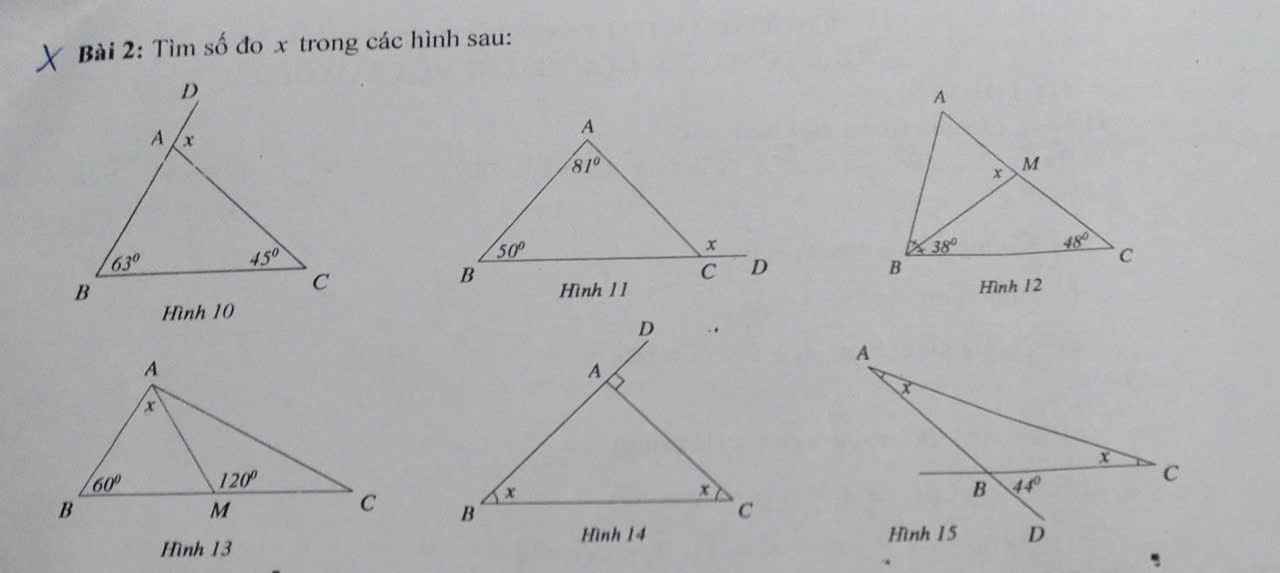
Hình 10: Xét ΔBAC có \(\widehat{CAD}\) là góc ngoài tại đỉnh A
nên \(\widehat{CAD}=\widehat{ABC}+\widehat{ACB}\)
=>\(x=63^0+45^0=108^0\)
Hình 11: Xét ΔABC có \(\widehat{ACD}\) là góc ngoài tại đỉnh C
nên \(\widehat{ACD}=\widehat{CAB}+\widehat{CBA}\)
=>\(x=81^0+50^0=131^0\)
Hình 12: Xét ΔBMC có \(\widehat{AMB}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMB}=\widehat{MBC}+\widehat{MCB}\)
=>\(x=38^0+48^0=86^0\)
Hình 13: Xét ΔMAB có \(\widehat{AMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMC}=\widehat{MAB}+\widehat{MBA}\)
=>\(x+60^0=120^0\)
=>\(x=60^0\)
Hình 14: Xét ΔBAC có \(\widehat{CAD}\) là góc ngoài tại đỉnh A
nên \(\widehat{CAD}=\widehat{ABC}+\widehat{ACB}\)
=>\(x+x=90^0\)
=>\(2x=90^0\)
=>\(x=45^0\)
Hình 15:
Xét ΔABC có \(\widehat{CBD}\) là góc ngoài tại đỉnh B
nên \(\widehat{CBD}=\widehat{BAC}+\widehat{BCA}\)
=>\(x+x=44^0\)
=>\(2x=44^0\)
=>\(x=22^0\)

Sau 1 năm, số tiền bác Dũng có:
75000000 + 75000000 . 5,6% = 79200000 (đồng)
Số tiền bác Dũng rút ra:
79200000 : 4 = 19800000 (đồng)
Số tiền bác Dũng còn lại trong ngân hàng:
79200000 - 19800000 = 59400000 (đồng)

\(\dfrac{1}{99}\) - \(\dfrac{1}{99.97}\) - \(\dfrac{1}{97.95}\) - .. - \(\dfrac{1}{3.1}\)
= \(\dfrac{1}{99}\) - (\(\dfrac{1}{99.97}+\dfrac{1}{95.93}+\dfrac{1}{3.1}\))
= \(\dfrac{1}{99}\) - \(\dfrac{1}{2}\) (\(\dfrac{2}{1.3}+\dfrac{2}{3.5}+..+\dfrac{2}{99.97}\))
= \(\dfrac{1}{99}\) - \(\dfrac{1}{2}\)(\(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\))
= \(\dfrac{1}{99}\) - \(\dfrac{1}{2}.\) (\(\dfrac{1}{1}\) - \(\dfrac{1}{99}\))
= \(\dfrac{1}{99}\) - \(\dfrac{1}{2}.\)\(\)\(\dfrac{98}{99}\)
= \(\dfrac{1}{99}\) - \(\dfrac{49}{99}\)
= - \(\dfrac{16}{33}\)

\(\dfrac{9^5-27^3+81^2}{\left(-63\right)}\)
Ta có: \(9=3^2\Rightarrow9^5=\left(3^2\right)^5=3^{10}\)
\(27=3^3\Rightarrow27^3=\left(3^3\right)^3=3^9\)
\(81=3^4\Rightarrow81^2=\left(3^4\right)^2=3^8\)
\(=\dfrac{3^{10}-3^9+3^8}{\left(-63\right)}\)
\(=\dfrac{3^9}{\left(-63\right)}\)
\(=\dfrac{45927}{\left(-63\right)}\)
\(=-729\)
\(\dfrac{9^5-27^3+81^2}{-63}\)
\(=\dfrac{3^{10}-3^9+3^8}{-63}=\dfrac{3^8\left(3^2-3+1\right)}{-63}\)
\(=\dfrac{-3^8\cdot\left(9-3+1\right)}{63}=\dfrac{-3^8}{3^2\cdot7}\cdot7=-3^6\)
=-729


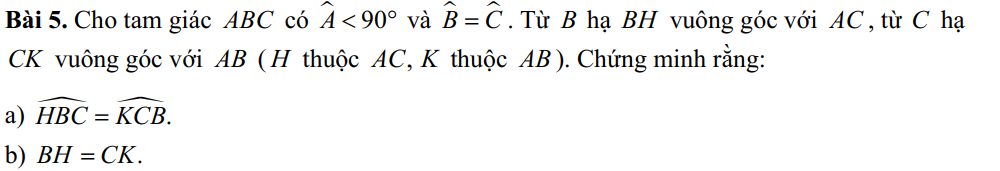

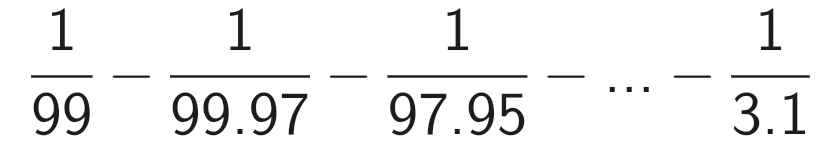
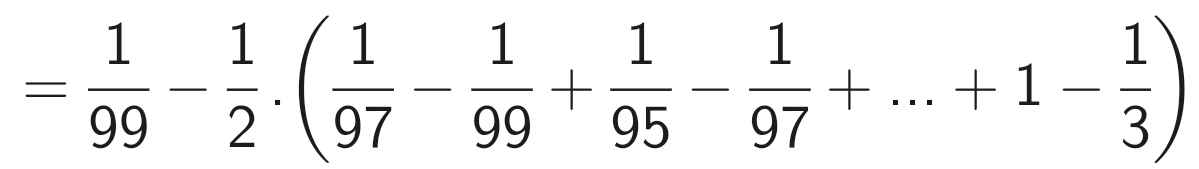
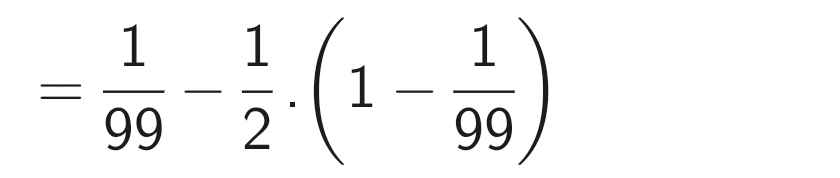
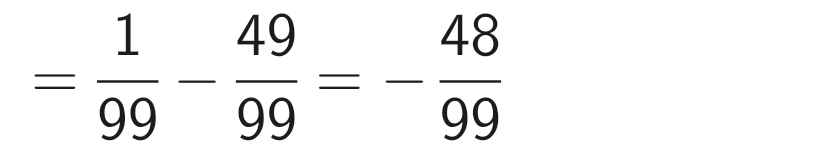
\(x-y=-3\Leftrightarrow x+3=y\)
\(P=x^2\left(x+3\right)+y^2-x^2y-xy+x-4y+2003=\)
\(=x^2y+y^2-x^2y-xy+x-4y+2023=\)
\(=y^2-xy-3y+x-y+2023=\)
\(=y^2-y\left(x+3\right)+x-y+2003=\)
\(=y^2-y^2+\left(x-y\right)+2023=-3+2023=2000\)