
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\widehat{C}=\widehat{B}+10^0=\widehat{A}+10^0+10^0=\widehat{A}+20^0\)
\(\widehat{D}=\widehat{C}+10^0=\widehat{A}+20^0+10^0=\widehat{A}+30^0\)
Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{A}+\widehat{A}+10^0+\widehat{A}+20^0+\widehat{A}+30^0=360^0\)
=>\(4\cdot\widehat{A}=300^0\)
=>\(\widehat{A}=75^0\)
\(\widehat{B}=75^0+10^0=85^0\)
\(\widehat{C}=75^0+20^0=95^0\)
\(\widehat{D}=75^0+30^0=105^0\)

a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{C}+\widehat{D}=360^0-110^0-70^0=180^0\)
=>\(\dfrac{1}{3}\cdot\widehat{D}+\widehat{D}=180^0\)
=>\(\dfrac{4}{3}\cdot\widehat{D}=180^0\)
=>\(\widehat{D}=135^0\)
\(\widehat{C}=\dfrac{1}{3}\cdot135^0=45^0\)
b:
Sửa đề: Cho tứ giác ABCD.
Đặt \(\widehat{B}=x;\widehat{C}=y;\widehat{D}=z\)
\(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}\)
=>\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)
Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(x+y+z=360^0-90^0=270^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{270}{9}=30^0\)
=>\(x=2\cdot30^0=60^0;y=3\cdot30^0=90^0;z=4\cdot30^0=120^0\)
Vậy: \(\widehat{B}=x=60^0;\widehat{C}=y=90^0;\widehat{D}=z=120^0\)

\(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}\)

\(\left(-5\right)^5=\left(-5\right)^4\cdot\left(-5\right)=5^4\cdot\left(-5\right)=625\cdot\left(-5\right)=-3125\)


\(\left(x^2-1\right)\left(x^2+2\right)< 0\)
mà \(x^2+2>0\forall x\)
nên \(x^2-1< 0\)
=>\(x^2< 1\)
=>-1<x<1

a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
b: AE=3CE
mà AE+CE=AC
nên \(CE=\dfrac{1}{4}AC\)
=>\(\dfrac{S_{CBE}}{S_{CAB}}=\dfrac{CE}{CA}=\dfrac{1}{4}=25\%\)

Nửa chu vi mảnh đất là 100:2=50(m)
Chiều rộng mảnh đất sau khi tăng thêm 32m là 50:2=25(m)
Chiều rộng ban đầu của mảnh đất là 25-32=-7<0
=>Đề sai rồi bạn
Giải:
Vì tăng chiều rộng thêm 32m, giảm chiều dài đi 32 thì được hình vuông nên chu vi của hình vuông bằng chu vi hình chữ nhật và bằng 100 cm
Cạnh hình vuông là: 100 : 4 = 25 (m)
25 < 32
Vậy không có hình chữ nhật nào thỏa mãn đề bài.
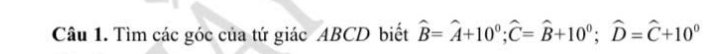
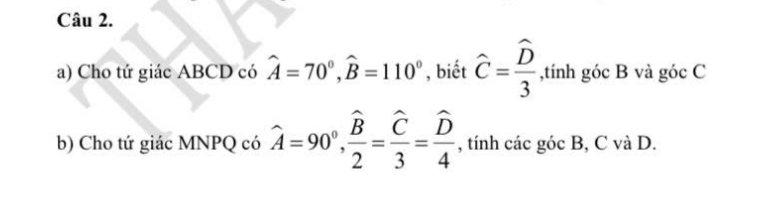
Bài 2:
a: \(27^{11}=\left(3^3\right)^{11}=3^{33};81^8=\left(3^4\right)^8=3^{32}\)
mà 33>32
nên \(27^{11}>81^8\)
b: \(625^5=\left(5^4\right)^5=5^{20};125^7=\left(5^3\right)^7=5^{21}\)
mà 20<21
nên \(625^5< 125^7\)
c: \(3^{2n}=\left(3^2\right)^n=9^n;2^{3n}=\left(2^3\right)^n=8^n\)
mà 9>8
nên \(3^{2n}>2^{3n}\)
Bài 3:
a: \(3^{1234}=\left(3^2\right)^{617}=9^{617};2^{1851}=\left(2^3\right)^{617}=8^{617}\)
mà 9>8
nên \(3^{1234}>2^{1851}\)
b: \(6^{30}=\left(6^2\right)^{15}=36^{15}>12^{15}\)
c: \(5^{36}=\left(5^3\right)^{12}=125^{12};11^{24}=\left(11^2\right)^{12}=121^{12}\)
mà 125>121
nên \(5^{36}>11^{24}\)
d: \(6^3=6\cdot6^2< 7\cdot6^2\)