có hai loại khay xếp Bánh loại 1 xếp được 6 cái loại hai xếp được ba cái các đĩa đều xếp đầy đủ Nam đếm được tất cả 129 cái vậy Nam đếm đúng hay sai Vì sao
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi:\(\dfrac{39}{6}=\dfrac{13}{2}\)
Chiều rộng mảnh đất là:
\(\dfrac{13}{2}\times\dfrac{1}{3}=\dfrac{13}{6}\left(cm\right)\)
Chu vi mảnh đất là:
\(2\times\left(\dfrac{13}{6}+\dfrac{13}{2}\right)=\dfrac{52}{3}\left(m\right)\)
Diện tích mảnh đất là:
\(\dfrac{13}{6}\times\dfrac{13}{2}=\dfrac{169}{12}\left(m^2\right)\)
Đ/S:...

\(S=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{200}}\)
\(\Rightarrow2S=2\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{200}}\right)\)
\(\Rightarrow2S=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{199}}\)
\(\Rightarrow2S-S=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{199}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{200}}\right)\)
\(\Rightarrow S=1-\dfrac{1}{2^{100}}< 1\)
\(\Rightarrow S< 1\)
Vậy \(S< 1\)

\(1.2\left(x+2\right)^2< 2x\left(x+2\right)+4\\ \Leftrightarrow2\left(x^2+4x+4\right)-2x\left(x+2\right)-4< 0\\ \Leftrightarrow2x^2+8x+4-2x^2-4x-4< 0\\ \Leftrightarrow4x< 0\\ \Leftrightarrow x< 0\\ 2.\left(x-1\right)^2+x^2< \left(x+1\right)^2+\left(x+2\right)^2\\ \Leftrightarrow x^2-2x+1+x^2< x^2+2x+1+x^2+4x+4\\ \Leftrightarrow2x^2-2x+1-2x^2-6x-5< 0\\ \Leftrightarrow-8x-4< 0\\ \Leftrightarrow8x>-4\\ \Leftrightarrow x>-\dfrac{1}{2}\\ 3.\left(x^2+1\right)\left(x-6\right)< \left(x-2\right)^3\\ \Leftrightarrow x^3-6x^2+x-6< x^3-6x^2+12x-8\\ \Leftrightarrow x-6< 12x-8\\ \Leftrightarrow12x-x>-6+8\\ \Leftrightarrow11x>2\\ \Leftrightarrow x>\dfrac{2}{11}\)

a: Xét ΔBAD và ΔABC có
AB chung
BD=AC
AD=BC
Do đó: ΔBAD=ΔABC
=>\(\widehat{ABD}=\widehat{BAC}\)
=>\(\widehat{TAB}=\widehat{TBA}\)
=>ΔTAB cân tại T
=>TA=TB
b: Ta có: TA+TC=AC
TB+TD=BD
mà TA=TB và AC=BD
nên TC=TD
nối t với m sao cho tm vuông góc ab
xét tam giác AMT và tam giác BMT có
amt=bmt=90 độ
mt chung
am=mb
suy ra hai tam giác bằng nhau
suy ra ta=tb
CMTT ta có tam giác TDN và TCN
suy ra TD=TC

Bài 18:
a: \(\left(-\dfrac{40}{51}\cdot0,32\cdot\dfrac{17}{20}\right):\dfrac{64}{75}\)
\(=-\dfrac{40}{20}\cdot\dfrac{17}{51}\cdot\dfrac{8}{25}\cdot\dfrac{75}{64}\)
\(=-\dfrac{2}{3}\cdot\dfrac{8}{64}\cdot\dfrac{75}{25}=-\dfrac{2}{3}\cdot3\cdot\dfrac{1}{8}=-\dfrac{2}{8}=-\dfrac{1}{4}\)
b: \(-\dfrac{10}{11}\cdot\dfrac{8}{9}+\dfrac{7}{18}\cdot\dfrac{10}{11}=\dfrac{10}{11}\left(-\dfrac{8}{9}+\dfrac{7}{18}\right)\)
\(=\dfrac{10}{11}\left(-\dfrac{16}{18}+\dfrac{7}{18}\right)=\dfrac{10}{11}\cdot\dfrac{-9}{18}=\dfrac{10}{11}\cdot\dfrac{-1}{2}=-\dfrac{5}{11}\)
c: \(\dfrac{3}{14}:\dfrac{1}{28}-\dfrac{13}{21}:\dfrac{1}{28}+\dfrac{29}{42}:\dfrac{1}{28}-8\)
\(=\left(\dfrac{3}{14}-\dfrac{13}{21}+\dfrac{29}{42}\right):\dfrac{1}{28}-8\)
\(=\left(\dfrac{9}{42}-\dfrac{6}{42}+\dfrac{29}{42}\right):\dfrac{1}{28}-8\)
\(=\dfrac{32}{42}\cdot28-8=32\cdot\dfrac{2}{3}-8=\dfrac{64}{3}-\dfrac{24}{3}=\dfrac{40}{3}\)
d: \(-1\dfrac{5}{7}\cdot15+\dfrac{2}{7}\cdot\left(-15\right)+\left(-105\right)\left(\dfrac{2}{3}-\dfrac{4}{5}+\dfrac{1}{7}\right)\)
\(=-\dfrac{12}{7}\cdot15+\dfrac{2}{7}\cdot\left(-15\right)+\left(-105\right)\left(\dfrac{70}{105}-\dfrac{84}{105}+\dfrac{15}{105}\right)\)
\(=\dfrac{-180-30}{7}+\left(-105\right)\cdot\dfrac{1}{105}\)
=-30-1=-31
Bài 19:
a: \(A=7x-2x-\dfrac{2}{3}y+\dfrac{7}{9}y=5x+y\left(\dfrac{7}{9}-\dfrac{2}{3}\right)=5x+\dfrac{y}{9}\)
Khi x=-1/10;y=4,8 thì \(A=5\cdot\dfrac{-1}{10}+\dfrac{4.8}{9}\)
\(=-\dfrac{1}{2}+\dfrac{8}{15}=\dfrac{-15+16}{30}=\dfrac{1}{30}\)
b: \(B=x+\dfrac{0,2-0,375+\dfrac{5}{11}}{-0,3+\dfrac{9}{16}-\dfrac{15}{22}}\)
\(=x+\dfrac{\dfrac{2}{10}-\dfrac{6}{16}+\dfrac{10}{22}}{-\dfrac{3}{10}+\dfrac{9}{16}-\dfrac{15}{22}}=x+\dfrac{2\left(\dfrac{1}{10}-\dfrac{3}{16}+\dfrac{5}{22}\right)}{-3\left(\dfrac{1}{10}-\dfrac{3}{16}+\dfrac{5}{22}\right)}\)
\(=x-\dfrac{2}{3}\)
Khi x=-1/3 thì \(B=-\dfrac{1}{3}-\dfrac{2}{3}=-\dfrac{3}{3}=-1\)

Giá tiền mỗi buổi học trực tuyến là \(150000\times\dfrac{8}{15}=80000\left(đồng\right)\)
Số buổi học trong 1 năm là 4x12=48(buổi)
Số tiền tiết kiệm được là:
\(48\times\left(150000-80000\right)=48\times70000=3360000\left(đồng\right)\)

Hướng giải:
- Chứng minh được đường phân giác trong và đường phân giác ngoài của cùng 1 góc thì vuông góc với nhau
- Từ đó chững minh được APBQ và AMCN là hình chữ nhật.
- Gọi I là giao của PQ với AB; K là giao của MN với AC => I là trung điểm của AB và K là trung điểm của AC (trong HCN 2 đường chéo cắt nhau tại trung điểm mỗi đường)
- Ta chứng minh được \(\widehat{QNy}=\widehat{BCy}\) Hai góc này ở vị trí đồng vị
=> MN//BC
- Chứng minh tương tự ta cũng có PQ//BC
- Xét tg ABC có PQ đi qua trung điểm AB và PQ//BC => PQ đi qua trung điểm K của AC (Trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
=> Qua điểm K có 2 đường thẳng PQ và MN cùng song song với BC nên MN trùng PQ hay P; Q; M; N thẳng hàng (Từ 1 điểm bên ngoài 1 đường thẳng cho trước chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)

Giá tiền mỗi buổi học trực tuyến là \(150000\times\dfrac{8}{15}=80000\left(đồng\right)\)
Số buổi học trong 1 năm là 4x12=48(buổi)
Số tiền tiết kiệm được là:
\(48\times\left(150000-80000\right)=48\times70000=3360000\left(đồng\right)\)
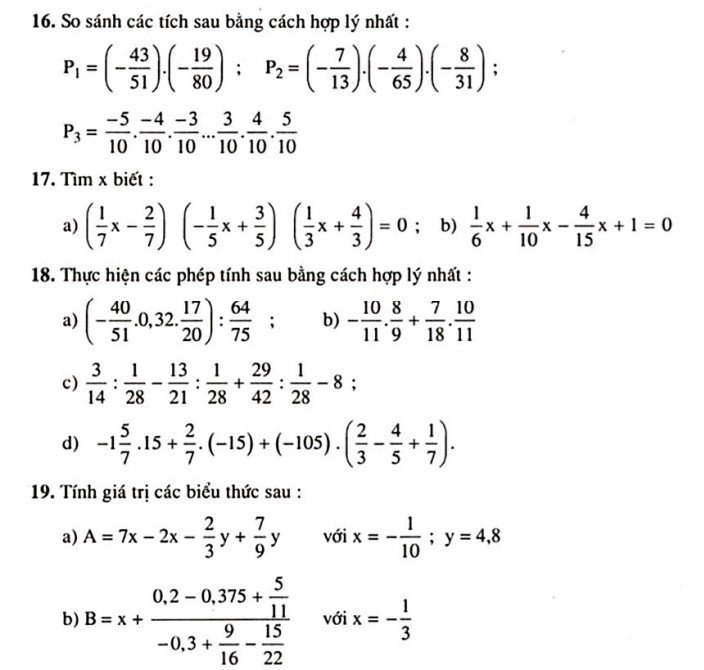
Nam đếm được 129 cái gì.