Bài 3. (1 điểm) Tam giác $ABC$ có $AB = 21$, $AC = 16$ và $\widehat{BAC} = 60^\circ$. Tính bán kính đường tròn nội tiếp $r$ của tam giác $ABC$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


30 tháng 10 2023
Xét tam giác ABC có ta có:
(định lí tổng ba góc trong tam giác)
Áp dụng định lí sin trong tam giác ABC, ta có:
TC
46

DT
Dang Tung
CTVHS
20 tháng 10 2023
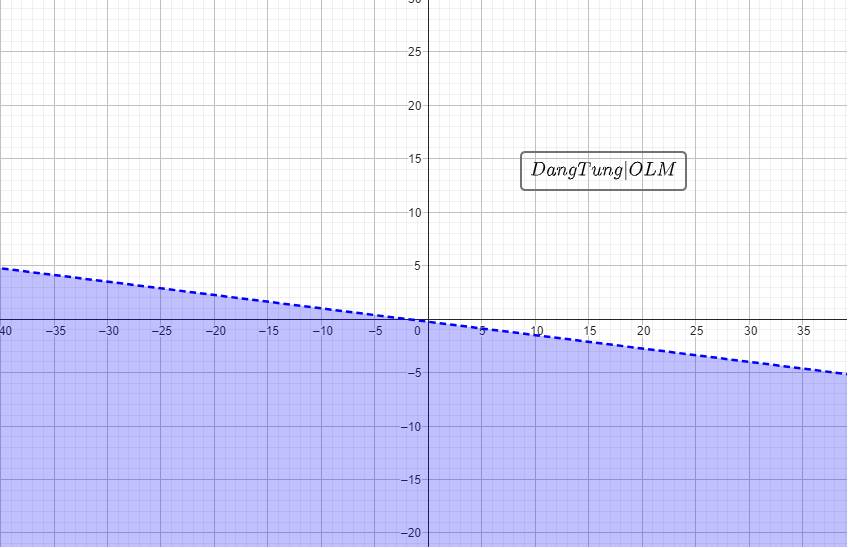
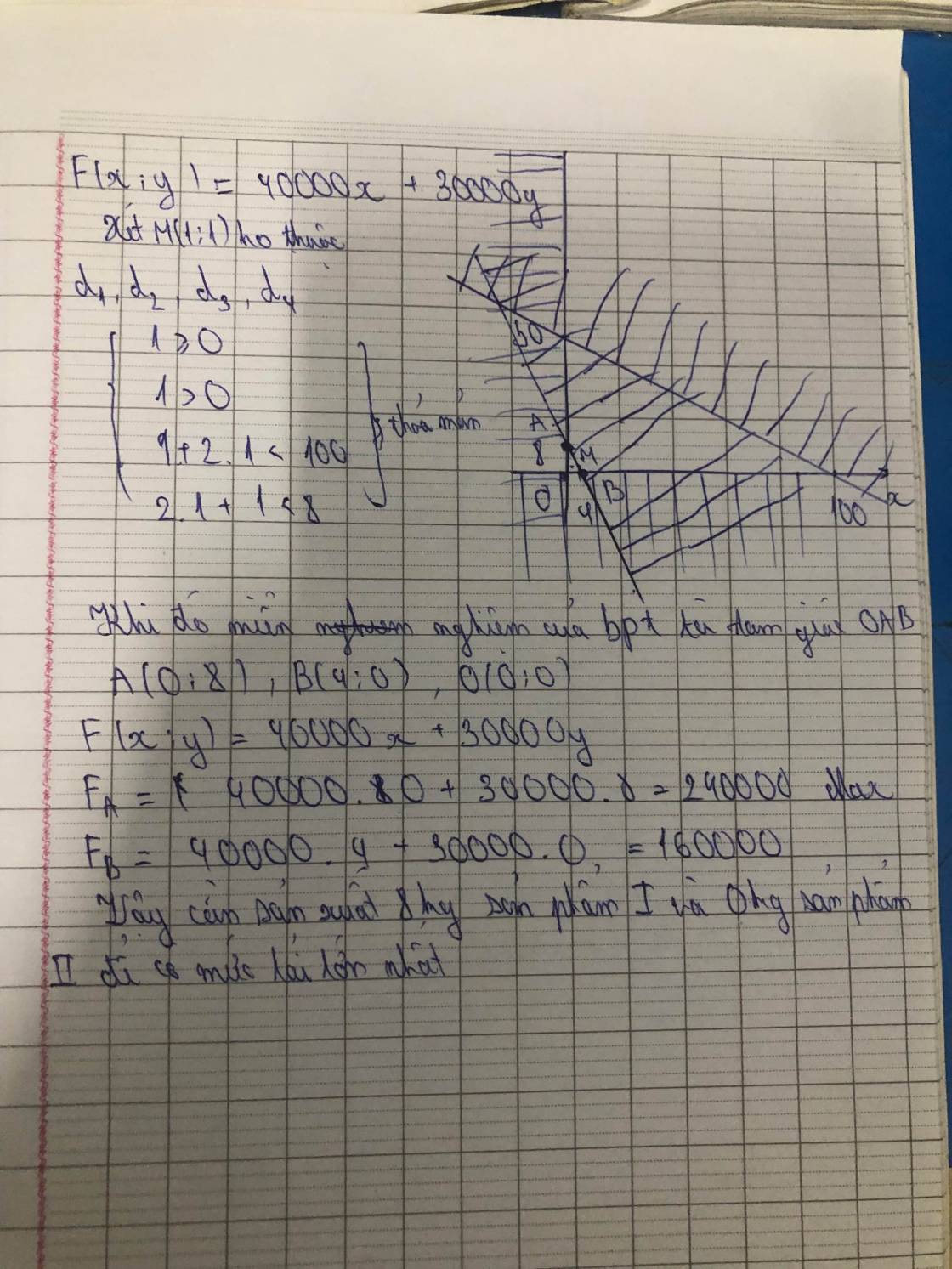
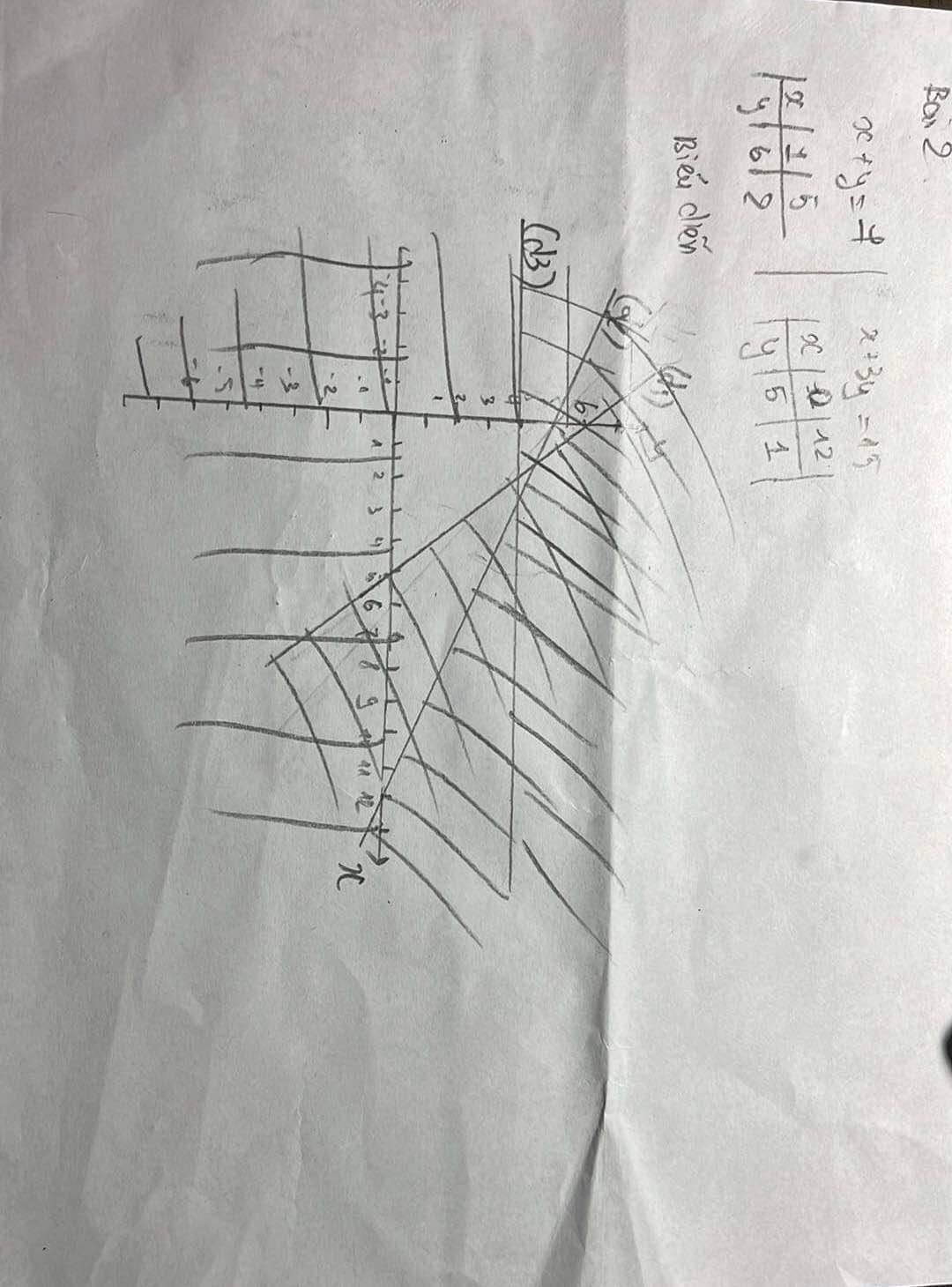
\(\dfrac{x-2y}{2}>\dfrac{2x+y+1}{3}\\ < =>3\left(x-2y\right)>2\left(2x+y+1\right)\\ < =>3x-6y>4x+2y+2\\ < =>4x-3x+2y+6y< -2\\ < =>x+8y< -2\)

DT
Dang Tung
CTVHS
20 tháng 10 2023
a) \(A\cap B=\left\{2;3;4\right\}\\ A\cup B=\left\{0;1;2;3;4;5;6\right\}\)
b) Để hàm số xđ thì : \(2-x\ge0< =>-x\ge-2< =>x\le2\)
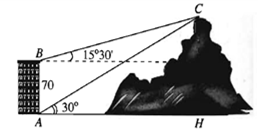

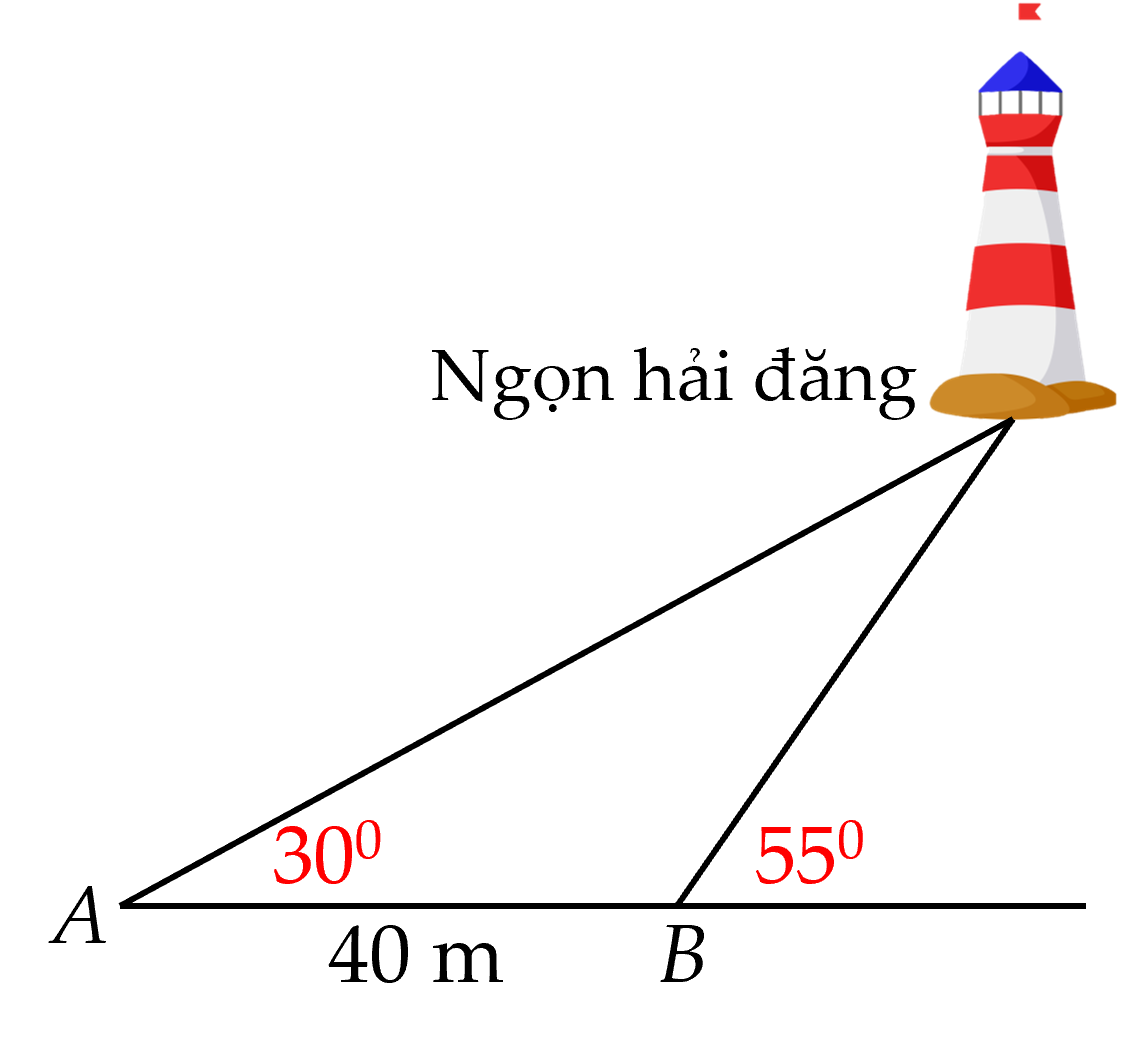


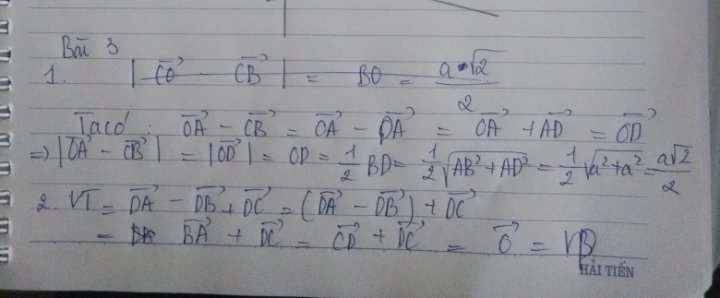




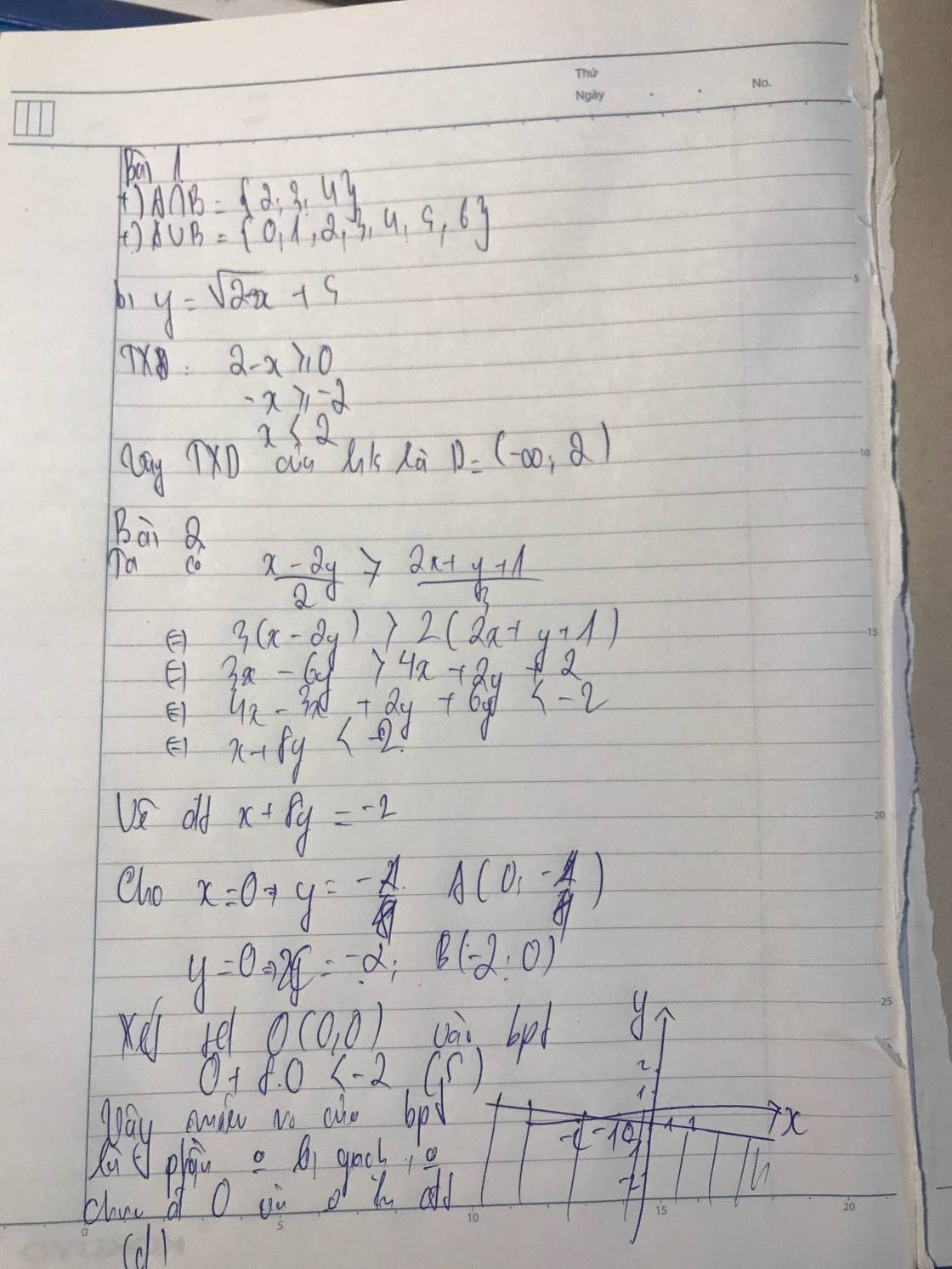
Áp dụng định lý cosin cho tam giác ABC, ta được:
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}\)
\(=\sqrt{21^2+16^2-2.21.16.cos60^o}\)
\(=19\)
Do đó \(p=\dfrac{AB+BC+CA}{2}=\dfrac{21+16+19}{2}=28\)
Mà \(S_{ABC}=\dfrac{1}{2}AB.AC.sinA=\dfrac{1}{2}.21.16.sin60^o=84\sqrt{3}\)
Mặt khác, \(S_{ABC}=pr=28r\) (\(r\) là bán kính đường tròn nội tiếp \(\Delta ABC\))
\(\Rightarrow28r=84\sqrt{3}\Leftrightarrow r=3\sqrt{3}\)