b) 5( 2x + 3 )( x + 2 ) - 2( 5x - 4 )( x - 1 ) = 75

<=> 5( 2x² + 7x + 6 ) - 2( 5x² - 9x + 4 ) = 75

<=> 10x² + 35x + 30 - 10x² + 18x - 8 = 75

<=> 53x + 22 = 75

<=> 53x = 53

<=> x = 1

c) 2x² + 3( x - 1 )( x + 1 ) = 5x( x + 1 )

<=> 2x² + 3( x² - 1 ) = 5x² + 5x

<=> 2x² + 3x² - 3 - 5x² - 5x = 0

<=> -3 - 5x = 0

<=> -5x = 3

<=> x = -3/5

b, \(5\left(2x+3\right)\left(x+2\right)-2\left(5x-4\right)\left(x-1\right)=75\)

\(\Leftrightarrow10x^2+20x+15x+30-10x^2+10x+8x-8=75\)

\(\Leftrightarrow53x+22=75\Leftrightarrow x=1\)

A = x² + xy + y² + 1

A = (x² + xy + 1/4y²) + 3/4y² + 1

A = (x + 1/2y)² + 3/4y² + 1 \(\ge\)1 với mọi x;y

Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+\frac{1}{2}y=0\\\frac{3}{4}y=0\end{cases}}\) <=> \(\hept{\begin{cases}x=-\frac{1}{2}y\\y=0\end{cases}}\)<=> x = y = 0

Vậy MinA = 1 khi x = y = 0

Ta có :

\(A=x^2+xy+y^2+1\)

\(=\left(x^2+xy+y^2\right)+1\)

\(=\left(x^2+2\cdot x\cdot\frac{1}{2}+\frac{y^2}{4}\right)+\frac{3y^2}{4}+1\)

\(=\left(x+\frac{y}{2}\right)^2+\frac{3y^2}{4}+1\ge1\)

Dấu "=" xảy ra \(\Leftrightarrow x=y=0\)

Vậy \(A_{min}=1\) tại \(x=y=0\)

Mình chỉ làm đc có nhiêu đây thôi

bn k cho mình nhoa 

x³- 4x + 5 = x³ + x² -x² +4x -5

=x²(x+1) - (x² -4x +5)

ta có  x² -4x +5 = x² -5x +x-5 = x(x-5) + (x-5) = (x+1)(x-5)

thay vào pt ta dc   x²(x+1) - (x+1)(x-5)  = (x+1)(x² -x +5)  =0

với x+1 =0 thì x=1

x² -x +5 = x² - x +\(\frac{1}{4}\) +\(\frac{19}{4}\) = (x-\(\frac{1}{2}\))² +\(\frac{19}{4}\)>0.

vậy S=(1)

a) xét tam giác ABD và tam giác ACE, có:

AB = AC (gt)

^A chung

^B₁ = ^C₁ (= 1/2^B = 1/2^C)

nên tam giác ABD = tam giác ACE (g.c.g)

=> AD = AE 

vì BEDC là hình thang cân nên DE // BC

=> ^D₁ = ^B₂ (sole trong)

lại có ^B₂ = ^B₁ nên ^B₁ = ^D₁

=> EBD cân

=> EB = ED

vậy BEDC là hình thang cân và có đáy nhỏ bằng cạnh bên

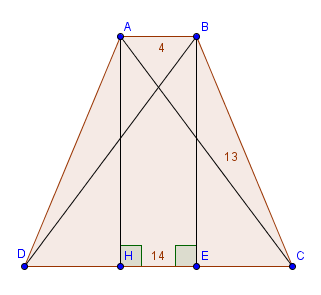
Kẻ đường cao AH, BE

Ta có : AB // CD
Mà AH $\perp$ CD
BE $\perp$ CD
$\implies$ AH, BE $\perp$ AB, CD
$\implies$ ABEH là hình chữ nhật

Xét $\triangle$ ADH vuông tại H và $\triangle$ BCE vuông tại E có :
AD = BC
$\hat{D} = \hat{C}$
Vậy $\triangle$ ADH = $\triangle$ BCE (ch-gn)

Lại có : $DH+CE = CD - HE = CD - AB = 14 - 4 = 10$
Mà $DH = CE$ ( $\triangle$ ADH = $\triangle$ BCE )
$\implies DH = CE = \dfrac{10}2 = 5$

Xét $\triangle$ BEC vuông tại E có :
$BE^2 = BC^2-CE^2=13^2-5^2=169-25=144 \\
\implies BE = 12$

Xét $\triangle$ BDE vuông tại E có :
$BD^2=BE^2+DE^2=BE^2+(DH+HE)^2=BE^2+(DH+AB)^2=12^2 +(5+4)^2=12^2+9^2=144+81=225$
$\implies$ BD = AC = 15

                                                                                            Giải

a, Kẻ BN \(\perp\)AD, BM\(\perp\)CD

Xét \(\Delta\)BNA và \(\Delta\)BMD, có : 

+ AB=AC

+ \(\widehat{\text{BNA}}\)=180* - \(\widehat{\text{BAD=}}\)70* nên \(\widehat{\text{BAN}}\)=\(\widehat{\text{BCD=}}\)70*

\(\Rightarrow\Delta\)BNA = \(\Delta\)BMD (ch-gn)

a﴿ Kẻ BN vuông AD, BM vuông CD

Xét tam giác vuông BNA và BMD có

: AB = BC ; góc BNA = 180 độ

‐ góc BAD = 70 độ

nên góc BAN = góc BCD = 70 độ

=> tam giác BMD = tam giác BND ﴾cạnh huyền ‐ góc nhọn﴿

=> BN = BM => BD là phân giác góc D

b﴿ Nối B vs D, do AB = AD nên tam giác ABD cân tại A

khi đó góc ADB = ﴾180 ‐110) :2= 35 độ

=> góc ADC = 70 Do góc ADC + góc BAD = 180 => AB // CD

Và góc BCD = góc ADC = 70 độ

=> ABCD là hình thang cân

a) Thiếu đề nha !!!!!!

b)

Đặt:    \(\left(x^2-x+1\right)^2=a;x^2=b\)

=> TA CÓ PT MỚI SAU:    \(a^2-10ab+9b^2=0\)

<=>   \(a^2-ab-9ab+9b^2=0\)

<=>   \(\left(a-b\right)\left(a-9b\right)=0\)

<=>   \(\orbr{\begin{cases}a=b\\a=9b\end{cases}}\)

TH1:    \(a=b\)     

=>    \(\left(x^2-x+1\right)^2=x^2\)     \(\)

<=>   \(\orbr{\begin{cases}x^2-x+1=x\\x^2-x+1=-x\end{cases}}\)

<=>   \(\orbr{\begin{cases}x^2-2x+1=0\\x^2+1=0\end{cases}}\)

<=>   \(\orbr{\begin{cases}\left(x-1\right)^2=0\\do:x^2\ge0\forall x\end{cases}}\)

=>    \(\orbr{\begin{cases}x=1\\x^2+1\ge1>0\end{cases}}\)

=>    pt:    \(x^2+1=0\)      vô nghiệm.

TH2:    \(a=9b\)

=>    \(\left(x^2-x+1\right)^2=9x^2\)

<=>   \(\orbr{\begin{cases}x^2-x+1=3x\\x^2-x+1=-3x\end{cases}}\)

<=>    \(\orbr{\begin{cases}x^2-4x+1=0\\x^2+2x+1=0\end{cases}}\)

<=>    \(\hept{\begin{cases}x=2+\sqrt{3}\\x=2-\sqrt{3}\\x=-1\end{cases}}\)

VẬY TẬP HỢP NGHIỆM CỦA PT LÀ: \(S=\left\{1;-1;2+\sqrt{3};2-\sqrt{3}\right\}\)

Câu a thiếu =0 nhé

a) Đặt x +y = S; xy = P => S; P nguyên 

Ta có: \(x^2+y^2=\left(xy-3\right)^2\Leftrightarrow\left(x+y\right)^2-2xy=\left(xy\right)^2-6xy+9\)

=> \(S^2-2P=P^2-6P+9\)

<=> \(S^2-\left(P-2\right)^2=5\)

<=> \(\left(S-P+2\right)\left(S+P-2\right)=5\)

TH1: \(\hept{\begin{cases}S-P+2=5\\S+P-2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}S-P=3\\S+P=3\end{cases}\Leftrightarrow\hept{\begin{cases}S=3\\P=0\end{cases}}}\)

khi đó: \(\hept{\begin{cases}x+y=3\\xy=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3;y=0\\x=0;y=3\end{cases}}\)

TH2: \(\hept{\begin{cases}S-P+2=1\\S+P-2=5\end{cases}}\Leftrightarrow\hept{\begin{cases}S-P=-1\\S+P=7\end{cases}\Leftrightarrow\hept{\begin{cases}S=3\\P=4\end{cases}}}\)

khi đó: \(\hept{\begin{cases}x+y=3\\xy=4\end{cases}}\)<=> không tồn tại x; y nguyên 

TH3: \(\hept{\begin{cases}S-P+2=-5\\S+P-2=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}S-P=-7\\S+P=1\end{cases}\Leftrightarrow\hept{\begin{cases}S=-3\\P=4\end{cases}}}\)

khi đó: \(\hept{\begin{cases}x+y=-3\\xy=4\end{cases}}\)<=> không tồn tại x; y nguyên 

TH4: \(\hept{\begin{cases}S-P+2=-1\\S+P-2=-5\end{cases}}\Leftrightarrow\hept{\begin{cases}S-P=-3\\S+P=-3\end{cases}\Leftrightarrow\hept{\begin{cases}S=-3\\P=0\end{cases}}}\)

Khi đó: \(\hept{\begin{cases}x+y=-3\\xy=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-3;y=0\\x=0;y=-3\end{cases}}\)

Vậy  có 4 nghiệm nguyên ( 3; 0) ( -3: 0) ( 0; 3) ( 0; -3)

Ta có : a² + b² = c²

=> a² + b² - c² = 0

=> a² + b² + 2ab - c² = 2ab

=> (a + b)² - c² = 2ab

=> (a + b - c)(a + b + c) = 2ab

=> (a + b - c)/2 . (a + b + c) = ab

=> ab \(⋮\)a + b + c (đpcm)

Bạn Xyz làm sai rồi nhé !!!!!

Chỗ:    \(\left(\frac{a+b-c}{2}\right)\left(a+b+c\right)=ab\)

Đoạn này để có:    \(ab⋮\left(a+b+c\right)\)     thì bạn phải lập luận     \(\frac{a+b-c}{2}\inℤ\)     đã nhé !!!!!! 

(NẾU BẠN SUY LUÔN RA     \(ab⋮\left(a+b+c\right)\)   LÀ SAI RỒI)

=> Cần phải chứng minh:     \(a+b-c⋮2\) 

Có: \(a^2+b^2=c^2\)

=> Nếu a chẵn; b chẵn thì c cũng chẵn        =>    \(a+b-c⋮2\) 

Nếu a chẵn; b lẻ thì c lẻ    =>   b - c chẵn     =>   \(a+b-c⋮2\)

Nếu a lẻ; b lẻ thì c chẵn    =>   a + b chẵn    =>   \(a+b-c⋮2\)

Nếu a lẻ; b chẵn thì c lẻ    =>   a - c chẵn     =>   \(a+b-c⋮2\)

VẬY QUA 4 TRƯỜNG HỢP THÌ TA =>   \(\frac{a+b-c}{2}\inℤ\)

Khi đó thì      \(ab⋮\left(a+b+c\right)\)

TA CÓ ĐPCM !!!!!