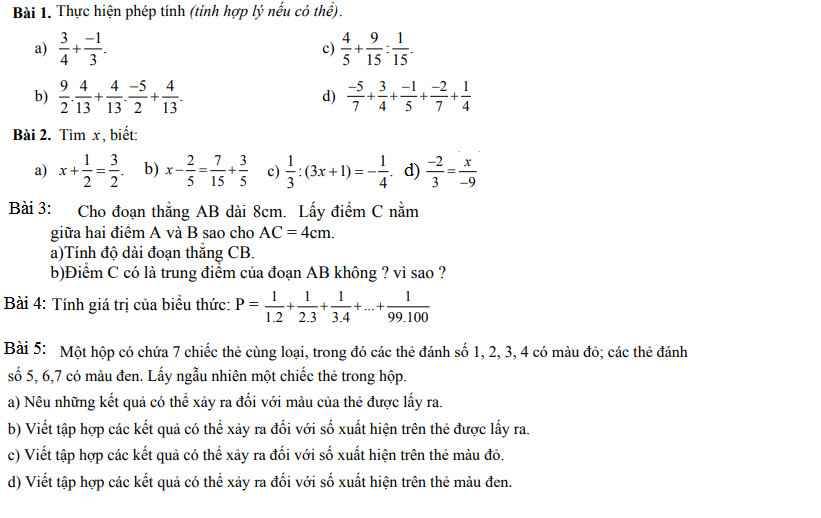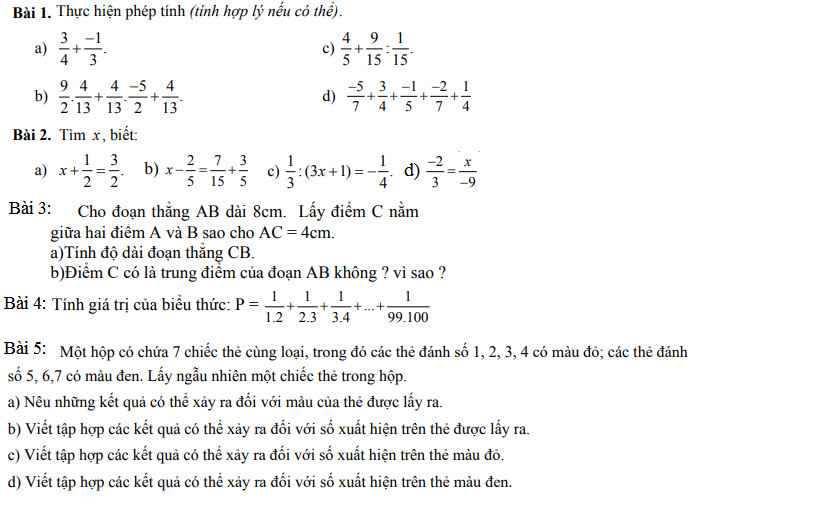Giải phương trình sau: 10/(x^2+4x+8)+9/(x^2+4x+6)-8/(x^2+4x+7)=1/2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


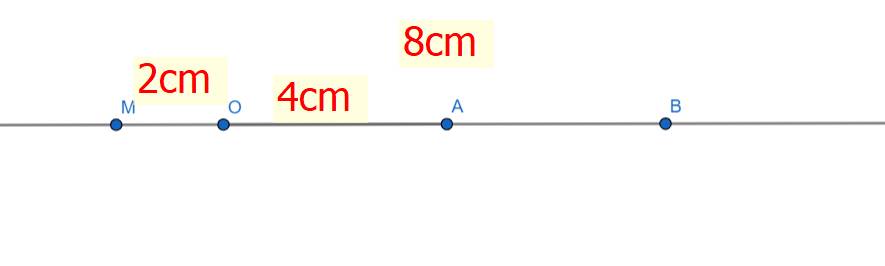
a) Ta có: \(OB>OA\)
⇒ A nằm giữa O và B
\(\Rightarrow OB=AB+OA\)
\(\Rightarrow AB=OB-OA\)
\(\Rightarrow AB=8-4=4\left(cm\right)\)
Mà: \(AB=OA=4\left(cm\right)\)
⇒ A là trung điểm của OB
b) O nằm giữa A và M
\(\Rightarrow OM+OA=MA\)
\(\Rightarrow MA=OM+OA=2+4=6\left(cm\right)\)
\(\Rightarrow AB< MA\) (vì 4 < 6)

Bài 1:
a) \(\dfrac{3}{4}+\dfrac{-1}{3}\)
\(=\dfrac{9}{12}+\dfrac{-4}{12}\)
\(=\dfrac{5}{12}\)
b) \(\dfrac{4}{5}+\dfrac{9}{15}:\dfrac{1}{15}\)
\(=\dfrac{4}{5}+\dfrac{9}{15}\cdot\dfrac{15}{1}\)
\(=\dfrac{4}{5}+\dfrac{9}{1}\)
\(=\dfrac{4}{5}+\dfrac{45}{5}\)
\(=\dfrac{49}{5}\)
c) \(\dfrac{9}{2}\cdot\dfrac{4}{13}+\dfrac{4}{13}\cdot\dfrac{-5}{2}+\dfrac{4}{13}\)
\(=\dfrac{4}{13}\cdot\left(\dfrac{9}{2}-\dfrac{5}{2}+1\right)\)
\(=\dfrac{4}{13}\cdot\left(\dfrac{4}{2}+1\right)\)
\(=\dfrac{4}{13}\cdot3\)
\(=\dfrac{12}{13}\)
d) \(\dfrac{-5}{7}+\dfrac{3}{4}+\dfrac{-1}{5}+\dfrac{-2}{7}+\dfrac{1}{4}\)
\(=\left[\left(\dfrac{-5}{7}+\dfrac{-2}{7}\right)+\left(\dfrac{3}{4}+\dfrac{1}{4}\right)\right]+\dfrac{-1}{5}\)
\(=\left(\dfrac{-7}{7}+\dfrac{4}{4}\right)+\dfrac{-1}{5}\)
\(=\left(-1+1\right)-\dfrac{1}{5}\)
\(=-\dfrac{1}{5}\)

Olm chào em, em cần đăng rõ ràng nội dung câu hỏi để nhận sự trợ giúp tốt nhất cho tài khoản olm vip em nhé.

Bài 4:
\(P=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3}\right)+...+\left(\dfrac{1}{99}-\dfrac{1}{99}\right)-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}\)
\(=\dfrac{100}{100}-\dfrac{1}{100}\)
\(=\dfrac{99}{100}\)

b; [\(\dfrac{5}{4}\) + \(\dfrac{3}{4}\)].\(\dfrac{4}{7}\) + [\(\dfrac{3}{4}\) + \(\dfrac{9}{4}\)].\(\dfrac{4}{7}\)
= 2.\(\dfrac{4}{7}\) + 3.\(\dfrac{4}{7}\)
= \(\dfrac{4}{7}\).(2+3)
= \(\dfrac{4}{7}\).5
= \(\dfrac{20}{7}\)
a; \(\dfrac{4}{9}\).[\(\dfrac{5}{7}\) + \(\dfrac{2}{5}\)] - \(\dfrac{4}{9}\).[- \(\dfrac{2}{7}\) + \(\dfrac{7}{5}\)]
= \(\dfrac{4}{9}.\dfrac{5}{7}\) + \(\dfrac{4}{9}.\dfrac{2}{5}\) + \(\dfrac{4}{9}\).\(\dfrac{2}{7}\) - \(\dfrac{4}{9}\).\(\dfrac{7}{5}\)
= (\(\dfrac{4}{9}\).\(\dfrac{5}{7}\) + \(\dfrac{4}{9}\).\(\dfrac{2}{7}\)) + (\(\dfrac{4}{9}\).\(\dfrac{2}{5}\) - \(\dfrac{4}{9}\).\(\dfrac{7}{5}\))
= \(\dfrac{4}{9}\).(\(\dfrac{5}{7}\) + \(\dfrac{2}{7}\)) + \(\dfrac{4}{9}\).(\(\dfrac{2}{5}\) - \(\dfrac{7}{5}\))
= \(\dfrac{4}{9}\) - \(\dfrac{4}{9}\)
= 0

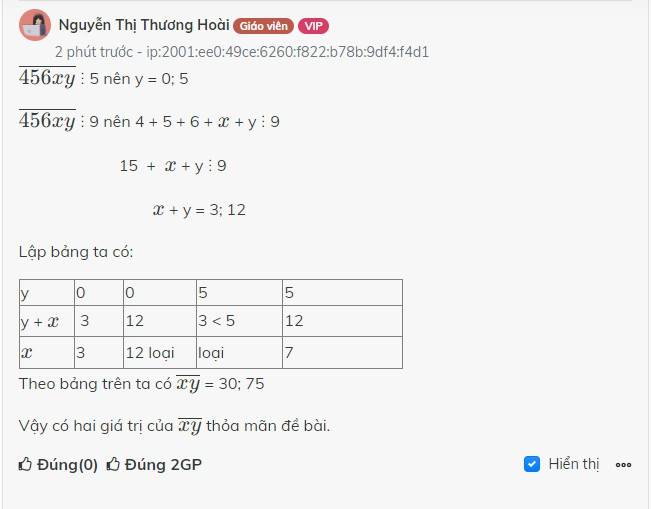
\(\overline{456xy}\) ⋮ 5 nên y = 0; 5
\(\overline{456xy}\) ⋮ 9 nên 4 + 5 + 6 + \(x\) + y ⋮ 9
15 + \(x\) + y ⋮ 9
\(x\) + y = 3; 12
Lập bảng ta có:
| y | 0 | 0 | 5 | 5 |
| y + \(x\) | 3 | 12 | 3 < 5 | 12 |
| \(x\) | 3 | 12 loại | loại | 7 |
Theo bảng trên ta có \(\overline{xy}\) = 30; 75
Vậy có hai giá trị của \(\overline{xy}\) thỏa mãn đề bài.