a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔBAD=ΔBED
=>DA=DE

b: DA=DE

=>D nằm trên đường trung trực của AE(1)

Ta có: BA=BE

=>B nằm trên đường trung trực của AE(2)

Từ (1),(2) suy ra BD là đường trung trực của AE

=>F là trung điểm của AE

XétΔECA có F là trung điểm của EA

nên CF là đường trung tuyến của ΔECA

Câu c, chứ câu a, b thì kiến thức lớp 7.

Gọi x (km/h) là vận tốc của xe máy (x > 0)

Vận tốc xe ô tô là: x + 20 (km/h)

Quãng đường xe máy đã đi từ lúc xuất phát đến lúc gặp xe ô tô là 120 (km)

Quãng đường xe ô tô đã đi từ lúc xuất phát đến lúc gặp xe máy là: 270 - 120 = 150 (km)

Thời gian xe đi từ A đi đến lúc gặp nhau:

Thời gian ô tô đã đi đến lúc gặp nhau:

Theo đề bài, ta có phương trình:

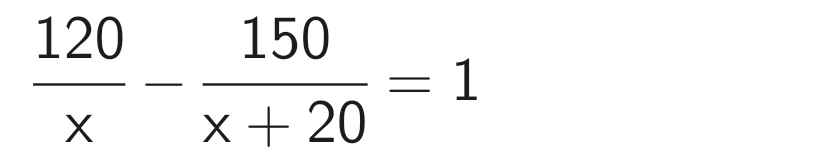
120(x + 20) - 150x = x(x + 20)

120x + 2400 - 150x = x² + 20x

x² + 20x - 120x + 150x - 2400 = 0

x² + 50x - 2400 = 0

x² - 30x + 80x - 2400 = 0

(x² - 30x) + (80x - 2400) = 0

x(x - 30) + 80(x - 30) = 0

(x - 30)(x + 80) = 0

x - 30 = 0 hoặc x + 80 = 0

*) x - 30 = 0

x = 30 (nhận)

*) x + 80 = 0

x = -80 (loại)

Vậy vận tốc xe máy là 30 km/h, vận tốc xe ô tô là 30 + 20 = 50 km/h

Phân số thể hiện số lít dầu còn lại trong thùng 1 là: 

\(1-\dfrac{1}{2}=\dfrac{1}{2}\) (số lít dầu có ở thùng 1 ban đầu) 

Phân số thể hiện số lít dầu còn lại trong thùng 2 là: 

\(1-\dfrac{1}{4}=\dfrac{3}{4}\) (số lít dầu có ở thùng 1 ban đầu) 

Phân số thể hiện số lít dầu còn lại trong thùng 3 là: 

\(1-\dfrac{1}{3}=\dfrac{2}{3}\) (số lít dầu có ở thùng 1 ban đầu) 

Do khi lấy đi \(\dfrac{1}{2}\) thùng 1; \(\dfrac{1}{4}\) thùng 2 và \(\dfrac{1}{3}\) thùng 3 thì số lít dầu còn lại ở mỗi thùng là bằng nhau nên \(\dfrac{1}{2}\) thùng thứ nhất bằng \(\dfrac{3}{4}\) thùng thứ hai \(\dfrac{2}{3}\) thùng thứ ba 

Quy đồng các phân số ta được:  \(\dfrac{6}{12}\) thùng thứ nhất = \(\dfrac{6}{8}\)  thùng thứ hai = \(\dfrac{6}{9}\) thùng thứ ba

Theo tỉ lệ đó, ta có sơ đồ: 

Thùng 1: 12 phần

Thùng 2: 8 phần

Thùng 3: 9 phần

Tổng số phần bằng nhau là: 

`12 + 8 + 9 = 29` (phần) 

Giá trị 1 phần là: 

`232 : 29 = 8` (lít)

Thùng 1 có số lít dầu ban đầu là: 

`8` x `12 = 96` (lít)

Thùng 2 có số lít dầu ban đầu là: 

`8` x `8 = 64` (lít)

Thùng 1 có số lít dầu ban đầu là: 

`8` x `9= 72` (lít)

Đáp số: ....

Bốn lần số thứ nhất là:

99620 - 48080 = 51540

Số thứ nhất là:

51540 : 4 = 12885

Số thứ hai là:

48080 - 12885 = 35195

5,8m>5,799m

0,2m=20cm

0,64m<6,5dm

9,3m>9m3cm

456m>0,45km

67dm4mm<67,4dm

705m<0,75km

8m10mm=8,01m

Anh Thái chuyển bao nhiêu viên bi đi chăng nữa thì tổng số bi ở hai hộp vẫn không đổi

Tổng số viên bi ở hai hộp là: 

`32 + 13 = 45` (viên bi)

Ta có sơ đồ: 

Hộp nhỏ lúc đó: 4 phần

Hộp to lúc đó: 5 phần

Tổng số phần bằng nhau là: 

`4+5=9` (phần)

Giấ trị 1 phần là: 

`45 : 9 = 5` (viên bi)

Hộp to lúc đó có số viên bi là: 

`5` x `5 = 25` (viên)

Anh Thái đã di chuyển số viên bi là: 

`32 - 25 = 7` (viên) 

Đáp số: `7` viên

\(\dfrac{72^3.54^3:8^3}{108^5:4^5}\)

= \(\dfrac{\left(2^3.3^2\right)^3.\left(2.3^3\right)^3:\left(2^3\right)^3}{\left(2^2.3^3\right)^5:\left(2^2\right)^5}\)

= \(\dfrac{2^9.3^6.2^3.3^9:2^9}{2^{10}.3^{15}:2^{10}}\)

= \(\dfrac{3^{15}.2^3}{3^{15}}\)

= `2^3`

Em cảm ơn ạ