Lời giải:
$A=a^2+ab+b^2-3b-3a+3$

$4A=4a^2+4ab+4b^2-12a-12b+12$

$=(4a^2+4ab+b^2)-12a-12b+3b^2+12$

$=(2a+b)^2-6(2a+b)+9+(3b^2-6b+3)$

$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$

Vậy $A_{\min}=0$. Giá trị này đạt tại $2a+b-3=b-1=0$

$\Leftrightarrow b=1; a=1$

Câu B tương tự câu A nhé. Chỉ khác mỗi đặt tên biến.

---------------

$C=x^2+5y^2-4xy+2y-3$

$=(x^2-4xy+4y^2)+(y^2+2y)-3$

$=(x-2y)^2+(y^2+2y+1)-4$

$=(x-2y)^2+(y+1)^2-4\geq 0+0-4=-4$

Vậy $C_{\min}=-4$. Giá trị này đạt tại $x-2y=y+1=0$

$\Leftrightarrow y=-1; x=-2$

Đáp án: A

Giải thích các bước giải:

 Số ngày lớn nhất trong một tháng là 31, và các số nguyên tố có hai chữ số nhỏ nhất là 11, 13, 17 (các số nguyên tố tiếp theo bị loại vì tổng của nó với số nguyên tố có hai chữ số bất kỳ lớn hơn 31).

Vậy ba số áo 11, 13, 17, và ba tổng đôi một của chúng là 24, 28 và 30.

Vì tất cả các ngày nói đến trong câu chuyện nằm trong cùng một tháng, nên ngày sinh của Caitlin lớn nhất, tức là bằng 30, ngày hôm nay là 28 và ngày sinh của Bethany là 24.

Từ đó dễ dàng tìm được số áo của Asley là 13, của Bethany là 17 còn Caitlin mang áo số 11.

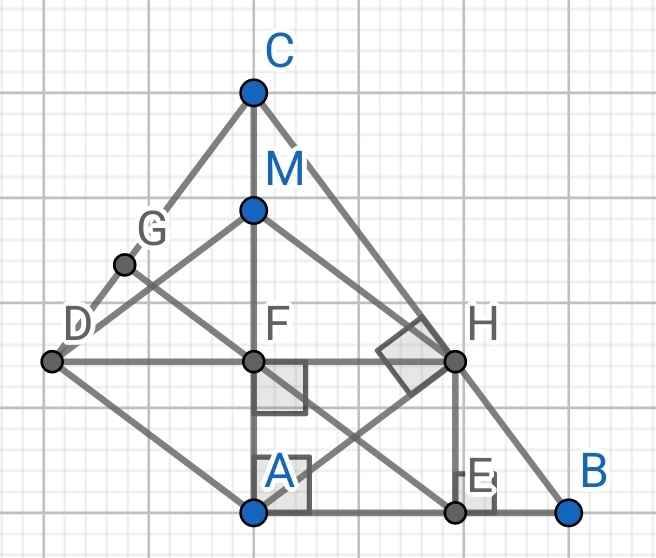 a) Do HE ⊥ AB (gt)

⇒ ∠AEH = 90⁰

Do HF ⊥ AC (gt)

⇒ ∠AFH = 90⁰

Do ∆ABC vuông tại A (gt)

⇒ ∠EAF = 90⁰

Tứ giác AEHF có:

∠AEH = ∠AFH = ∠EAF = 90⁰

⇒ AEHF là hình chữ nhật

b) Do AEHF là hình chữ nhật (cmt)

⇒ HE = AF

Mà AF = FM (do A và M đối xứng qua F)

⇒ HE = FM

Do AEHF là hình chữ nhật (cmt)

⇒ HE // AF

⇒ HE // FM

Tứ giác EFMH có:

HE // FM (cmt)

HE = FM (cmt)

⇒ EFMH là hình bình hành

c) Do A và M đối xứng qua F (gt)

⇒ F là trung điểm của AM

Do D và H đối xứng qua F (gt)

⇒ F là trung điểm của DH

Do HF ⊥ AC (gt)

⇒ HD ⊥ AM

Tứ giác AHMD có:

F là trung điểm của AM (cmt)

F là trung điểm của DH (cmt)

⇒ AHMD là hình bình hành

Mà HD ⊥ AM (cmt)

⇒ AHMD là hình chữ thoi

⇒ AD // MH

Do EFMH là hình bình hành (cmt)

⇒ EF // MH

Mà AD // MH

⇒ EF // AD

Do ADMH là hình thoi (cmt)

⇒ AM là tia phân giác của ∠DAH

⇒ ∠DAM = ∠HAM

⇒ ∠DAC = ∠HAC

Do ADMH là hình thoi

⇒ AD = AH

Xét ∆ADC và ∆AHC có:

AD = AH (cmt)

∠DAC = ∠HAC (cmt)

AC là cạnh chung

⇒ ∆ADC = ∆AHC (c-g-c)

⇒ ∠ADC = ∠AHC = 90⁰ (hai góc tương ứng)

⇒ AD ⊥ DC

Mà EF // AD (cmt)

⇒ EF ⊥ DC

Lời giải:

$x^3+y^3=(x+y)^3-3xy(x+y)=2^3-3xy.2=8-6xy$

$=8-3.2xy=8-3[(x+y)^2-(x^2+y^2)]=8-3(2^2-34)=98$

----------------

$x^4+y^4=(x^2+y^2)^2-2x^2y^2=34^2-\frac{1}{2}(2xy)^2$

$=34^2-\frac{1}{2}[(x+y)^2-(x^2+y^2)]^2=34^2-\frac{1}{2}(2^2-34)^2=706$

Đề sai, em xem lại đề nhé

Bài 3

a) 2x(x - 3) - x + 3 = 0

2x(x - 3) - (x - 3) = 0

(x - 3)(2x - 1) = 0

x - 3 = 0 hoặc 2x - 1 = 0

*) x - 3 = 0

x = 3

*) 2x - 1 = 0

2x = 1

x = 1/2

Vậy x = 1/2; x = 3

b) (3x - 1)(2x + 1) - (x + 1)² = 5x²

6x² + 3x - 2x - 1 - x² - 2x - 1 - 5x² = 0

(6x² - x² - 5x²) + (3x - 2x - 2x) = 0 + 1 + 1

-x = 2

x = -2

Bài 2

a) 5x² + 30y

= 5(x² + 6y)

b) x³ - 2x² - 4xy² + x

= x(x² - 2x - 4y² + 1)

= x[(x² - 2x + 1) - 4y²]

= x[(x - 1)² - (2y)²]

= x(x - 1 - 2y)(x - 1 + 2y)