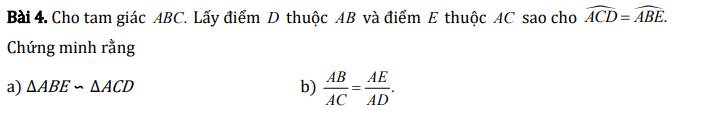
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có:
M là trung điểm của AB
N là trung điểm của AC
⇒ MN là đường trung bình của tam giác ABC
⇒ MN // BC
\(\Rightarrow\widehat{AMN}=\widehat{ABC}\) (đồng vị)
Xét hai tam giác ABC và AMN có:
\(\widehat{AMN}=\widehat{ABC}\left(cmt\right)\)
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta ABC\sim\Delta AMN\left(g.g\right)\)
b) Chứng minh tương tự như câu a thì ta có:
PN cũng là đường trung bình của tam giác ABC \(\Rightarrow PN=\dfrac{1}{2}AB\)
PM cũng là đường trung bình của tam giác ABC \(\Rightarrow PM=\dfrac{1}{2}AC\)
Mà: \(NM=\dfrac{1}{2}BC\) (NM là đường trung bình ...)
Xét hai tam giác ABC và PNM có:
\(\dfrac{PN}{AB}=\dfrac{PM}{AC}=\dfrac{NM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta PNM\left(c.c.c\right)\)

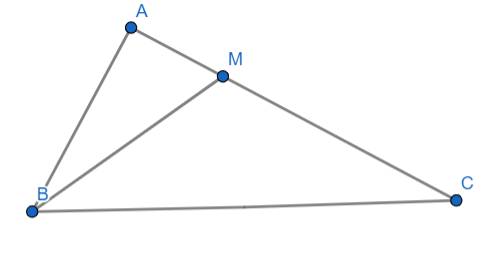
a) Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{10^2+20^2}=10\sqrt{5}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABM vuông tại A ta có:
\(BM^2=AB^2+AM^2\)
\(\Rightarrow BM=\sqrt{AB^2+AM^2}\)
\(\Rightarrow BM=\sqrt{10^2+5^2}=5\sqrt{5}\left(cm\right)\)
b) Ta có:
\(\dfrac{AM}{AB}=\dfrac{1}{2}\)
\(\dfrac{BM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
Xét hai tam giác ABC và AMB có:
\(\widehat{BAC}\) chung
\(\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta AMB\left(c.g.c\right)\)

Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Ta có:
\(\dfrac{AB}{DE}=\dfrac{3}{15}=\dfrac{1}{5}\)
\(\dfrac{AC}{DF}=\dfrac{4}{20}=\dfrac{1}{5}\)
\(\dfrac{BC}{EF}=\dfrac{5}{25}=\dfrac{1}{5}\)
\(\Rightarrow\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{EF}=\dfrac{1}{5}\)
Xét hai tam giác ABC và DEF có:
\(\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{EF}\left(=\dfrac{1}{5}\right)\)
\(\Rightarrow\Delta ABC\sim\Delta DEF\left(c.c.c\right)\)

Lời giải:
$\frac{2x+3}{4-x^2}=\frac{-(2x+3)}{x^2-4}=\frac{-(2x+3)}{(x-2)(x+2)}=\frac{-(2x+3)(x-2)}{(x-2)^2(x+2)}=\frac{-(2x^2-x-6)}{(x-2)^2(x+2)}$
$\frac{5x-4}{x^2-4x+4}=\frac{(5x-4)(x+2)}{(x^2-4x+4)(x+2)}=\frac{5x^2+6x-8}{(x-2)^2(x+2)}$

Chứng minh bằng biến đổi tương đương:
\(x^8+y^8\ge x^2y^2\left(x^4+y^4\right)\)
\(\Leftrightarrow x^8-x^6y^2+y^8-x^2y^6\ge0\)
\(\Leftrightarrow x^6\left(x^2-y^2\right)-y^6\left(x^2-y^2\right)\ge0\)
\(\Leftrightarrow\left(x^6-y^6\right)\left(x^2-y^2\right)\ge0\)
\(\Leftrightarrow\left[\left(x^2\right)^3-\left(y^2\right)^3\right]\left(x^2-y^2\right)\ge0\)
\(\Leftrightarrow\left(x^2-y^2\right)\left(x^4+x^2y^2+y^4\right)\left(x^2-y^2\right)\ge0\)
\(\Leftrightarrow\left(x^2-y^2\right)^2\left(x^4+x^2y^2+y^4\right)\ge0\) (luôn đúng với mọi x;y)
Vậy BĐT đã cho được chứng minh.

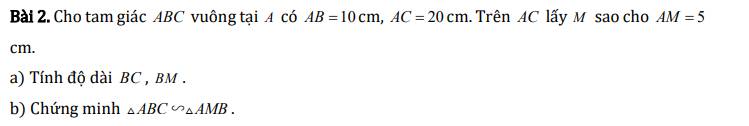
a) Xét hai tam giác ABE và ACD có:
\(\widehat{ACD}=\widehat{ABE}\left(gt\right)\)
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta ABE\sim\Delta ACD\left(g.g\right)\)
b) Ta có: \(\Delta ABE\sim\Delta ACD\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AD}\)