\(A=\dfrac{2024^{30}+1}{2024^{29}+1}\\ B=\dfrac{2024^{29}+1}{2024^{28}+1}\) SO SÁNH BÀI BÊN GIÚP MIK VỚI Ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích hình chữ nhật là \(345\cdot295=101775\left(m^2\right)\)

\(P=\dfrac{200}{2}+\dfrac{200}{6}+...+\dfrac{200}{9900}\)
\(=200\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{9900}\right)\)
\(=200\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\right)\)
\(=200\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=200\left(1-\dfrac{1}{100}\right)=200\cdot\dfrac{99}{100}=198\)


Bài 4
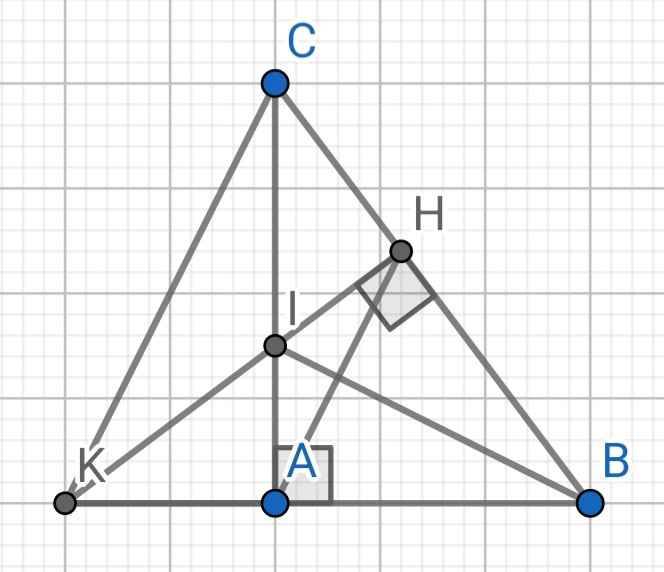
a) Do AB < AC < BC (6 < 8 < 10)
⇒ ∠ACB < ∠ABC < ∠BAC
b) Do BI là tia phân giác của ∠ABC (gt)
⇒ ∠ABI = ∠CBI
⇒ ∠ABI = ∠HBI
Xét hai tam giác vuông: ∆ABI và ∆HBI có:
BI là cạnh chung
∠ABI = ∠HBI (cmt)
⇒ ∆ABI = ∆HBI (cạnh huyền - góc nhọn)
c) Do ∆ABI = ∆HBI (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABI = ∆HBI (cmt)
⇒ AI = HI (hai cạnh tương ứng)
⇒ I nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BI là đường trung trực của AH
d) ∆CHI vuông tại H
⇒ IC là cạnh huyền nên CI là cạnh lớn nhất
⇒ HI < IC
Mà HI = IA (cmt)
⇒ IA < IC
e) ∆ABC vuông tại A (gt)
⇒ CA ⊥ AB
⇒ CA ⊥ BK
⇒ CA là đường cao của ∆BCK
Do IH ⊥ BC (gt)
⇒ KH ⊥ BC
⇒ KH là đường cao của ∆BCK
∆BCK có:
CA là đường cao (cmt)
KH là đường cao (cmt)
Mà I là giao điểm của CA và KH
⇒ BI là đường cao thứ ba của ∆BCK
⇒ BI KC
f) Xét hai tam giác vuông: ∆AIK và ∆HIC có:
AI = HI (cmt)
∠AIK = ∠HIC (đối đỉnh)
⇒ ∆AIK = ∆HIC (cạnh góc vuông - góc nhọn kề)
⇒ IK = IC (hai cạnh tương ứng)
Bài 3:
a: Xét ΔBAK và ΔBIK có
BA=BI
\(\widehat{ABK}=\widehat{IBK}\)
BK chung
Do đó: ΔBAK=ΔBIK
b: Ta có: ΔBAK=ΔBIK
=>\(\widehat{BAK}=\widehat{BIK}\)
=>\(\widehat{BIK}=90^0\)
=>KI\(\perp\)BC
Ta có: ΔBAK=ΔBIK
=>KA=KI
mà KI<KC(ΔKIC vuông tại I)
nên KA<KC
c: Ta có: \(\widehat{CAI}+\widehat{BAI}=\widehat{BAC}=90^0\)
\(\widehat{HAI}+\widehat{BIA}=90^0\)(ΔHAI vuông tại H)
mà \(\widehat{BAI}=\widehat{BIA}\)(ΔBAI cân tại B)
nên \(\widehat{CAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAC
d: Ta có: BA=BI
=>B nằm trên đường trung trực của AI(1)
Ta có: KA=KI
=>K nằm trên đường trung trực của AI(2)
Từ (1) và (2) suy ra BK là đường trung trực của AI
=>BK\(\perp\)AI
Xét ΔBAI có
BK,AH là các đường cao
BK cắt AH tại O
Do đó: O là trực tâm của ΔBAI
=>IO\(\perp\)BA
mà IM\(\perp\)AB
và IM,IO có điểm chung là I
nên I,M,O thẳng hàng
Bài 5:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Ta có: ΔABM=ΔACM
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Ta có: AE=AF
=>A nằm trên đường trung trực của EF(1)
Ta có: KE=KF
=>K nằm trên đường trung trực của FE(2)
Ta có: ME=MF(ΔAEM=ΔAFM)
=>M nằm trên đường trung trực của FE(3)
Từ (1),(2),(3) suy ra A,K,M thẳng hàng
d:
Ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
Ta có: AM\(\perp\) BC
AM//DC
Do đó: DC\(\perp\)BC
Ta có: \(\widehat{ACD}+\widehat{ACB}=\widehat{DCB}=90^0\)
\(\widehat{ADC}+\widehat{ABC}=90^0\)(ΔDCB vuông tại C)
mà \(\widehat{ACB}=\widehat{ABC}\)(ΔABC cân tại A)
nên \(\widehat{ACD}=\widehat{ADC}\)
=>AC=AD
mà AB=AC
nên AB=AD
=>A là trung điểm của BD

Ta có: ΔSAD đều
mà SH là đường trung tuyến
nên SH\(\perp\)AD
Ta có: (SAD)\(\perp\)(ABCD)
\(\left(SAD\right)\cap\left(ABCD\right)=AD\)
SH\(\perp\)AD
Do đó: SH\(\perp\)(ABCD)
mà \(SH\subset\left(SHB\right)\)
nên \(\left(SHB\right)\perp\left(ABCD\right)\)

3/4 + 5/4 = 8/4
35/25 + 7/25 = 42/25
9/4 + 3/5 = 45/20 + 12/20=57/20
3/5 + 4/3 = 9/15 + 20/15 = 29/15
3/8 + 7/6 = 9/24 + 28/24 = 37/24
2/3 + 3/4 = 8/12 + 9/12 = 17/12
2/5 + 4/7 = 14/35 + 20/35 = 34/35
3/12 + 1/4 = 3/12 + 3/12 = 6/12 = 1/2
3/4 + 5/4 = 8/4 = 2
35/25 + 7/25 = 42/25
9/4 + 3/5 = 45/20 + 12/20 = 57/20
3/5 + 4/3 = 9/15 + 20/15 = 29/15
3/8 + 7/6 = 9/24 + 28/24 = 37/24
2/3 + 3/4 = 9/12 + 9/12 = 17/12
2/5 + 4/7 = 14/35 + 20/35 = 34/35
3/12 + 1/4 = 1/4 + 1/4 = 2/4 = 1/2
\(\dfrac{A}{2024}=\dfrac{2024^{30}+1}{2024^{30}+2024}=1-\dfrac{2023}{2024^{30}+2024}\)
\(\dfrac{B}{2024}=\dfrac{2024^{29}+1}{2024^{29}+2024}=1-\dfrac{2023}{2024^{29}+2024}\)
\(2024^{30}+2024>2024^{29}+2024\)
=>\(\dfrac{2023}{2024^{30}+2024}< \dfrac{2023}{2024^{29}+2024}\)
=>\(-\dfrac{2023}{2024^{30}+2024}>-\dfrac{2023}{2024^{29}+2024}\)
=>\(1-\dfrac{2023}{2024^{30}+2024}>1-\dfrac{2023}{2024^{29}+2024}\)
=>\(\dfrac{A}{2024}>\dfrac{B}{2024}\)
=>A>B