5 + 5 mũ 3 + 5 mũ 5 + 5 mũ 7 +...+5 mũ 99
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tứ giác AMCN có hai đường chéo AC và MN vuông góc với nhau tại trung điểm của mỗi đường.
Thật vậy ta có:
\(AC\perp BD\Rightarrow AC\perp MN\)
\(\left\{{}\begin{matrix}HA=HC\\HB=HD\end{matrix}\right.\) hai đường chéo hình vuông thì vuông góc tại trung điểm của mỗi đường.
\(HB=HD\Rightarrow DN+NH=BM+MH\Rightarrow NH=MH\)
Vậy tứ giác AMCN là hình thoi.
Diện tích hình thoi AMCN là:
\(S_{AMCN}=\dfrac{1}{2}AC.MN=\dfrac{1}{2}AC.BD.\dfrac{1}{3}\\ =S_{ABCD}.\dfrac{1}{3}=\dfrac{1}{3}.12.12=48cm^2\)
Đs....

17x2y chia hết cho 2,5,3
Số chia hết cho cả 2 và 5 là những số có tận cùng là 0
=> y=0
Tổng các chữ số hiện giờ là: 17x20=1+7+x+2+0=1+7+0+2+0=10(coi x=0)
Mà 12,15,18 đều chia hết cho 3
=> xE{2;5;8}
Vậy y=0; xE{2;5;8}
\(\overline{17x2y}\) ⋮ 2,3,5 ⇔ \(\left\{{}\begin{matrix}y=0\\1+7+x+2+y⋮3\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}y=0\\x+10⋮3\end{matrix}\right.\) \(\Leftrightarrow\)\(\left\{{}\begin{matrix}y=0\\\left[{}\begin{matrix}x=2\\x=5\\x=8\end{matrix}\right.\end{matrix}\right.\)
vậy các số thỏa mãn đề bài: 17220; 17520; 17820

`2^x +2^x =48`
`2^x (1+1)=48`
`2^x *2 =48`
`2^x = 48/2 =24`
`=> x in emptyset`
2x + 2x = 48
2x. ( 1 + 1 ) = 48
2x.2 = 48
2x = 48 : 2
2x = 24
x = log224


\(n+3⋮n-2\\ =>n-2+5⋮n-2\\ =>n-2\inƯ\left(5\right)\)
\(Ư\left(5\right)=\left\{1;-1;5;-5\right\}\)
\(=>\left\{{}\begin{matrix}n-2=-1\\n-2=1\\n-2=5\\n-2=-5\end{matrix}\right.=>\left\{{}\begin{matrix}n=1\\n=3\\n=7\\n=-3\end{matrix}\right.\)
\(\dfrac{n+3}{n-2}=1+\dfrac{5}{n-2}\)
Để n+3 chia hết cho n-2 thì 5 phải chia hết cho n- 2. Hay \(n-2=\pm5\) hoặc \(n-2=\pm1\)
Vậy: n =\(\left\{-3;1;3;7\right\}\)

`28 . x - x . 17 - x = 250`
`x*(28-17-1)=250`
`x* 10=250`
`x =250/10=25`
Vậy `x=25`

\(568-\left\{5.\left[143-\left(4-1\right)^2\right]+10\right\}\cdot1\)
\(\Rightarrow568-\left\{5\cdot\left[143-3^2\right]+10\right\}\)
\(\Rightarrow568-\left\{5\cdot\left\{143-9\right\}+10\right\}\)
\(\Rightarrow568-\left\{5\cdot134+10\right\}\)
\(\Rightarrow568-\left\{670+10\right\}\)
\(\Rightarrow568-680\)
\(\Rightarrow-112\)
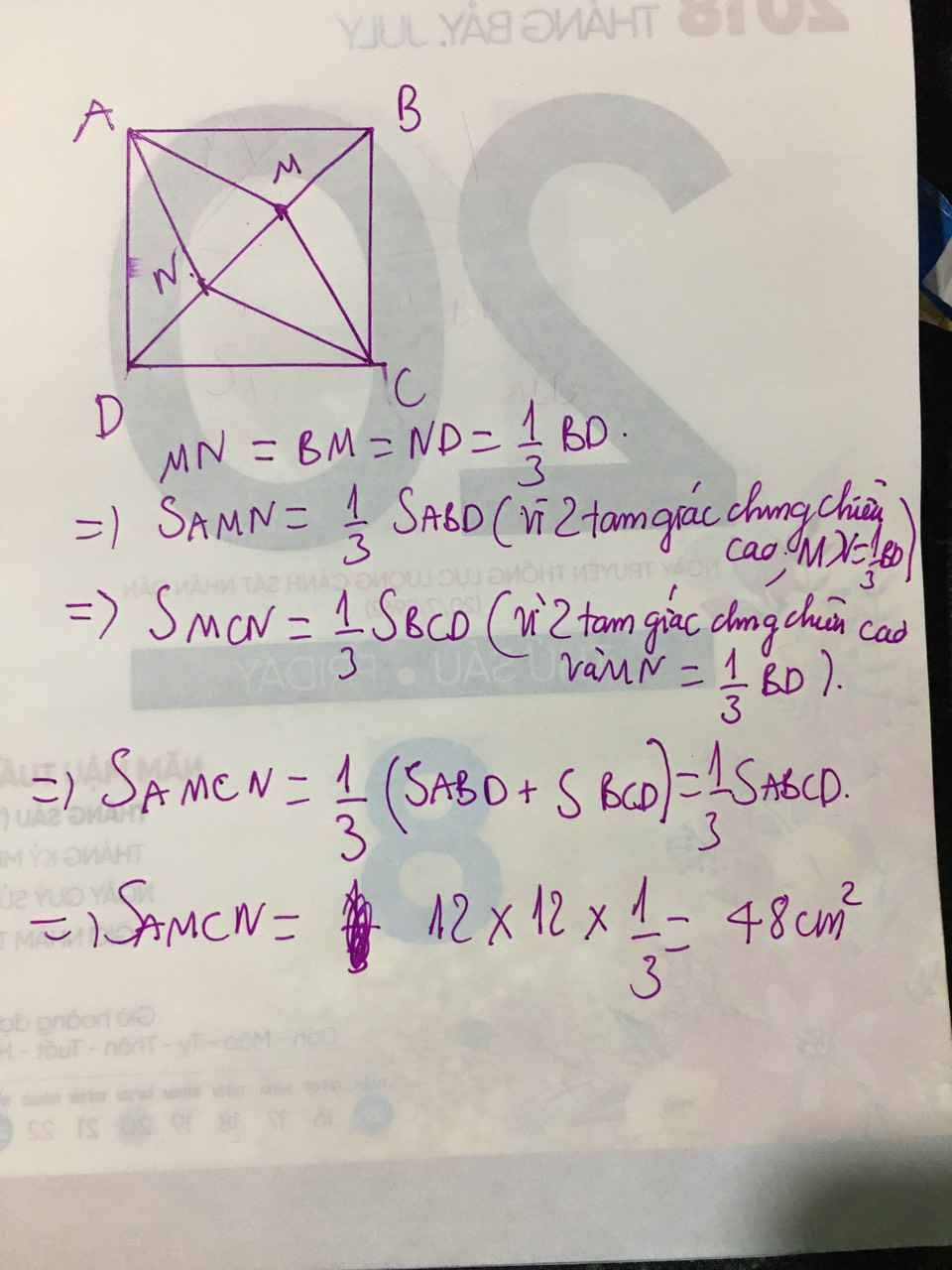
Đặt A = 5 + 53 + 55 + 57 + ... + 599
52A = 53 + 55 + 57 + 59 + ... + 5101
25A - A = ( 53 + 55 + 57 + 59 + ... + 5101 ) - ( 5 + 53 + 55 + 57 + ... + 599 )
24A = 5101 - 5
A = \(\dfrac{5^{101}-5}{24}\)