Quy đồng mẫu số: 9/14 và 33/69.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Đặt F=C*x+b
Thay x=0 và F=32 vào F=Cx+b, ta được:
\(0\cdot C+b=32\)
=>b=32
=>F=Cx+32
Thay x=1 và y=32+1,8=33,8 vào F=x*C+32, ta được:
\(x\cdot1+32=33,8\)
=>x+32=33,8
=>x=1,8
Vậy: F=1,8C+32
b: Nước sôi ở nhiệt độ 100 độ C
=>\(F=1,8\cdot100+32=180+32=212^0F\)

Xét ΔAHB và ΔAHC có
AB=AC
\(\widehat{BAH}=\widehat{CAH}\)
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
=>AH\(\perp\)BC

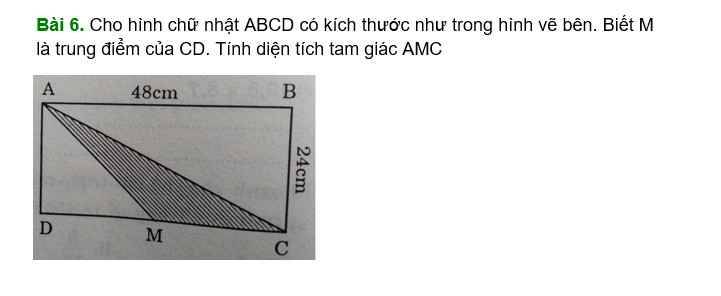
Diện tích hình chữ nhật ABCD là \(48\cdot24=1152\left(cm^2\right)\)
=>Diện tích tam giác ADC là \(\dfrac{1152}{2}=576\left(cm^2\right)\)
Vì M là trung điểm của DC nên \(S_{AMC}=\dfrac{1}{2}\cdot S_{ADC}=\dfrac{1}{2}\cdot576=288\left(cm^2\right)\)

a: Ta có; ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100=10^2\)
=>BC=10(cm)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{6}=\dfrac{CD}{10}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{5}\)
mà AD+CD=AC=8cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{5}=\dfrac{AD+CD}{3+5}=\dfrac{8}{8}=1\)
=>\(AD=3\cdot1=3\left(cm\right)\)
b: Vì BD là phân giác trong tại B của ΔABC
và BD\(\perp\)BE
nênBE là phân giác ngoài tại B của ΔABC
Xét ΔABC có BE là phân giác ngoài tại B
nên \(\dfrac{EA}{EC}=\dfrac{AB}{BC}\)
mà \(\dfrac{AB}{BC}=\dfrac{DA}{DC}\)
nên \(\dfrac{EA}{EC}=\dfrac{DA}{DC}\)
=>\(EA\cdot DC=DA\cdot EC\)

\(x\) - \(\dfrac{1}{7}\) = \(\dfrac{-6}{21}\)
\(x\) = \(\dfrac{-6}{21}\) + \(\dfrac{1}{7}\)
\(x\) = - \(\dfrac{1}{7}\)
\(\dfrac{x-1}{7}=\dfrac{-6}{21}\)
=>\(\dfrac{x-1}{7}=\dfrac{-2}{7}\)
=>x-1=-2
=>x=-2+1=-1

Tổng số phần bằng nhau là 1+3=4(phần)
Số học sinh nam là \(32:4\cdot1=8\left(bạn\right)\)
=>Tỉ số phần trăm giữa số học sinh nam và số học sinh cả lớp là \(\dfrac{8}{32}=25\%\)

a: Đáy bé hình thang là \(40\cdot30\%=12\left(cm\right)\)
Diện tích hình thang là \(\dfrac{1}{2}\cdot\left(40+12\right)\cdot12=6\cdot52=312\left(cm^2\right)\)
b:
Ta có: AB//CD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}=\dfrac{3}{10}\)
Vì OA/OC=3/10
nên \(S_{OAB}=\dfrac{3}{10}\cdot S_{BOC}\)
Vì \(\dfrac{OB}{OD}=\dfrac{3}{10}\)
nên \(S_{OAB}=\dfrac{3}{10}\cdot S_{AOD}\)
=>\(S_{BOC}=S_{AOD}\)
=>\(S_{BOC}+S_{OAB}=S_{AOD}+S_{OAB}\)
=>\(S_{ABC}=S_{ABD}\)
Ta có: \(S_{BOC}=S_{AOD}\)
=>\(S_{BOC}+S_{COD}=S_{AOD}+S_{COD}\)
=>\(S_{BCD}=S_{ADC}\)


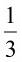
\(\dfrac{33}{69}\) = \(\dfrac{11}{23}\) = \(\dfrac{154}{322}\)
\(\dfrac{9}{14}\) = \(\dfrac{9\times23}{14\times23}\) = \(\dfrac{207}{322}\)
Vậy các phân số \(\dfrac{9}{14}\) và \(\dfrac{33}{69}\) đã được quy đồng mẫu số các phân số thành các phân số:
\(\dfrac{207}{322}\); \(\dfrac{154}{322}\);
\(\dfrac{9}{14}=\dfrac{9\cdot69}{14\cdot69}=\dfrac{621}{966}\)
\(\dfrac{33}{69}=\dfrac{33\cdot14}{69\cdot14}=\dfrac{462}{966}\)