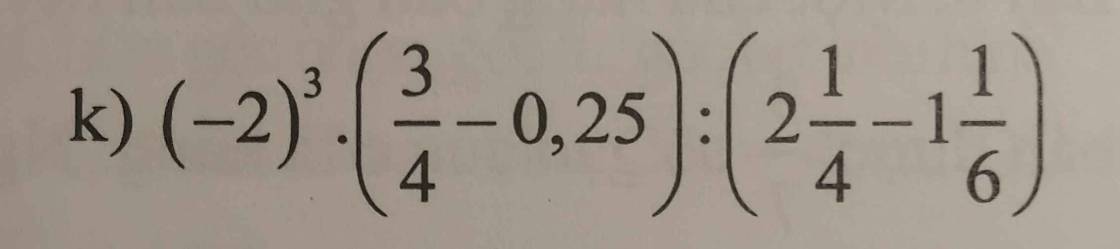\(\left(-2\right)^3\cdot\left(\dfrac{3}{4}-0,25\right):\left(2\dfrac{1}{4}-1\dfrac{1}{6}\right)\)

\(=-8\left(\dfrac{3}{4}-\dfrac{1}{4}\right):\left(\dfrac{9}{4}-\dfrac{7}{6}\right)\)

\(=-8\cdot\dfrac{2}{4}:\left(\dfrac{27}{12}-\dfrac{14}{12}\right)\)

\(=-4:\dfrac{13}{12}=-4\cdot\dfrac{12}{13}=-\dfrac{48}{13}\)

K; (-2)³.(\(\dfrac{3}{4}\) - 0,25): (2\(\dfrac{1}{4}\) - 1\(\dfrac{1}{6}\))

 = - 8.(0,75 - 0,25): (\(\dfrac{9}{4}-\dfrac{7}{6}\))

= - 8.0,5 : \(\dfrac{13}{12}\)

= - 4 : \(\dfrac{13}{12}\)

= - \(\dfrac{48}{13}\) 

Lời giải:

Gọi số thứ hai là $b$ thì số thứ ba là $\overline{1b}$. Số thứ nhất là $2\times \overline{1b}$.
Tổng của ba số là:

$2\times \overline{1b}+b+\overline{1b}=18\times 3=54$

$3\times \overline{1b}+b=54$

Nếu $b$ là số có 2 chữ số trở lên thì $\overline{1b}$ có từ 3 chữ số trở lên

Khi đó tổng $3\times \overline{1b}+b$ không thể nhỏ hơn 100. Mà 54< 100 nên loại

Vậy $b$ có 1 chữ số. Khi đó:

$3\times \overline{1b}+b=54$

$3\times (10+b)+b=54$

$30+3\times b+b=54$

$30+4\times b=54$

$4\times b=24$

$b=24:4=6$

Vậy 3 số cần tìm là: $32; 6; 16$

Cc

Tỉ số giữa số ô tô và số siêu nhân là 8/5

Tổng số phần bằng nhau là 8+5=13(phần)

Số ô tô là 403:13x8=248

Số siêu nhân là 403-248=155

...↓

Ta có:

1×2×3×4×5 = 120 có chữ số tận cùng là 0

Tích bắt đầu từ thừa số 5 luôn có chữ số tận cùng là 0

Vậy không thể tìm được tích có chữ số tận cùng là 9