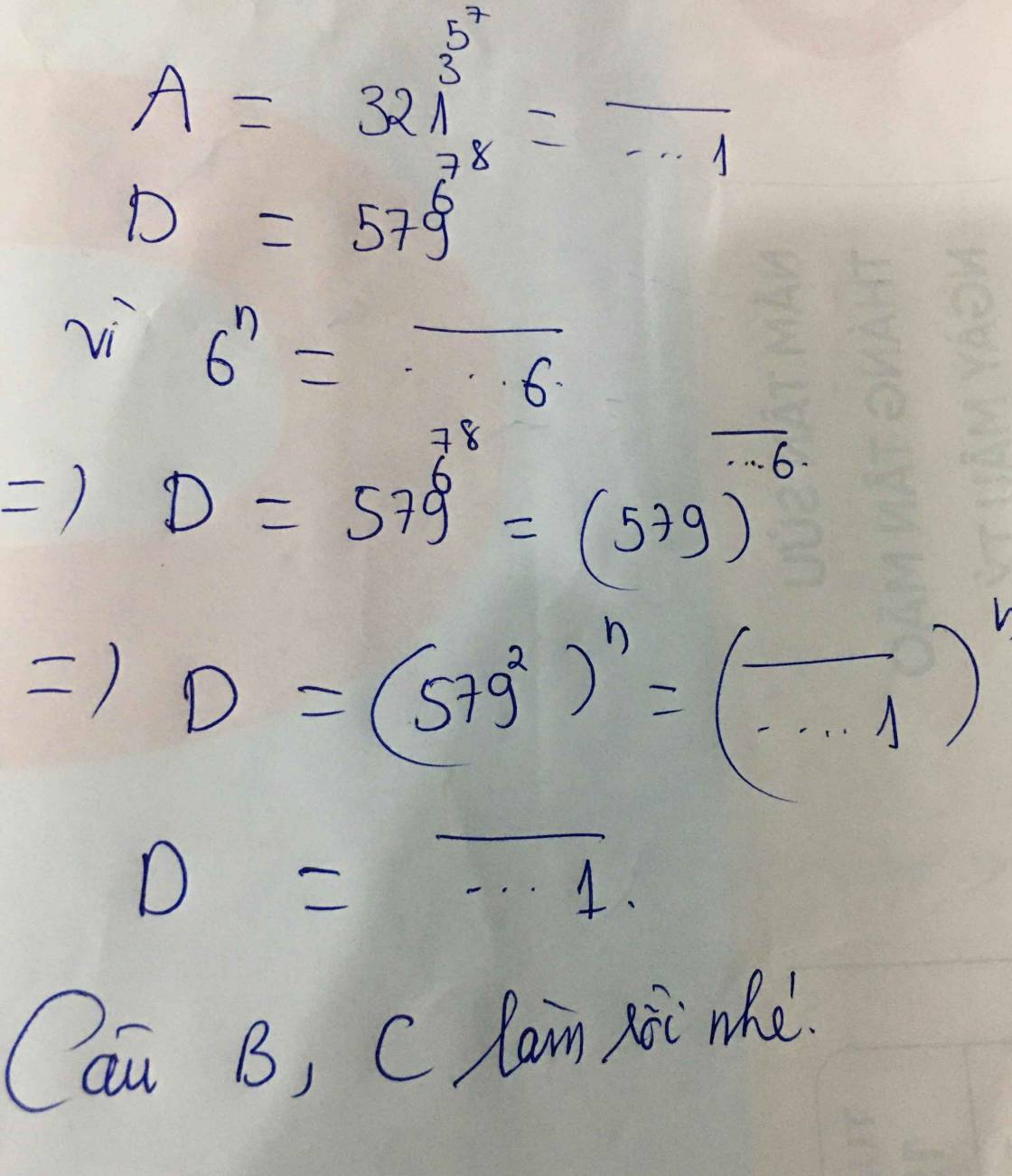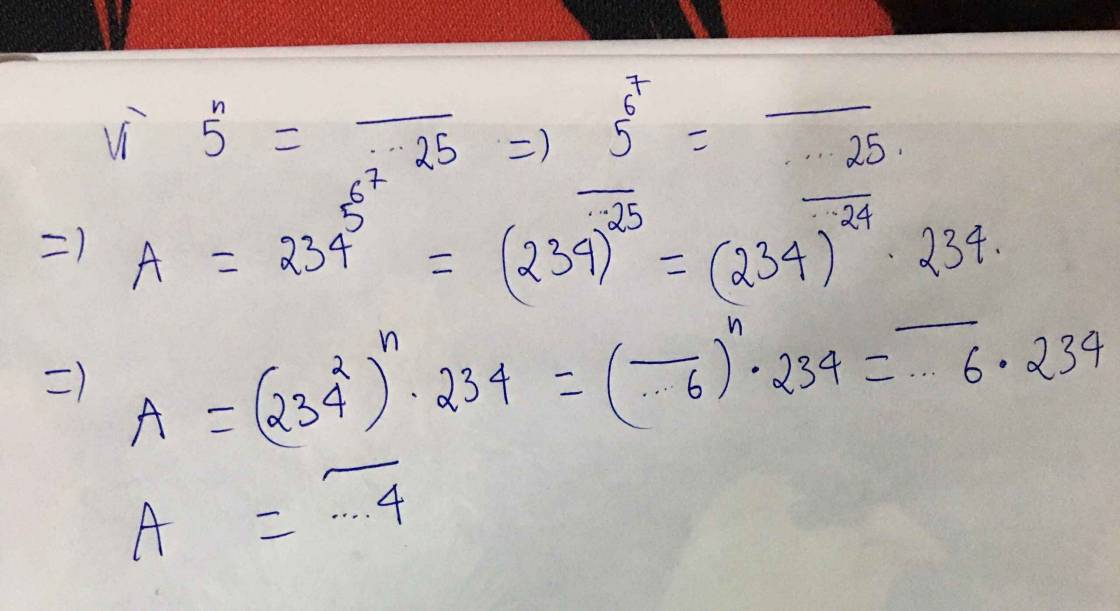
A = 64²⁷ = (64²)¹³.64 = (\(\overline{...6}\))¹³.64 = \(\overline{...6}\) .64 = \(\overline{...4}\) 

B =  19²⁰ = (19²)¹⁰ = \(\overline{...1}\)¹⁰ = \(\overline{...1}\)

C = 114⁴⁴ = (114²)²² = \(\overline{...6}\)¹¹ =  \(\overline{...6}\)

D = 99⁹⁹ = ( 99²)⁴⁹.99 = \(\overline{...1}\)⁴⁹.99 = \(\overline{...9}\)

E = 53⁴⁵ = ( 53⁴)¹¹.53 = \(\overline{...6}\)¹¹. 53  = \(\overline{...6}\).53 = \(\overline{..8}\)

G = 234⁵ = (234²)².234 = \(\overline{..6}\)² .234 = \(\overline{...6}\). 234 = \(\overline{...4}\)

H = (579⁶)³⁵ = (579²)¹⁰⁵ = \(\overline{...1}\)¹⁰⁵ = \(\overline{....1}\)

Lời giải:
$x^5+x-1=(x^5+x^2)-(x^2-x+1)$

$=x^2(x^3+1)-(x^2-x+1)=x^2(x+1)(x^2-x+1)-(x^2-x+1)$

$=(x^2-x+1)[x^2(x+1)-1]=(x^2-x+1)(x^3+x^2-1)$

A = \(-\dfrac{1}{9}\) . (-\(\dfrac{3}{5}\))  - \(\dfrac{5}{6}\) . (-\(\dfrac{3}{5}\)) + \(\dfrac{5}{2}\).(-\(\dfrac{3}{5}\))

A = - \(\dfrac{3}{5}\).( \(-\dfrac{1}{9}\) - \(\dfrac{5}{6}\) + \(\dfrac{5}{2}\))

A = - \(\dfrac{3}{5}\).  \(\dfrac{-2-15+45}{18}\)

A = - \(\dfrac{3}{5}\) . \(\dfrac{28}{18}\)

A = - \(\dfrac{14}{15}\)

   S    = 1 +  3 + 3² + 3³ +...+3⁹

3.S    =       3 + 3² + 3³ +....+3⁹+3¹⁰

3S-S = 3¹⁰ - 1

2S    =  3¹⁰ - 1

 S     = \(\dfrac{3^{10}-1}{2}\)      

S  = 3+ 3² + 3³ + 3⁴ +.....+ 3²⁰²²

Xét dãy số : 1; 2; 3; 4; .....;2022

Dãy số trên có số số hạng : ( 2022 -1) : 1 + 1 = 2022 ( số hạng)

mà 2022 ⋮ 3

Vậy nhóm ba số hạng liên tiếp của tổng S thành một nhóm ta được:

S =(3 + 3²+ 3³)+ ( 3⁴ + 3⁵ + 3⁶)+....+( 3²⁰²⁰+3²⁰²¹+3²⁰²²)

S = 3.( 1 + 3 + 3²)+ 3⁴.( 1+3+3²)+....+3²⁰²⁰.(1+3+3²)

S = 3.13 + 3⁴.13+ ^......+3²⁰²⁰.13

S = 13.( 3 + 3⁴+....+3²⁰²⁰)

13⋮ 13 ⇒ 13. ( 3+3⁴+....+3²⁰²⁰) ⋮ 13

 ⇒ S = 3+3²+3³+3⁴+...+3²⁰²²⋮13 (đpcm)

(x+1) + (x+3) + (x+5) +.......+(x+55) = 784

Dãy số trên là dãy số cách đều khoảng cách :

x + 3 - x - 1 = 2

Dãy số trên có số số hạng :

( x +55 - x - 1) : 2 + 1 = 28

(x+ 55+ x +1). 28: 2 = 784

(2x + 56). 14 = 784

2x + 56 = 784 : 14

2x + 56 = 56

2x = 56- 56

2x = 0

x =  0

\(\left(x+1\right)+\left(x+3\right)+\left(x+5\right)+...+\left(x+55\right)=784\)

\(x+1+x+3+x+5+...+x+55=784\)

\(\left(x+x+...+x\right)+\left(1+3+5+...+55\right)=784\)

\(27x+784=784\)

\(27x=0\)

\(x=0\)

`2022xx2023-2022xx1024+2022`

`=2022xx(2023-1024+1)`

`=2022xx1000`

`=2022000`