1/7 rút gọn bằng bao nhiêu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{28}{15}\) x \(\frac{1}{4^2}\) x 3 + (\(\frac{8}{15}\) - \(\frac{69}{60}\) x (-\(\frac{51}{54}\)))
= \(\frac{7}{60}\) x 3 + \(\frac{8}{15}\) + \(\frac{391}{360}\)
= \(\frac{7}{20}\) + \(\frac{8}{15}\) + \(\frac{391}{360}\)
= \(\frac{126}{360}\) + \(\frac{192}{360}\) + \(\frac{391}{360}\)
= \(\frac{318}{360}\) + \(\frac{391}{360}\)
= \(\frac{709}{360}\)

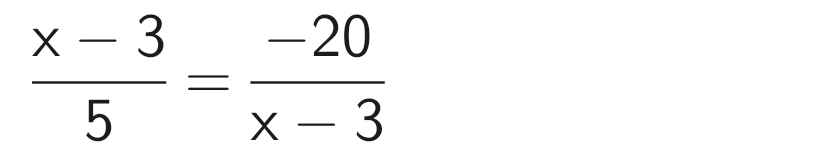 (x - 3).(x - 3) = -20.5
(x - 3).(x - 3) = -20.5
(x - 3)² = -100 (vô lý)
Vậy không tìm được x thỏa mãn yêu cầu đề bài
\(\frac{x-3}{5}\) = \(-\frac{20}{x-3}\)
(\(x-3\)).(\(x-3\)) = -20.5
(\(x-3\))\(^2\) = - 100
(\(x-3)^2\) ≥ 0 > -100 ∀ \(x\)
Không có giá trị nào của \(x\) thỏa mãn đề bài.
Kết luận: \(x\) \(\in\) ∅

Giải:
Số có hai chữ số có dạng: \(\overline{ab}\)
Viết thêm chữ số 0 vào giữa hai chữ số của số đó ta được số mới là: \(\overline{a0b}\)
Theo bài ra ta có:
\(\overline{a0b}\) = 6 x \(\overline{ab}\)
100a + b = 60a + b
100a + b - 60a - 6b = 0
(100a - 60a) - (6b - b) = 0
40a - 5b = 0
8a - b = 0
8a = b
b ≤ 9 ⇒ 8a ≤ 9 ⇒ a ≤ 9 : 8 ⇒ a < 2 ⇒ a = 0; 1
Vì a không thể bằng không nên a = 1, b = 8a = 8.1 = 8
Vậy số cần tìm là 18

\(\dfrac{4}{5}+\dfrac{5}{7}:x=\dfrac{1}{6}\\ \dfrac{5}{7}:x=\dfrac{1}{6}-\dfrac{4}{5}\\ \dfrac{5}{7}:x=-\dfrac{19}{30}\\ X=\dfrac{5}{7}:\left(-\dfrac{19}{30}\right)\\ X=-\dfrac{150}{133}\)

số tiền chiếc tivi được giảm giá là
24.000.000 x 8,5% = 2040000(đồng)
số tiền chiếc tivi vào tháng 10 là
24.000.000 - 2040 000 = 21960000 (đồng)
đáp số 21960000đồng

\(\dfrac{3n+4}{n-3}=\dfrac{3n-9+13}{n-3}=\dfrac{3\left(n-3\right)+13}{n-3}=3+\dfrac{13}{n-3}\)
Để phân số đã cho là số nguyên thì \(13⋮\left(n-3\right)\)
\(\Rightarrow n-3\inƯ\left(13\right)=\left\{-13;-1;1;13\right\}\)
\(\Rightarrow n\in\left\{-10;2;4;16\right\}\)

\(A=\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2026^2}\)
\(=\dfrac{1}{2^2}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{1013^2}\right)\)
\(=\dfrac{1}{4}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{1013^2}\right)\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{1013^2}< \dfrac{1}{1012\cdot1013}=\dfrac{1}{1012}-\dfrac{1}{1013}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{1013^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{1012}-\dfrac{1}{1013}\)
=>\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{1013^2}< 1-\dfrac{1}{1013}< 1\)
=>\(A=\dfrac{1}{4}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{1013^2}\right)< \dfrac{1}{4}\cdot1=\dfrac{1}{4}\)

Tỉ số giữa phần diện tích trồng hoa hồng và diện tích khu vườn là:
\(\dfrac{3}{4+3}=\dfrac{3}{7}\)
Tỉ số giữa phần diện tích trồng hoa cúc và diện tích khu vườn là:
\(\dfrac{3}{7}\cdot\dfrac{5}{6}=\dfrac{5}{14}\)
Diện tích trồng hoa đồng tiền chiếm:
\(1-\dfrac{3}{7}-\dfrac{5}{14}=\dfrac{4}{7}-\dfrac{5}{14}=\dfrac{3}{14}\)(khu vườn)
Diện tích khu vườn là:
\(90:\dfrac{3}{14}=90\cdot\dfrac{14}{3}=420\left(m^2\right)\)

Chúng ta cần tìm giá trị của biểu thức:
\(\frac{a^{2} + b^{2}}{a b}\)
khi \(a , b\) là các số nguyên dương sao cho \(a^{2} + b^{2}\) chia hết cho \(a b\), tức là biểu thức này phải là một số nguyên.
Bước 1: Viết lại biểu thức
\(\frac{a^{2} + b^{2}}{a b} = \frac{a^{2}}{a b} + \frac{b^{2}}{a b} = \frac{a}{b} + \frac{b}{a}\)
Ta đặt \(x = \frac{a}{b} + \frac{b}{a}\), trong đó \(x\) phải là một số nguyên.
Bước 2: Định nghĩa \(x\)
Ta biết rằng bất đẳng thức AM-GM cho ta:
\(\frac{a}{b} + \frac{b}{a} \geq 2\)
Do \(x\) là số nguyên dương, giá trị nhỏ nhất của \(x\) là 2.
Bước 3: Tìm các giá trị hợp lệ
Ta xét trường hợp nhỏ nhất:
\(\frac{a}{b} + \frac{b}{a} = 2\)
Điều kiện này chỉ xảy ra khi \(a = b\). Thay vào biểu thức:
\(\frac{a^{2} + a^{2}}{a^{2}} = \frac{2 a^{2}}{a^{2}} = 2\)
Kết luận:
Vì bài toán yêu cầu \(\frac{a^{2} + b^{2}}{a b}\) là một số nguyên, giá trị hợp lệ duy nhất là 2.
Vậy thương của phép chia luôn bằng 2.
\(\dfrac{1}{7}\) là phân số tối giản nên không thể rút gọn
\(\frac17\) đã là phân số tối giản rồi nên không rút gọn được nữa bạn nhé.