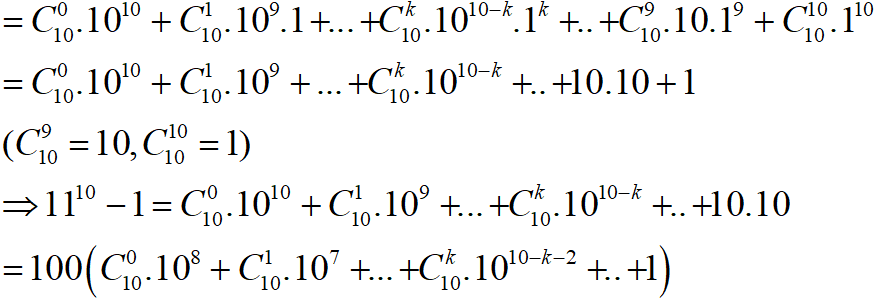\(\left|x-2\right|=\left|x^2-3x+2\right|\)

\(\Leftrightarrow\orbr{\begin{cases}x^2-3x+2=x-2\\x^2-3x+2=2-x\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x^2-4x+4=0\\x^2-2x=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}\left(x-2\right)^2=0\\x\left(x-2\right)=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)(thỏa).

\(\left|x-2\right|=\left|x^2-3x+2\right|\)

TH1 : \(x-2=x^2-3x+2\Leftrightarrow x^2-4x+4=0\Leftrightarrow\left(x-2\right)^2=0\Leftrightarrow x=2\)

TH2 : \(x-2=-x^2+3x-2\Leftrightarrow x^2-2x=0\Leftrightarrow x=0;x=2\)

Vậy tập nghiệm của pt là S = { 0 ; 2 } 

a, Ta có; \(11^{10}-1=\left(10+1\right)^{10}\) ( khai triển nhị thức Niu- tơn )

Do đó \(11^{10}-1\) chia hết cho 100

b, 

Đặt A=9.10n+18

27=9.3

Ta có:

A=9.\(10^n\)+18 = 9 ( \(10^n\) + 2 )

=> A ⋮ 9

Lại có:

 \(10^n+2\) = 10...0 + 2 = 10...02

=> A ⋮ 3 ⇒ A = 3k 

⇒ A=9.3 k=27k

=> A ⋮ 27

Vậy 9.10n+18⋮27 (Đpcm)

c,

Điều phải CM đúng với n = 1 , khi đó , ta có :

16¹ - 15.1 - 1 = 0 ⋮225

Gỉa sử điều phải CM đúng với : n = k , ta có :

16^k - 15.k - 1 ⋮225

Ta CMR điều phải CM cũng đúng với n = k + 1 , Ta có :

16^k+1 - 15( k + 1) - 1

= 16.16^k - 15k - 15 - 1 = ( 16^k - 15k - 1) + 15.16^k - 15

( Vì 16.16^k = ( 15 + 1)16^k = 16^k + 15.16^k )

Theo giả thiết trên thì : 16^k - 15^k - 1 ⋮ 225

Còn : 15.16^k - 15 = 15( 16^k - 1)

Mà : 16^k - 1 ⋮( 16 - 1)

⇒15( 16^k - 1) ⋮ 15.15 = 225

⇒ đpcm

A H B C 15 20 12 M N

a, Xét tam giác ABC và tam giác HBA ta có 

^B chung 

^BAC = ^BHA = 90⁰

Vậy tam giác ABC ~ tam giác HBA ( g.g )

b, Vì tam giác ABC ~ tam giác HBA ( cma )

\(\Rightarrow\frac{AB}{HB}=\frac{AC}{AH}\)( tỉ số đồng dạng )

\(\Rightarrow HB=\frac{AB.AH}{AC}=\frac{15.12}{20}=9\)cm 

c, Ta có : 

M là trung điểm BH => \(BM=MH=\frac{BH}{2}=\frac{9}{2}=4,5\)cm 

N là trung điểm AH => \(AN=NH=\frac{AH}{2}=\frac{12}{2}=6\)cm

Kết hợp với giả thiết ta có : \(AC.BM=AB.AN\Rightarrow20.4,5=15.6\)* đúng *

Vậy ta có đpcm