(2x⁴ - x³ + 3x²) : (-1/3 x²)

= 2x⁴ : (-1/3 x²) - x³ : (-1/3 x²) + 3x² : (-1/3 x²)

= -6x² + 3x - 9

  (2\(x^4\) - \(x^3\) + 3\(x^2\)) : (- \(\dfrac{1}{3}\)\(x^2\))

= \(x^2\).(2\(x^2\) - \(x\) + 3) : (\(x^2\)): (\(\dfrac{-1}{3}\))

= (2\(x^2\) - \(x\) + 3) x \(\dfrac{3}{-1}\)

= - 6\(x^2\) +3\(x\) - 9 

a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)

nên MAOB là tứ giác nội tiếp

b: Ta có; ΔOCD cân tại O

mà OK là đường trung tuyến

nên OK\(\perp\)CD tại K

Ta có: \(\widehat{OKM}=\widehat{OAM}=\widehat{OBM}=90^0\)

=>O,K,A,M,B cùng thuộc đường tròn đường kính OM

c: Xét (O) có

MA,MB là các tiếp tuyến

Do đó: MA=MB

=>M nằm trên đường trung trực của BA(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của BA(2)

Từ (1),(2) suy ra OM là đường trung trực của AB

=>OM\(\perp\)AB tại H

Xét ΔOHN vuông tại H và ΔOKM vuông tại K có

\(\widehat{HON}\) chung

Do đó: ΔOHN~ΔOKM

=>\(\dfrac{OH}{OK}=\dfrac{ON}{OM}\)

=>\(OH\cdot OM=OK\cdot ON\left(3\right)\)

Xét ΔOAM vuông tại A có AH là đường cao

nên \(OH\cdot OM=OA^2=R^2\left(4\right)\)

Từ (3),(4) suy ra \(OK\cdot ON=R^2=OD^2\)

=>\(\dfrac{OK}{OD}=\dfrac{OD}{ON}\)

Xét ΔOKD và ΔODN có

\(\dfrac{OK}{OD}=\dfrac{OD}{ON}\)

\(\widehat{KOD}\) chung

Do đó: ΔOKD~ΔODN

=>\(\widehat{OKD}=\widehat{ODN}=90^0\)

=>ND là tiếp tuyến của (O)

165 phút = \(\dfrac{165}{60}\) giờ  = 2\(\dfrac{3}{4}\) giờ

2,76 giờ

a) 30 m = 3000 cm

10 m = 1000 cm

Chiều dài trên bản vẽ:

3000 . 1/500 = 6 (cm)

Chiều rộng trên bản vẽ:

1000 . 1/500 = 2 (cm)

b) Diện tích khu đất trên bản vẽ:

6 . 2 = 12 (cm²)

Diện tích khu đất thực tế:

30 . 10 = 300 (m²)

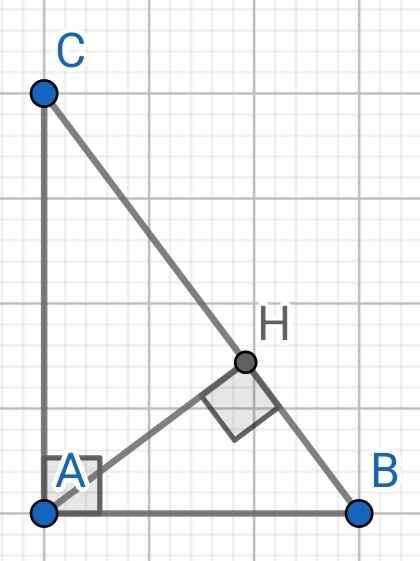
a) ∆ABC vuông tại A (gt)

⇒ BC² = AB² + AC² (Pythagore)

= 3² + 4²

= 25

⇒ BC = 5 (cm)

b) Xét hai tam giác vuông: ∆ABC và ∆HBA có:

∠A chung

⇒ ∆ABC ∽ ∆HBA (g-g)

⇒ AB/HB = BC/AB

⇒ HB = AB²/BC

= 3²/5

= 1,8 (cm)

⇒ HC = BC - HB

= 5 - 1,8

= 3,2 (cm)

c) Do ∆ABC ∽ ∆HBA (cmt)

⇒ AC/AH = BC/AB

⇒ AH = AB.AC/BC

= 3.4/5

= 2,4 (cm)