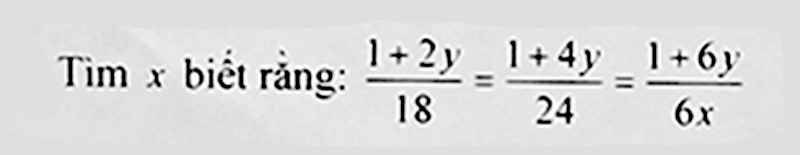
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔBAE vuông tại A và ΔBKE vuông tại K có
BE chung
\(\widehat{ABE}=\widehat{KBE}\)
Do đó: ΔBAE=ΔBKE
=>BA=BK
b: ΔBAE=ΔBKE
=>EA=EK
=>E nằm trên đường trung trực của AK(1)
Ta có: BA=BK
=>B nằm trên đường trung trực của AK(2)
Từ (1),(2) suy ra BE là đường trung trực của AK
=>BE\(\perp\)AK
c: Ta có: EA=EK
mà EK<EC(ΔEKC vuông tại K)
nên EA<EC
d: Xét ΔEAD vuông tại A và ΔEKC vuông tại K có
EA=EK
\(\widehat{AED}=\widehat{KEC}\)(hai góc đối đỉnh)
Do đó: ΔEAD=ΔEKC
=>AD=KC
Xét ΔBDC có \(\dfrac{BA}{AD}=\dfrac{BK}{KC}\)
nên AK//DC

Nó còn phải phụ thuộc vào hạnh kiểm nữa em nhé.

Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk$.
a.
$\frac{a}{a+b}=\frac{bk}{bk+b}=\frac{bk}{b(k+1)}=\frac{k}{k+1}$
$\frac{c}{c+d}=\frac{dk}{dk+d}=\frac{dk}{d(k+1)}=\frac{k}{k+1}$
$\Rightarrow \frac{a}{a+b}=\frac{c}{c+d}$
b.
$\frac{a-b}{c-d}=\frac{bk-b}{dk-d}=\frac{b(k-1)}{d(k-1)}=\frac{b}{d}$
$\frac{a+c}{b+d}=\frac{bk+dk}{b+d}=\frac{k(b+d)}{b+d}=k$
$\Rightarrow$ đề chưa đúng. Bạn xem lại.

Lời giải:
$3x=2y\Rightarrow \frac{x}{y}=\frac{2}{3}$
Khi đó:
$\frac{x}{yz}:\frac{y}{xz}=\frac{x.xz}{yz.y}=\frac{x^2}{y^2}=(\frac{x}{y})^2=(\frac{2}{3})^2=\frac{4}{9}$

Thời gian hai người đi từ đầu đến chỗ gặp là:
7h45p-7h15p=30p=0,5(giờ)
Tổng vận tốc của hai người là 15+4=19(km/h)
Độ dài quãng đường AB là:
19x0,5=9,5(km)

Nửa chu vi mảnh đất là 100:2=50(m)
Chiều dài mảnh đất là (50+10):2=60:2=30(m)
Chiều rộng mảnh đất là 30-10=20(m)
Diện tích mảnh đất là \(30\cdot20=600\left(m^2\right)\)
chiều dài Mđất là: (100+10): 2=55m
Chiều rọng Mđất là: 100-55=45m
S Mđất là: 55.45=2475 m vuông

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của CB
Xét ΔCBN có
CM là đường trung tuyến
\(CI=\dfrac{2}{3}CM\)
Do đó: I là trọng tâm của ΔCBN
Xét ΔCBN có
I là trọng tâm
H là trung điểm của BC
Do đó: I,N,H thẳng hàng

a: Xét ΔBAI vuông tại A và ΔBMI vuông tại M có
BI chung
\(\widehat{ABI}=\widehat{MBI}\)
Do đó: ΔBAI=ΔBMI
=>IA=IM
=>ΔIAM cân tại I
b: Xét ΔBNC có
NM,CA là các đường cao
NM cắt CA tại I
Do đó: I là trực tâm của ΔBNC
=>BI\(\perp\)NC
c: Sửa đề: Chứng minh AM//NC
Xét ΔBMN vuông tại M và ΔBAC vuông tại A có
BM=BA(ΔBMI=ΔBAI)
\(\widehat{MBN}\) chung
Do đó: ΔBMN=ΔBAC
=>BN=BC
Xét ΔBNC có \(\dfrac{BA}{BN}=\dfrac{BM}{BC}\)
nên AM//NC

\(\dfrac{6}{x}=\dfrac{10}{5}\)
=>\(x=6\cdot\dfrac{5}{10}\)
=>\(x=\dfrac{30}{10}=3\)


Tìm \(x\) biết: \(\dfrac{1+2y}{18}\) = \(\dfrac{1+4y}{24}\) = \(\dfrac{1+6y}{6x}\) (đk \(x\ne\) 0)
\(\dfrac{1+2y}{18}\) = \(\dfrac{1+4y}{24}\)
\(\dfrac{\left(1+2y\right).4}{72}\) = \(\dfrac{\left(1+4y\right).3}{72}\)
4 + 8y = 3 + 12y
4 + 8y - 3 - 12y = 0
(4 - 3) + (8y - 12y) = 0
1 - 4y = 0
4y = 1
y = \(\dfrac{1}{4}\)
Thay y = \(\dfrac{1}{2}\) vào biểu thức \(\dfrac{1+2.\dfrac{1}{4}}{18}\) = \(\dfrac{1+6.\dfrac{1}{4}}{6x}\)
\(\dfrac{1}{12}\) = \(\dfrac{5}{12x}\)
12\(x\) = 5.12
12\(x\) = 60
\(x\) = 60 : 12
\(x\) = 5
Vậy (\(x;y\)) = (5; \(\dfrac{1}{4}\))