cô vừ giao cho mình câu sau
Bạn An chọn ngẫu nhiêu 3 quả trong 1 hộp gồm 19 quả đánh số từ 1 đến 19 tỉnh sác suất để bạn An chọn ra 3 quả có tổng chia hết cho 4Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, để tính tổng A = 1 + 2 + 3 + 4 + … + 99 + 100, ta áp dụng công thức tổng của dãy số từ 1 đến n: S = (n * (n + 1)) / 2.
Với n = 100, ta có: A = (100 * (100 + 1)) / 2 = 5050.
b, để tính tổng B = 4 + 7 + 10 + 13 + … + 301, ta nhận thấy các số trong dãy này tạo thành một cấp số cộng với công sai d = 3.
Ta có công thức tổng của cấp số cộng: S = (n/2) * (a + l), trong đó n là số phần tử, a là số đầu tiên, l là số cuối cùng.
Số đầu tiên a = 4, số cuối cùng l = 301, và công sai d = 3.
Số phần tử n = ((l - a) / d) + 1 = ((301 - 4) / 3) + 1 = 100.
Vậy tổng B = (100/2) * (4 + 301) = 50 * 305 = 15250.
B2, để tính tổng của tất cả các số tự nhiên x, biết x là số có 2 chữ số và 12 < x < 91, ta cần tính tổng các số từ 13 đến 90.
Áp dụng công thức tổng của dãy số từ a đến b: S = ((b - a + 1) * (a + b)) / 2.
Với a = 13 và b = 90, ta có: S = ((90 - 13 + 1) * (13 + 90)) / 2 = (78 * 103) / 2 = 4014.
B3, để tính tổng của tất cả các số tự nhiên a, biết a có 3 chữ số và 119 < a < 501, ta cần tính tổng các số từ 120 đến 500.
Áp dụng công thức tổng của dãy số từ a đến b: S = ((b - a + 1) * (a + b)) / 2.
Với a = 120 và b = 500, ta có: S = ((500 - 120 + 1) * (120 + 500)) / 2 = (381 * 620) / 2 = 118260.

Số tiền còn lại sau khi ủng hộ quỹ: 1,570,000 - 500,000 = 1,070,000 đồng
Số tiền mẹ bù thêm: 712,000 đồng
Số tiền Tùng Lâm đã mua đôi giày: 1,070,000 + 712,000 = 1,782,000 đồng
Vậy đôi giày của Tùng Lâm đã mua với số tiền là 1,782,000 đồng.

4 - \(\dfrac{2}{5}\) = \(\dfrac{20}{5}\) - \(\dfrac{2}{5}\) = \(\dfrac{18}{5}\)
\(\dfrac{15}{4}\) - 2 = \(\dfrac{15}{4}\) - \(\dfrac{8}{4}\) = \(\dfrac{7}{4}\)
\(\dfrac{23}{6}\) - 3 = \(\dfrac{23}{6}\) - \(\dfrac{18}{6}\) = \(\dfrac{5}{6}\)

\(a.2^{x+2}-2^x=96\\ 2^x\cdot4-2^x=96\\ 2^x\cdot\left(4-1\right)=96\\ 2^x\cdot3=96\\ 2^x=96:3\\ 2^x=32\\ 2^x=2^5\\ =>x=5\)
\(2^{x+1}\cdot3^y=12^x\\ 2^{x+1}\cdot3^y=3^x\cdot2^{2x}\\ \left\{{}\begin{matrix}2^{x+1}=2^{2x}\\3^y=3^x\end{matrix}\right.\\ \left\{{}\begin{matrix}x+1=2x\\y=x\end{matrix}\right.\\ \left\{{}\begin{matrix}x=1\\y=x=1\end{matrix}\right.\\ \left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
\(c.10^x:5^y=20^y\\ 10^x:5^y=5^y\cdot4^y\\ 10^x=10^{2y}\\ =>x=2y\)

Lời giải:
Các cặp nguyên tố sinh đôi: $(3,5), (5,7), (11,13), (17,19)$

(x-1)(x-3)(x-4)>0
Trường hợp 1 :
x-1>0; x-3>0; x-4>0
Nên x>1; x>3; x>4
Vậy x>4 (hay x∈ Z/x ∈ { 5;6;7...})
Trường hợp 2 :
x-1>0; x-3<0; x-4<0
Nên x>1; x<3; x<4
Vậy 1<x<3 (hay x∈ Z/x ∈ { 2 })

\(xy-3x+y=20\)
\(\Rightarrow y\left(x+1\right)-3x=20\)
\(\Rightarrow y\left(x+1\right)-3x-3=20-3\)
\(\Rightarrow y\left(x+1\right)-3\left(x+1\right)=17\)
\(\Rightarrow\left(x+1\right)\left(y-3\right)=17\)
Vậy: \(x+1\) và \(y-3\) thuộc ước của 17
Mà \(Ư\left(17\right)=\left\{17;-17;1;-1\right\}\)
(Đến đây bạn lập bản ra nhé !)

a) \(\left(x-1\right)\left(x+2\right)\left(-x-3\right)=0\\ =>\left[{}\begin{matrix}x-1=0\\x+2=0\\-x-3=0\end{matrix}\right.\\ =>\left[{}\begin{matrix}x=1\\x=-2\\x=-3\end{matrix}\right.\)
b) \(xy-5y+5x-24=12\\ =>y\left(x-5\right)+5\left(x-5\right)+1=12\\ =>\left(y+5\right)\left(x-5\right)=11\)
Bổ sung đề : Tìm x,y nguyên
Vì x,y nguyên => x-5,y+5 nguyên
Mà : 11=1.11=(-1).(-11)
Đến đây bạn lập bảng giá trị rồi kết luận.

Ta có vì số dư luôn nhỏ hơn số chia nên số dư lớn nhất sẽ nhỏ hơn số chia 1 đv = 25 - 1 = 24
Ta có : số tự nhiên đó là 25 x 12 + 24 = 324
Kết luận : ...
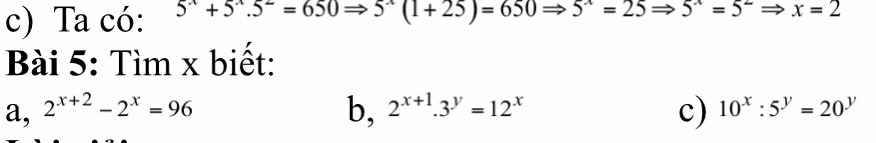
Số phần tử của không gian mẫu \(\left|\Omega\right|=C^3_{19}\)
Gọi A là biến cố: "An chọn ra 3 quả cho tổng chia hết cho 4."
Trong các số từ 1 đến 19 sẽ có 4 số chia hết cho 4; 5 số chia 4 dư 1; 5 số chia 4 dư 2 và 5 số chia 4 dư 3. Để tổng các số trên 3 quả chia hết cho 4 thì số dư của bộ số đó khi chia cho 4 (ta gọi là \(\left(a,b,c\right)\)) phải bằng 1 trong các bộ số sau:
\(\left(0,0,0\right)\), \(\left(0,1,3\right),\left(0,2,2\right),\left(1,1,2\right),\left(3,3,2\right)\).
Với TH \(\left(a,b,c\right)\rightarrow\left(0,0,0\right)\) thì có tất cả \(C^3_4=4\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(0,1,3\right)\) thì có tất cả \(4.5^2=100\) cách chọn
Với TH \(\left(a,b,c\right)\rightarrow\left(0,2,2\right)\) thì có tất cả \(4.C^2_5=40\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(1,1,2\right)\) thì có tất cả \(C^2_5.5=50\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(3,3,2\right)\) thì có tất cả \(C^2_5.5=50\) cách chọn.
Vậy \(\left|A\right|=4+100+40+50+50=244\).
\(\Rightarrow P\left(A\right)=\dfrac{\left|A\right|}{\left|\Omega\right|}=\dfrac{244}{C^3_{19}}=\dfrac{244}{969}\).
Vậy xác suất để An chọn ra 3 quả có tổng chia hết cho 4 là \(\dfrac{244}{969}\)