Cho góc bẹt xOy có tia phân giác Ot . Trên tia Ot lấy 2 điểm A ,B (A nằm giữa O và B ) . Lấy điểm C thuộc Ox sao cho OC=OB , lấy điểm D thuộc Oy sao cho OD=OA
a) chứng minh AC=BD và AC vuông góc với BD
b) gọi M .N lần lượt là trung điểm của AC và BD . chứng minh ON =OM
c) tính các góc của tam giác MON
d) chứng minh AD vuông góc với BC
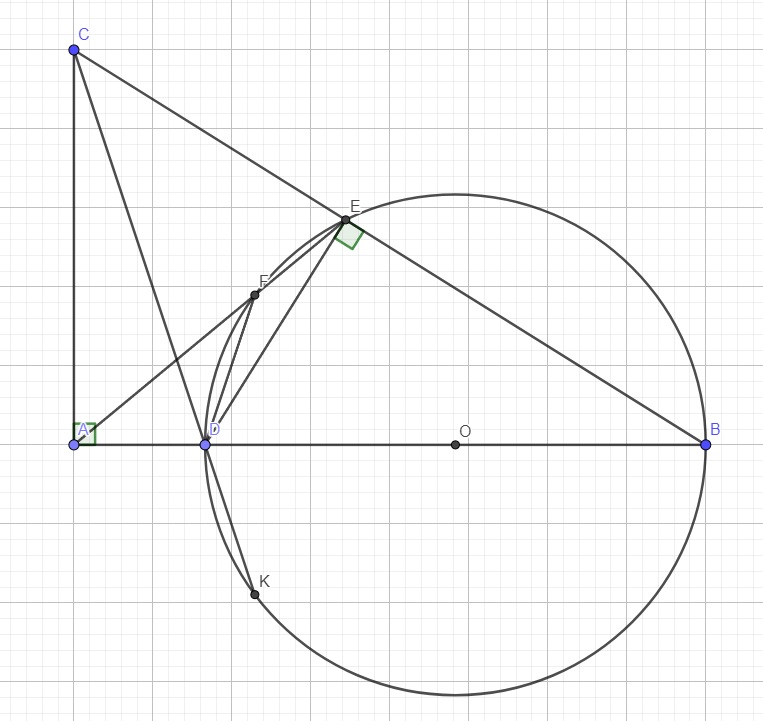
2) cho tam giác ABC có 3 góc nhọn . Vẽ AH vuông góc với AB tại I, vẽ HK vuông góc với AC tại K .Lấy E,F sao cho I là trung điểm của HE ,K là trung điểm của HF ,EF cắt AB ,AC lần lượt tại M,N
a) chứng minh MH =ME và chu vi tam giác MHN bằng EF
b) chứng minh AE =AF
c) nếu biết góc BAC =60 độ , Khi đó hãy tính các góc của tam giác AEF



Bài 1:
a: Ta có: Ot là phân giác của góc xOy
=>\(\widehat{xOt}=\widehat{yOt}=\dfrac{180^0}{2}=90^0\)
=>BO\(\perp\)DC
Xét ΔOAC vuông tại A và ΔODB vuông tại D có
OA=OD
OC=OB
Do đó: ΔOAC=ΔODB
=>AC=DB(1)
Ta có: ΔOAC=ΔODB
=>\(\widehat{OAC}=\widehat{ODB}\)
mà \(\widehat{OAC}+\widehat{OCA}=90^0\)
nên \(\widehat{ODB}+\widehat{OCA}=90^0\)
=>CA\(\perp\)BD
b: Ta có;ΔOAC vuông tại O
mà OM là đường trung tuyến
nên \(OM=\dfrac{AC}{2}\)(3)
=>OM=MA=MC
Ta có: ΔOBD vuông tại O
mà ON là đường trung tuyến
nên \(ON=\dfrac{BD}{2}\)(2)
=>ON=NB=ND
Từ (1),(2),(3) suy ra OM=ON
c: NB=NO nên \(\widehat{NBO}=\widehat{NOB}\)
MA=MO
nên \(\widehat{MAO}=\widehat{MOA}\)
\(\widehat{NOM}=\widehat{NOA}+\widehat{MOA}\)
\(=\widehat{NBO}+\widehat{MAO}=\widehat{DBO}+\widehat{CAO}\)
\(=\widehat{DBO}+\widehat{ODB}=90^0\)
=>ΔNOM vuông cân tại O
=>\(\widehat{ONM}=\widehat{OMN}=45^0\)
d: Xét ΔBDC có
CA,BO là các đường cao
CA cắt BO tại A
Do đó: A là trực tâm của ΔBDC
=>DA\(\perp\)BC