Ta có:

a³-b³=(a-b)³+3ab(a-b)

      Tại a-b=1 và ab=6 ta có:

a³-b³=1+18

         =19

     Vậy tại a-b=1 và ab=6 thì a³-b³=19  

\(\left(a-b\right)\left(a^2+ab+b^2\right)\)

\(a^2+ab+b^2\)

\(a^2-2ab+b^2+3ab\)

\(\left(a-b\right)^2+3.6\)

\(1+18=19\)

\(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=\left(x+y\right)^2-3xy=1+3=4\)

\(Q=2\left(x+y\right)\left(x^2-xy+y^2\right)-3\left(x^2+y^2\right)=-\left(x+y\right)^2=-1\)

 x^3 +y^3

=(x+y)^3

=1

Q=2(x^3 +y^3 )-3(x^2 +y^2)

=2(x+y)^3-3(x+y)^2

Thay x+y=1 vào đa thức Q có:

=2.1-3.1

=-1

Do ABCD là hình thang cân nên AD = BC, AC = BC, ˆD=ˆCD^=C^

Xét hai tam giác ADC và BCD, ta có: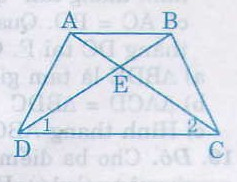

         AD = BC (gt)

         DC chung

Nên  ∆ADC =  ∆BCD (c.c.c)

Suy ra ˆC1=ˆD1C1^=D1^

Do đó tam giác ECD cân tại E, nên EC = ED

Ta lại có: AC = BD suy ra EA = EB

Chú ý: Ngoài cách chứng minh  ∆ADC =  ∆BCD (c.c.c) ta còn có thể chứng minh  ∆ADC =  ∆BCD (c.g.c) như sau:

AD = BC, ˆD=ˆCD^=C^ , DC là cạnh chung.

bn ơi trả lời sai đề

hok tốt

A= x(x-2)(x+2)-(x-3)(x^2 +3x+9)

=x^3+2x^2-2x^2-4x-x^3-3x^2-9x+3x^2+9x+27

=-4x+27

Thay x=1/4 vào đa thức A có:

-4.1/4+27

=-27

A=x(x-2)(x+2)-(x-3)(x²+3x+9) 

A=x(x²-4)-(x³+3x²+9x-3x²-9x-27)

A=x³-4x-x³+27

A=-4x+27

 Thay \(\frac{1}{4}\)vào biểu thức đã rút gọn, ta có :

   \(-4.\frac{1}{4}+27=-1+27=26\)

#H

A= x(x-2)(x+2)-(x-3)(x^2 +3x+9)

=x^3+2x^2-2x^2-4x-x^3-3x^2-9x+3x^2+9x+27

=-4x+27

Thay x=1/4 vào đa thức A có:

-4.1/4+27

=-27

\(A=x\left(x-2\right)\left(x+2\right)-\left(x-3\right)\left(x^2+3x+9\right)\)

\(A=x\left(x^2-4\right)-\left(x^3-27\right)=x^3-4x-x^3+27=27-4x\)

Thay \(x=\frac{1}{4}\) vào A ta có : \(A=27-4.\frac{1}{4}=27-1=26\)

VT=(a-1)(a-2)(1+a+a^2)(5+2a+a^2)

=(a^3−1)(a^3−8)

=a^6−8a^3−a^3+8

= a^6 -9a^3 +8=VP

⇒đpcm

có ai kb k

Trả lời:

Bn tham khỏa xem trong này nha:

https://h.vn/hoi-dap/question/384525.html

Nhớ t i c k nha

~HT~

\(\left(m-n\right)\left(m^2+mn+n^2\right)-\left(m+n\right)\left(m^2-mn+n^2\right)\)

\(=m^3-n^3-m^3-n^3\)

\(=-2n^3\)

Phương trình đã cho tương đương : m³ - n³ - ( m³ + n³ )

Tương đương vưới : m³ - n³ - m³ - n³ = 2n³ = 0