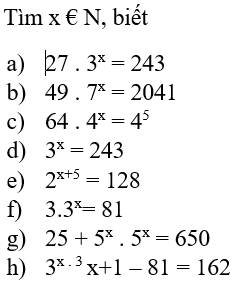
giúp tớ vs, tớ cần gấp loắm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, 3\(^x\).3 = 243
3\(^x\) = 243: 3
3\(^x\) = 81
3\(^x\) = 34
\(x\) = 4
b, \(x^{20}\) = \(x\)
\(x^{20}\) - \(x\) = 0
\(x\)(\(x^{19}\) - 1) = 0
\(\left[{}\begin{matrix}x=0\\x^{19}=1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
vậy \(\in\) {0; 1}
c, 2\(^x\).162 = 1024
2\(^x\) = 1024: 162
2\(^x\) = 210: 28
2\(^x\) = 22
\(x\) = 2
d, 64.4\(^x\) = 168
4\(^x\) = 168:64
4\(^x\) = (42)8 : 43
4\(^x\) = 413
\(x\) = 13
e, 2\(^x\).4 = 128
2\(^x\) = 128:4
2\(^x\) = 32
2\(^x\) = 25
\(x\) = 5

Để tìm hai số nhà đó, ta cần xác định tất cả các số chính phương và số lập phương có 2 chữ số. Các số chính phương có 2 chữ số là: 16, 25, 36, 49, 64, 81. Các số lập phương có 2 chữ số là: 8, 27, 64. Sau khi kiểm tra, ta thấy số nhà của Việt có thể là 16 và số nhà của Nam có thể là 64.

Lời giải:
$3^{2x+2}=9^{x+3}$
$3^{2x+2}=(3^2)^{x+3}=3^{2(x+3)}=3^{2x+6}$
$\Rightarrow 2x+2=2x+6$
$\Rightarrow 2=6$ (vô lý)
Vậy không có x thỏa mãn đề.

b, \(\dfrac{3}{1\times2}\) + \(\dfrac{3}{2\times3}\)+ \(\dfrac{3}{3\times4}\)+ ...+ \(\dfrac{3}{99\times100}\)
= \(3\) \(\times\) ( \(\dfrac{1}{1\times2}\) + \(\dfrac{1}{2\times3}\) + \(\dfrac{1}{3\times4}\)+...+ \(\dfrac{1}{99\times100}\)
= 3 \(\times\)( \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) +...+ \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\))
= 3 \(\times\) ( 1 - \(\dfrac{1}{100}\))
= 3 \(\times\) \(\dfrac{99}{100}\)
= \(\dfrac{297}{100}\)
c, \(\dfrac{3}{1\times2\times2}\) + \(\dfrac{3}{2\times3\times2}\)+ \(\dfrac{3}{3\times4\times2}\)+...+ \(\dfrac{3}{99\times100\times2}\)
= \(\dfrac{3}{2}\) \(\times\)( \(\dfrac{1}{1\times2}\) + \(\dfrac{1}{2\times3}\)+ \(\dfrac{1}{3\times4}\) +...+ \(\dfrac{1}{99\times100}\))
= \(\dfrac{3}{2}\) \(\times\) ( \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\)+ ... + \(\dfrac{1}{99}\)- \(\dfrac{1}{100}\))
= \(\dfrac{3}{2}\) \(\times\) (\(\dfrac{1}{1}\) - \(\dfrac{1}{100}\))
= \(\dfrac{3}{2}\) \(\times\) \(\dfrac{99}{100}\)
= \(\dfrac{297}{200}\)

a, 21.52.17 = 2.25.17 = 50.17 = 850
b, 22 + 23 + 24 = 4 + 8 + 16 = 28
c, 25.3 + 24:8 + 50: 52
= 32.3 + 16:8 + 50:25
=96 + 2 + 2
= 100
d, 112 - 102 - 32
= 121 - 100 - 9
= 21 - 9
= 12
e, 13 + 23 + 33 + 43 + 53
= ( 1+ 2+3+4+5)2
= 152
= 225

\(x\) + \(\dfrac{1}{4}\) + \(x\) + \(\dfrac{3}{2}\) = \(x\) + \(\dfrac{2}{3}\) + \(x\) + 4
\(x\) + \(x\) - \(x\) - \(x\) = \(\dfrac{2}{3}\) + 4 - \(\dfrac{3}{2}\) - \(\dfrac{1}{4}\)
0 = \(\dfrac{35}{12}\) (vô lý)
vậy \(x\) \(\in\) \(\varnothing\)

a) \(B\left(16\right)=\left\{0;16;32;48;64;80;96\right\}\)
b) \(U\left(135\right)=\left\{1;3;5;9;15;27;45\right\}\)
c) \(B\left(17\right)=\left\{0;17;34;51;68;85\right\}\)
d) \(U\left(75\right)=\left\{1;3;5;15;25;75\right\}\)
e) \(B\left(33\right)=\left\{0;33;66\right\}\)
f) \(U\left(42\right)=\left\{1;2;3;6;7;14;21;42\right\}\)

\(a\times100\) + 50 + \(c\) = \(\overline{a5c}\)
\(a\times100\) + \(b\times10\) + 6 = \(\overline{ab6}\)
a, 27.\(3^x\) = 243
\(3^x\) = 243 : 27
\(3^x\) = 9
\(3^x\) = 32
\(x\) = 2
b, 49.7\(^x\) = 2041
7\(^x\) = 2041: 49
7\(^x\) = 41,65
\(x\) = log741,56
\(x\) ≈ 1,916
c, 64.4\(^x\) = 4\(^5\)
4\(^x\) = 45 : 64
4\(^x\) = 4
\(x\) = 1
d, 3\(^x\) = 243
3\(^x\) = 35
\(x\) = 5
e, 2\(^{x+5}\) = 128
\(2^{x+5}\) = 27
\(x+5\) = 7
\(x\) = 7 - 5
\(x\) = 2
f, 3.3\(^x\) = 81
3\(^x\) = 81 : 3
3\(^x\) = 27
3\(^x\) = 33
\(x\) = 3
g, 25 + 5\(^x\).5\(^x\) = 650
5\(^{2x}\) = 650 - 25
5\(^{2x}\) = 625
5\(^{2x}\) = 54
2\(x\) = 4
\(x\) = 2