có tồn tại 2 số dương a,b khác nhau để 1/a-1/b=1/a-b không ?Vì sao
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, (72 - 8 \(\times\)9): (20 + 21 + 23 + 24 + 25)
= (72 - 72): ( 20 + 21 + 23 + 24 + 25)
= 0: ( 20 + 21 + 23+ 24 + 25)
= 0
b, (50 \(\times\) 9 - 25 \(\times\) 18) \(\times\) ( 1 + 2 + 3 + ...+9)
= ( 450 - 450 )\(\times\) ( 1 + 2 + 3 +...+9)
= 0 \(\times\)( 1 + 2 + 3 +...+ 9)
= 0
c, ( 11 + 13 + 15 + ...+ 19) \(\times\) ( 6 \(\times\) 8 - 48)
= ( 11 + 13 + 15+...+ 19) \(\times\) ( 48 - 48)
= ( 11 + 13 + 15 + ...+ 19) \(\times\) 0
= 0

a, 17 \(\times\) 8 + 17 \(\times\) 2
= 17 \(\times\) ( 8 + 2)
= 17 \(\times\) 10
= 170
b, 12 \(\times\) 24 - 2 \(\times\) 24
= 24 \(\times\) ( 12 - 2)
= 24 \(\times\) 10
= 240
c, 54 \(\times\) 113 + 45 \(\times\)113 + 113
= 113 \(\times\) ( 54 + 45 + 1)
= 113 \(\times\) 100
= 11300
d, 54 \(\times\) 47 - 47 \(\times\) 53 - 20 - 27
= 54 \(\times\) 47 - 47 \(\times\) 53 - 47
= 47 \(\times\) ( 54 - 53 - 1)
= 47 \(\times\) 0
= 0
e, 10000 - 47 \(\times\) 72 - 47 \(\times\) 28
= 10000 - 47 \(\times\)( 72 + 28)
= 10000 - 47 \(\times\) 100
= 10000 - 4700
= 5300

a, 89 + 32 + 11 + 68
= (89 + 11) + (32 + 68)
= 100 + 100
= 200
b, 349 + 602 + 651 + 398
= (349 + 651) + (602 + 398)
= 1000 + 1000
= 2000
c, 115 + 122 - 55 + 18
= ( 115 - 55) + ( 122 + 18)
= 60 + 140
= 200
d, 3145 - 246 - 145 + 4246
= ( 3145 - 145) + ( 4246 - 246)
= 3000 + 4000
= 7000
e, 52 - 42 + 37 + 28 - 38 + 63
(52 - 42) - ( 38 - 28) + ( 37 + 63)
= 10 - 10 + 100
= 100
f, 1 + 3 + 5 + 7 + 13 + 15 + 17 + 19
= (1 + 19) + (3 + 17) + (5 + 15) + ( 7 + 13)
= 20 + 20 + 20 + 20
= 80


2x3,12x1,25x0,25x10=2x3,12x(1,25:0,25x10)
=2x3,12 x50
=100x3,12=312

12,48: 0,5 \(\times\) 6,25 \(\times\) 4 \(\times\) 2
= 12,48 \(\times\) 2 \(\times\) 2 \(\times\) (6,25 \(\times\) 4)
= 12,48 \(\times\)4 \(\times\) 25
= 12,48 \(\times\) 100
= 1248
12,48:0,5x6,25x4x2=24,96x6,25x4x2=24,96x(6,25x4x2)
=(24,96x100):2
=2496:2=1248

a) (-35,8) + (-17,2) + 16,4 + 4,6
= [ (-35,8) + (-17,2) ] + (16,4 + 4,6)
= -53 + 21
= -32
b) (5,3 - 2,8) - (4 + 5,3)
= 2,5 - 9,3
= -6,8
c) (34,72 + 32,28):5 - (57,25 - 36,05):2
= 67:5 - 21,2:2
= 13,4 - 10,6
= 2,8
d) 2,5.(-4,68) + 2,5.(-5,32)
= 2,5.[ (-4,68) + (-5,32) ]
= 2,5. (-10)
= -25
e) 5,36. 12,34 + (-5,36). 2,34
= 5,36. 12,34 - 5,36. 2,34
= 5,36. (12,34 - 2,34)
= 5,36. 10
= 53,6
a,-35,8+(-17,2)+16,4+4,6=(-35,8-17,2)+(16,4+4,6=-53+21=-32
b,(5,3-2,8)-(4+5,3)=5,3-2,8-4-5,3=(5,3-5,3)+(-2,8-4)=0-6,8=-6,8.
c,(34,72+32,28):5-(57,25-36,05):2=67:5-21,2:2=13.4-10.6=2,8
d,2,5(-4,68)+2,5(-5,32)=2,5(-4,68-5,32)=2,5x(-10)=-25
e,5,36x12,34+(-5,36)x2,34=5,36(12,34-2,34)=5,36x10=53,6
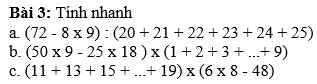


\(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{a-b}\)
\(\Rightarrow\dfrac{b\left(a-b\right)}{ab\left(a-b\right)}+\dfrac{a\left(a-b\right)}{ab\left(a-b\right)}=\dfrac{ab}{ab\left(a-b\right)}\left(a,b\ne0;a\ne b;a,b>0\right)\)
\(\Rightarrow\left(a-b\right)\left(b-a\right)=ab\)
\(\Rightarrow-\left(a-b\right)\left(a-b\right)=ab\)
\(\Rightarrow-\left(a-b\right)^2=ab\left(1\right)\)
mà \(\left\{{}\begin{matrix}-\left(a-b\right)^2< 0\\ab>0\end{matrix}\right.\)
\(\Rightarrow\left(1\right)\) vô lý
⇒ không có 2 số a≠b; a,b>0 thỏa đề bài