
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 22:
A={x\(\in N\)|0<x<=5}
Bài 21: C={x\(\in\)N|7<=x<=14}
Bài 20: B={\(x\in\)N|7<x<17}
Bài 19: A={x\(\in\)N|x>=8}
Bài 18:
C={x\(\in\)N|x>11}
bài 17:
B={\(x\in\)N|x<8}
Bài 16:
A={x\(\in\)N|x<3}

\(\dfrac{2^{17}\cdot9^4}{6^3\cdot8^3}\)
\(=\dfrac{2^{17}\cdot3^8}{2^3\cdot3^3\cdot2^9}\)
\(=\dfrac{2^{17}\cdot3^8}{2^{12}\cdot3^3}\)
\(=2^5\cdot3^5\)
\(=6^5=7776\)

a: A={1;2;3;4;5;6}; B={1;3;5;7;9}
=>C={2;4;6}
b: D={7;9}
c: E={1;3;5}

Ư(54)={1;-1;2;-2;3;-3;6;-6;9;-9;18;-18;27;-27;54;-54}
=>Các số vừa là bội của 3 vừa là ước của 54 là 3;-3;6;-6;9;-9;18;-18;27;-27;54;-54
Giải: 54 = 2.33
Ư(54) = {-54; -27; - 18; - 9; - 6; -3; - 2; -1; 1; 2; 3; 6; 9; 18; 27; 54}
Những số vừa là ước của 54 vừa là bội của 3 là các số thuộc tập B trong đó:
B = {- 54; - 27; - 18; - 9; - 6; - 3; 3; 6; 9; 18; 27; 54}

Liệt kê theo cặp các ước của 180.
Ư(180) = {1; 180; 2; 90; 3; 60; 4; 45; 5; 36; 6; 30; 9; 20; 10; 18; 15; 12}
P là tập hợp các ước không nguyên tố của 180.
suy ra, P = {1; 180; 90; 60; 4; 45; 36; 6; 30; 9; 20; 10; 18; 15; 12}.
Vậy tập hợp P có 15 phần tử.
Vậy số phần tử của tập hợp P là: 15 phần tử
180 = 22.32.5
Số ước số của 180 là: (2 + 1).(2 + 1).(1 + 1) = 18 (ước)
Số ước số là số nguyên tố của 180 là 3 ước đó là các ước 2; 3; 5
Số ước số không phải là số nguyên tố của 180 là: 18 - 3 = 15 (ước)
Kết luận P có 15 phần tử

\(\text{có phải bạn muốn là như này ko?}\)
\(\dfrac{45^{10}\times5^{10}}{75^{10}}\)
\(\text{Ta tách }\)\(45^{10}\) \(và\) \(75^{10}\)
\(45^{10}=\left(5\times3\times3\right)^{10}=5^{10}\times3^{10}\times3^{10}\) \(75^{10}=\left(5\times5\times3\right)^{10}=5^{10}\times5^{10}\times3^{10}\)
\(\text{Ta có:}\)
\(\dfrac{5^{10}\times3^{10}\times3^{10}\times5^{10}}{5^{10}\times5^{10}\times3^{10}}\)
\(=\) \(\dfrac{5^{20}\times3^{10}\times3^{10}}{5^{20}\times3^{10}}\)
\(=\) \(\dfrac{3^{20}}{3^{10}}\)
\(=\)\(3^{10}\)
\(\text{~Hok tốt~}\)
\(\text{@3a3sontung}\)

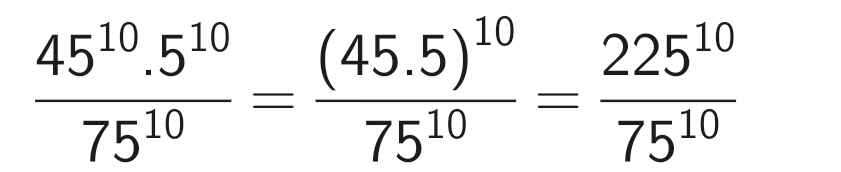
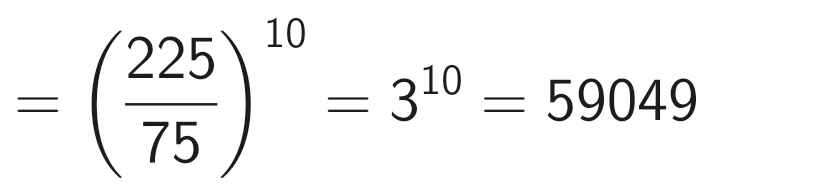
Bài 1 :
\(i,25.\left(x-4\right)=0\)
\(x-4=0:25\)
\(x-4=0\)
\(x=0+4\)
\(x=4\)
Vậy .....
\(m,34.\left(2x-6\right)=0\)
\(2x-6=0:34\)
\(2x-6=0\)
\(2x=0+6\)
\(2x=6\)
\(x=6:2\)
\(x=3\)
Vậy ....
\(n,2023.\left(3x-12\right)=0\)
\(3x-12=0:2023\)
\(3x-12=0\)
\(3x=0+12\)
\(3x=12\)
\(x=12:3\)
\(x=4\)
Vậy...
\(o,47.\left(5x-15\right)=0\)
\(5x-15=0:47\)
\(5x-15=0\)
\(5x=0+15\)
\(5x=15\)
\(x=15:5\)
\(x=3\)
Vậy....
\(p,13.\left(4x-24\right)=0\)
\(4x-24=0:13\)
\(4x-24=0\)
\(4x=0+24\)
\(4x=24\)
\(x=24:4\)
\(x=6\)
Vậy...
\(s,2.\left(x-5\right)-17=25\)
\(2.\left(x-5\right)=25+17\)
\(2.\left(x-5\right)=42\)
\(x-5=42:2\)
\(x-5=21\)
\(x=21+5\)
\(x=26\)
Vậy...
\(t,3.\left(x+7\right)-15=27\)
\(3.\left(x+7\right)=27+15\)
\(3.\left(x+7\right)=42\)
\(x+7=42:3\)
\(x+7=14\)
\(x=14-7\)
\(x=7\)
Vậy...
\(u,15+4.\left(x-2\right)=95\)
\(4.\left(x-2\right)=95-15\)
\(4.\left(x-2\right)=80\)
\(x-2=80:4\)
\(x-2=20\)
\(x=20+2\)
\(x=22\)
Vậy...
\(w,24+3.\left(5-x\right)=27\)
\(3.\left(5-x\right)=27-24\)
\(3.\left(x-5\right)=3\)
\(x-5=3:3\)
\(x-5=1\)
\(x=1+5\)
\(x=6\)
Vậy...
Bài 2 :
\(a,\left(x-2021\right).958=0\)
\(x-2021=0:958\)
\(x-2021=0\)
\(x=0+2021\)
\(x=2021\)
Vậy...
\(b,959.\left(x-7\right)=0\)
\(x-7=0:959\)
\(x-7=0\)
\(x=0+7\)
\(x=7\)
Vậy....
\(e,45.\left(91-x\right)=90\)
\(91-x=90:45\)
\(91-x=2\)
\(x=91-2\)
\(x=89\)
Vậy...
\(g,5x+73.21=73.26\)
\(5x+1533=1898\)
\(5x=1898-1533\)
\(5x=365\)
\(x=365:5\)
\(x=73\)
Vậy...
\(h,\left(x-12\right).105=525\)
\(x-12=525:105\)
\(x-12=5\)
\(x=5+12\)
\(x=17\)
Vậy...
\(i,47.\left(27-x\right)=47\)
\(27-x=47:47\)
\(27-x=1\)
\(x=27-1\)
\(x=26\)
Vậy ...
\(j,2x+69.2=69.4\)
\(2x+138=276\)
\(2x=276-138\)
\(2x=138\)
\(x=138:2\)
\(x=69\)
Vậy ...
\(l,\left(x-40\right).15=15.3\)
\(\left(x-40\right).15=45\)
\(x-40=45:15\)
\(x-40=3\)
\(x=3+40\)
\(x=43\)
Vậy...