
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


S A B C D E F I K M
a/
Trong mp(SAC) Gọi K là giao của EF và AC
\(K\in EF\)
\(K\in AC;AC\in\left(ABC\right)\Rightarrow K\in\left(ABC\right)\)
=> K là giao của EF với (ABC)
b/
Trong mp (SBC), Gọi M là giao của SI với BF
\(M\in SI;SI\in\left(SAI\right)\Rightarrow M\in\left(SAI\right)\)
\(M\in BF;BF\in\left(ABF\right)\Rightarrow M\in\left(ABF\right)\)
\(A\in\left(SAI\right);A\in\left(ABF\right)\)
=> AM là giao tuyến giữa (SAI) và (ABF)
c/
\(I\in\left(SAI\right)\)
\(I\in BC;BC\in\left(BCE\right)\Rightarrow I\in\left(BCE\right)\)
\(E\in SA;SA\in\left(SAI\right)\Rightarrow E\in\left(SAI\right)\)
\(E\in\left(BCE\right)\)
=> IE là giao tuyến giữa (SAI) và (BCE)

a; (135 - 35).(-37) + 37.(- 42 - 58)
= 100.(-37) + 37.(-100)
= - 100.(37+ 37)
= -100. 74
= - 7400
b; - 65.(87 - 17) - 87.(17 - 65)
= - 65.87 + 65.17 - 87.17 + 87.65
= (-65.87 + 87.65) - (87.17 - 65.17)
= 0 + 17.(87- 65)
= 17.(-22)
= - 374
c; [3.(-2) - (-8)]. (-7 - (-2).(-5))
= [-6 + 8].(-7 - 10)
= 2.(-17)
= - 34
d; 39.(-12) + (-39) + (117).29
= - 39.(12 + 1) + 3393
= -39.13 + 3393
= - 507 + 3393
= 2886
e; 63.(-71 - 55) - 71.(-55 - 63)
= -63.71 - 63.55 + 71.55 + 71.63
= (63.71 - 63.71) + (71.55 - 63.55)
= 0 + 55.(71 - 63)
= 55.8
= 440

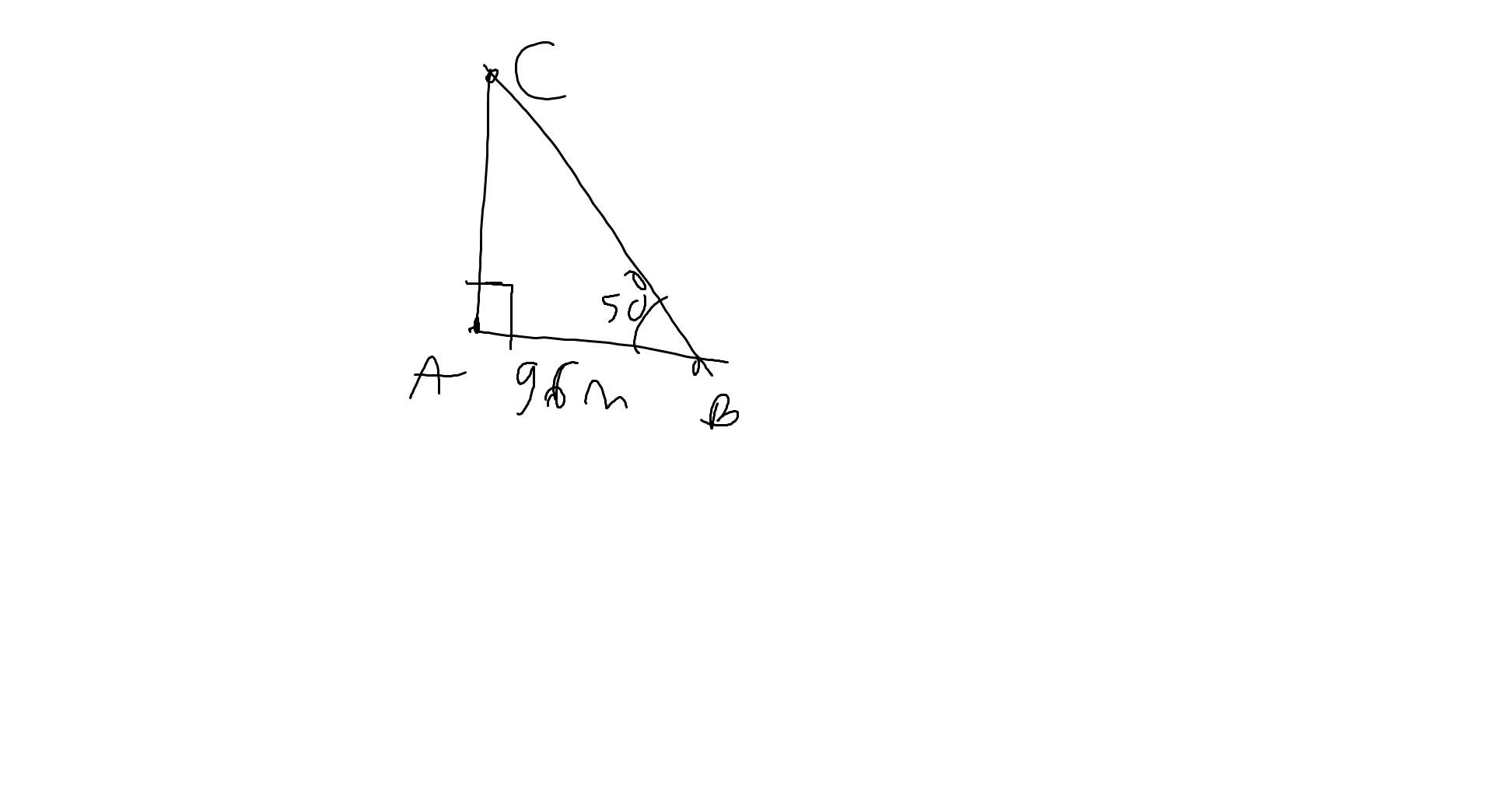
Gọi AB là bóng của cây trên mặt đất, AC là chiều cao của cây
Theo đề, ta có: AB\(\perp\)AC tại A, AB=96m; \(\widehat{B}=50^0\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(AC=AB\cdot tanB=96\cdot tan50\simeq114,4\left(m\right)\)

mik thì 11/11 mí thi mik nghĩ bn phải chăm chỉ ôn luyện thôi dạng chính là rơi vào ước chung,ước,ước chung lớn nhất và bội,bội chung ,bội chung nhỏ nhất đó là đối với những bài toán đố thôi à mik chỉ biết vậy à
CHÚC BN THI TOT NGHE

S = 5 + 52 + 53 + 54 +...+ 52019
S= (5 + 52 + 53) +(54 + 55 + 56)+...+(52017+52018+52019)
S=5(1 + 5+ 25 )+ 54 (1 + 5 + 25) +...+52017(1 + 5 + 25)
S = 5. 31 + 54 + 31 +...+ 52017 .31
S= 31 ( 5 + 54 +...+52017 )
⇒ S ⋮ 31 ( Do có thừa số 31)
S = 5 + 52 + 53 + 54 +..+ 52019
S = 51 + 52 + 53 + 54 + ... + 52019
Xét dãy số: 1; 2; 3; 4;...;2019; dãy số này là dãy số cách đều khoảng cách là: 2 - 1 = 1
Số số hạng là: (2019 - 1) : 2019 (số hạng)
Vì 2019 : 3 = 673 nên nhóm ba số hạng liên tiếp của A thành một nhóm ta được:
A = (5 + 52 + 53) + (54 + 55 + 56) + ... + (52017+ 52018 + 52019)
A = 5(1 + 5 + 52) + 54.(1 + 5 + 52) + ... + 52017.(1 + 5+ 52)
A = (1 + 5 + 52).(5 + 54 + .. + 52017)
A = (1 + 5 + 25).(5 + 54 + ... + 52017)
A = 31.(5 + 54 + ...+ 52017) ⋮ 31 (đpcm)

a: Xét ΔOAB có OA=OB=AB
nên ΔOAB đều
=>\(\widehat{OBA}=\widehat{OAB}=\widehat{AOB}=60^0\)
Xét ΔBCO có BC=BO
nên ΔBCO cân tại B
Xét ΔBCO có \(\widehat{ABO}\) là góc ngoài tại B
nên \(\widehat{ABO}=\widehat{BOC}+\widehat{BCO}\)
=>\(2\cdot\widehat{ACD}=60^0\)
=>\(\widehat{ACD}=\dfrac{60^0}{2}=30^0\)
b: Xét ΔOAC có
OB là đường trung tuyến
\(OB=\dfrac{AC}{2}\)
Do đó: ΔOAC vuông tại O
BA=BC
mà BA=3cm
nên BC=3cm
AC=3+3=6(cm)
ΔOAC vuông tại O
=>\(OA^2+OC^2=AC^2\)
=>\(OC=\sqrt{6^2-3^2}=3\sqrt{3}\left(cm\right)\)
OD+DC=OC
=>\(DC=OC-OD=3\sqrt{3}-3\left(cm\right)\)

\(n-2000=a^2\left(a\in N\right)\Rightarrow n=a^2+2000\left(1\right)\)
\(n-2011=b^2\left(b\in N\right)\Rightarrow n=b^2+2011\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow a^2+2000=b^2+2011\)
\(\Rightarrow a^2-b^2=11\)
\(\Rightarrow\left(a-b\right)\left(a+b\right)=11\)
\(\Rightarrow\left(a-b\right);\left(a+b\right)\in U\left(11\right)=\left\{1;11\right\}\)
\(\Rightarrow\left(a;b\right)=\left\{6;5\right\}\)
\(\left(1\right)\Rightarrow n=36+2000=2036\)
Kiểm tra \(\left(2\right)\Rightarrow n=25+2011=2036\left(đúng\right)\)
Vậy \(n=2036\)
Đây là toán nâng cao chuyên đề giải phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Vì n - 2000 là số chính phương nên n - 2000 = k2 (k \(\in\) N)
Vì n - 2011 là số chính phương nên n - 2011 = d2(d\(\in\) N); d < k
Hiệu của hai số trên là: n - 2000 - (n - 2011) = k2 - d2
n - 2000 - n + 2011 = k2 - d2
(n - n) + (2011 - 2000) = k2 - d2
0 + 11 = k2 - kd + kd - d2
11 = (k2 - kd) + (kd - d2)
11 = k(k - d) + d(k - d)
11 = (k - d).(k + d); Ư(11) = {1; 11}
Vì k; d \(\in\) N ta có: k - d < k + d ⇒ k - d = 1; k + d = 11
k - d = 1 ⇒ k = 1 + d ⇒ 1 + d + d = 11 ⇒ d + d = 11 - 1
⇒ 2d = 10 ⇒ d = 10 : 2 = 5 ⇒ n - 2011 = d2 = 52 = 25
⇒ n = 2011 + 25 = 2036
Vậy n = 2036

C = 1 + 2 + 22 + ... + 22008
C = 20 + 21 + 22 + ... + 22008
Xét dãy số: 0; 1; 2;...; 2008
Dãy số trên là dãy số cách đều với khoảng cách là: 1 - 0 = 1
Dãy số trên có số số hạng là: (2008 - 0) : 1 + 1 = 2009
Vì 2009 : 3 = 669 dư 2 nên nhóm ba số hạng liên tiếp của C vào nhau ta được:
C = 1+2 + (22 + 23 + 24) + (25 + 26 + 27) + .. +(22006+ 22007 + 22008)
C = 3 + 22.(1 + 2+ 22) + 25.(1 + 2 + 22) + .. + 22006.(1 + 2 + 22)
C = 3 + (1 + 2+ 22).(22 + 25 + ... + 22006)
C = 3 + 7.(22 + 25 + ... + 22006)
7.(22 + 25 + ... + 22006) ⋮ 7; 3 : 7 dư 3 vậy
C = 1 + 2 + 22 + ...+ 22008 chia 7 dư 3. (đpcm)

a: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//EB
b: Xét ΔMAI và ΔMEK có
MA=ME
\(\widehat{MAI}=\widehat{MEK}\)(cmt)
AI=EK
Do đó: ΔMAI=ΔMEK
=>\(\widehat{AMI}=\widehat{EMK}\)
=>\(\widehat{EMK}+\widehat{EMI}=180^0\)
=>I,M,K thẳng hàng