một bể nước hình hộp chữ nhật có chiều dài là 50cm chiều rộng 20 cm chiều cao 40cm a tính thể tích b giả sử lúc đầu bể bể nước đầy hỏi lấy đi 3600 cm3 nước thì mực nước trong bể là bnh cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


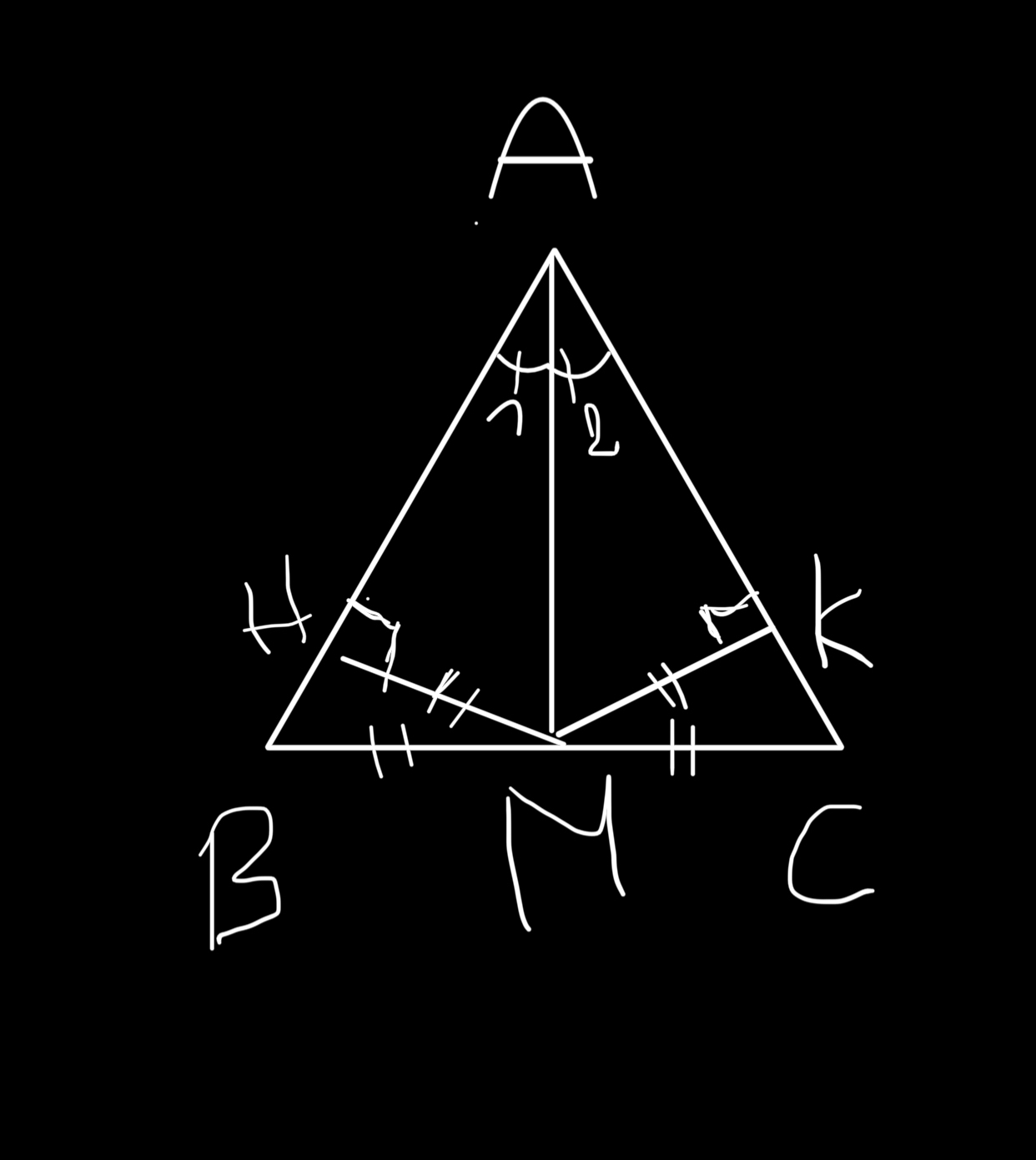
Ký hiệu vậy chưa được em. Vì em ký hiệu vậy nghĩa là BM = CM = HM = KM
Trong khi chỉ có BM = CM; HM = KM

5x/7 = 10/-3
=> 5x.(-3) = 7.10
5x.(-3) = 70
5x = 70/-3
x = -70/3 : 5
x = -14/3
Vậy x = -14/3
#ngophuongloan(chipcuti)
Chúc bạn học tốt hjhj!!
Vì \(\frac{5x}{7}=\frac{10}{-3}\) là một tỉ lệ thức
\(\Rightarrow5x.\left(-3\right)=7.10\)
\(5x.\left(-3\right)=70\)
\(5x=70:\left(-3\right)\)
\(5x=\frac{-70}{3}\)
\(x=\left(-\frac{70}{3}\right):5\)
\(x=-\frac{14}{13}\)
Vậy \(x=-\frac{14}{13}\)

Diện tích mảnh vườn hình chữ nhật là : 35 . 28 = 980 (\(m^2\))
Số ki-lô-gam cà chua thu hoạch được trên cả mảnh vườn là :
980 : 4 . 3 = 735 (kg)
Đ/s : 735 kg
giải
Diện tích mảnh vườn hình chữ nhật là:
35 . 28 =980 (m2)
Tổng số kg cà chua thu hoạch được trên mảnh vườn là:
980:4= 254 (kg)
sai cho tớ xl ạ

\(\dfrac{x}{4}=\dfrac{x\cdot2}{4\cdot2}=\dfrac{2x}{8}\)
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{2x}{8}=\dfrac{y}{5}=\dfrac{2x-y}{8-5}=\dfrac{12}{3}=4\\ \dfrac{2x}{8}=4\Rightarrow x=16\\ \dfrac{y}{5}=4\Rightarrow y=20\)
vậy x = 16; y = 20
có x/4=y/5 suy ra 2x/8= y/5
áp dụng t/c của dãy tỉ số bằng nhau ta có
2x/8=y/5=2x-y/8-5=4
suy ra
2x/8=4 y/5=4
x=16 y=20

Giải:
Gọi số vở của ba lớp 7A; 7B; 7C lần lượt là: \(x;y;z\) (\(x;y;z\in N\) *)
Theo bài ra ta có: \(\frac{x}{10}\) = \(\frac{y}{14}\) = \(\frac{z}{13}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{10}\) = \(\frac{y}{14}=\frac{z}{13}\) = \(\frac{z-x}{13-10}\) = \(\frac{30}{3}\) = 10
\(x\) = 10 x 10 = 100(quyển)
y = 10 x 14 = 140 (quyển)
z = 10 x 13 = 130 (quyển)
Kết luận số vở lớp 7A; 7B; 7C góp được lần lượt là:
100; 130; 140 quyển

Giải:
Theo bài ra ta có:
\(\frac{A}{3}=\frac{B}{5}=\frac{C}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{A}{3}=\frac{B}{5}=\frac{C}{7}\) = \(\frac{A+B+C}{3+5+7}\) = \(\frac{180}{15}\) = 12\(^0\)
A = 12\(^0\) x 3 = 36\(^0\)
B = 12\(^0\) x 5 = 60\(^0\)
C = 12\(^0\) x 7 = 84\(^0\)
Gọi ba góc $\widehat {A} ; \widehat {B} ; \widehat {C}` trong $\triangleABC$ lần lượt là $x;y;z (x;y;z \in N$$***$`)`
Theo đề bài , các góc $\widehat {A} ; \widehat {B} ; \widehat {C}$ tỉ lệ với các số `3,5,7`
$\Rightarrow$$\frac{x}{3} = \frac {y}{5} = \frac {z}{7}$
Trong một tam giác , tổng cả ba góc trong tam giác bằng $180^\circ$
$\Rightarrow$$x+y+z = 180^\circ$
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
$\frac{x}{3} = \frac {y}{5} = \frac {z}{7} = \frac {x+y+z}{3+5+7} = \frac {180^\circ}{15} = 12^\circ$
Khi đó :
$\frac {x}{3} = 12^\circ \Rightarrow x = 12^\circ . 3 = 36^\circ$
$\frac {y}{5} = 12^\circ \ Rightarrow y = 12^\circ . 5 = 60^\circ$
$\frac {z}{7} = 12^\circ \Rightarrow z = 12^\circ . 7 = 84^\circ$
Vậy số đo $\widehat {A} ; \widehat {B} ; \widehat {C}$ trong $\triangle ABC$ lần lượt là : $36^\circ ; 60^\circ ; 84^\circ$

Giải:
Theo bài ra ta có:
\(\frac{A}{3}=\frac{B}{5}=\frac{C}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{A}{3}=\frac{B}{5}=\frac{C}{7}\) = = \(\frac{A+B+C}{3+5+7}\) = \(\frac{180}{15}\) = 12\(^0\)
A = 12\(^0\) x 3 = 36\(^0\)
B = 12\(^0\) x 5 = 60\(^0\)
C = 12\(^0\) x 7 = 84\(^0\)
Thể tích của bể là:
50 x 20 x 40 = 40 000 ( cm3 )
Sau khi lấy đi 3600 cm3 thì thể tích nước còn lại trong bể là:
40 000 - 3 600 = 36 400 ( cm3 )
Mực nước trong bể sau khi lấy đi 3600 cm3 là:
36 400 : ( 50 x 20 ) = 36,4 ( cm )
a) Thể tích bể:
50.20.40 = 40000 (cm³)
b) Thể tích nước còn lại trong bể:
40000 - 3600 = 36400 (cm³)
Chiều cao mực nước còn lại trong bể:
36400 : 50 : 20 = 36,4 (cm)