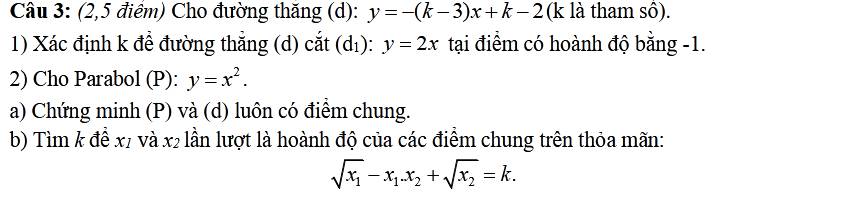
giúp em bài này với ạ , em cần gấp , em cảm ơn nhiều ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
\(P\geq \frac{(a^2+b^2+c^2)^2}{b+2c+c+2a+a+2b}=\frac{(a^2+b^2+c^2)^2}{3(a+b+c)}=\frac{(a^2+b^2+c^2)^2}{9}\)
Tiếp tục áp dụng BĐT Cauchy Schwarz:
$a^2+b^2+c^2\geq \frac{(a+b+c)^2}{1+1+1}=\frac{(a+b+c)^2}{3}=\frac{3^2}{3}=3$
$\Rightarrow P\geq \frac{3^2}{9}=1$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c=1$
Bạn lưu ý lần sau gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.

1: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó; ΔAEB vuông tại E
Xét tứ giác BHFE có \(\widehat{BHF}+\widehat{BEF}=90^0+90^0=180^0\)
nên BHFE là tứ giác nội tiếp
2: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔCAB vuông tại C có CH là đường cao
nên \(CH^2=AH\cdot HB\)
=>\(4\cdot CH^2=4\cdot AH\cdot HB\)
=>\(4\cdot AH\cdot HB=\left(2CH\right)^2=CD^2\)

Ms lớp 8 nhg lm thử hoii
Gọi số sản phẩm lm trong 1 ngày dự định là x(sản phẩm)
Số sản phẩm thực tế lm trong 1 ngày : x+10(sản phẩm)
Tổng sản phẩm thực tế: 600+50=650(sản phẩm)
Ta có pt:
\(\dfrac{600}{x}-\dfrac{650}{x+10}=2\)
\(\dfrac{600\left(x+10\right)}{x\left(x+10\right)}-\dfrac{650x}{x\left(x+10\right)}\)\(=\dfrac{2x\left(x+10\right)}{x+10}\)
\(600x+6000-650x=2x^2+20x\)
\(-50x+6000=2x^2+20x\)
\(x^2+35x=3000\)
\(x=40\)
=> Thời gian sx theo hợp đồng= \(\dfrac{600}{40}\)=15 ngày

Khoảng cách từ O đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\left(m^2+1\right)+0\cdot\left(-1\right)+2\right|}{\sqrt{\left(m^2+1\right)^2+1}}=\dfrac{2}{\sqrt{\left(m^2+1\right)^2+1}}\)
\(\sqrt{\left(m^2+1\right)^2+1}>=\sqrt{1+1}=\sqrt{2}\)
=>\(d\left(O;\left(d\right)\right)=\dfrac{2}{\sqrt{\left(m^2+1\right)^2+1}}< =\sqrt{2}\forall m\)
Dấu '=' xảy ra khi m=0

Gọi (d): y = kx + b
Do (d) đi qua M(0; 2) nên b = 2
⇒ (d): y = kx + 2
Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = kx + 2
⇔ x² = 2kx + 4
⇔ x² - 2kx - 4 = 0
∆' = (-k)² - 1.(-4)
= k² + 4 > 0 với mọi k ∈ R
Vậy (d) luôn cắt (P) tại hai điểm phân biệt A, B

Phương trình hoành độ giao điểm của (P) và (d):
-x² = -mx + m - 1
⇔ x² - mx + m - 1 = 0
∆ = (-m)² - 4.(m - 1)
= m² - 4m + 1
= m² - 4m + 4 - 3
= (m - 2)² - 3
Để (d) cắt (P) tại hai điểm phân biệt thì ∆ > 0
⇔ (m - 2)² - 3 > 0
⇔ (m - 2)² > 3
⇔ m - 2 < -√3 hoặc m - 2 > √3
*) m - 2 < -√3
⇔ m < 2 - √3
*) m - 2 > √3
⇔ m > 2 + √3
⇒ m < 2 - √3; m > 2 + √3 thì (d) cắt (P) tại hai điểm phân biệt
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = m
x₁x₂ = m - 1
1/x₁ + 1/x₂ = 3/2
⇔ (x₁ + x₂)/(x₁x₂) = 3/2
⇔ m/(m - 1) = 3/2
⇔ 2m = 3(m - 1)
⇔ 2m = 3m - 3
⇔ 3m - 2m = 3
⇔ m = 3 (loại)
Vậy không tìm được m thỏa mãn đề bài

Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=mx-2m+2\)
=>\(\dfrac{1}{2}x^2-mx+2m-2=0\)
\(\text{Δ}=\left(-m\right)^2-4\cdot\dfrac{1}{2}\left(2m-2\right)\)
\(=m^2-2\left(2m-2\right)=m^2-4m+4=\left(m-2\right)^2>=0\forall m\)
Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0
=>\(\left(m-2\right)^2>0\)
=>\(m-2\ne0\)
=>\(m\ne2\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m\\x_1x_2=\dfrac{c}{a}=\left(2m-2\right):\dfrac{1}{2}=4m-4\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x_2=8x_1\\x_1+x_2=2m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x_1=2m\\x_2=8x_1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_1=\dfrac{2}{9}m\\x_2=8\cdot\dfrac{2}{9}m=\dfrac{16}{9}m\end{matrix}\right.\)
\(x_1x_2=4m-4\)
=>\(\dfrac{2}{9}m\cdot\dfrac{16}{9}m=4m-4\)
=>\(\dfrac{32}{81}m^2-4m+4=0\)(1)
\(\text{Δ}=\left(-4\right)^2-4\cdot\dfrac{32}{81}\cdot4=\dfrac{784}{81}\)
Do đó: phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{4-\dfrac{28}{9}}{2\cdot\dfrac{32}{81}}=\dfrac{9}{8}\left(nhận\right)\\m_2=\dfrac{4+\dfrac{28}{9}}{2\cdot\dfrac{32}{81}}=9\left(nhận\right)\end{matrix}\right.\)
1:
Để (d) cắt (d1) thì \(-\left(k-3\right)\ne2\)
=>\(k-3\ne-2\)
=>\(k\ne1\)
Thay x=-1 vào (d1), ta được:
\(y=2\cdot\left(-1\right)=-2\)
Thay x=-1 và y=-2 vào (d), ta được:
\(-\left(k-3\right)\cdot\left(-1\right)+k-2=-2\)
=>\(k-3+k-2=-2\)
=>2k-5=-2
=>2k=3
=>k=1,5(nhận)
2:
a: Phương trình hoành độ giao điểm là:
\(x^2=-\left(k-3\right)x+k-2\)
=>\(x^2+\left(k-3\right)x-k+2=0\)
\(\text{Δ}=\left(k-3\right)^2-4\cdot1\left(-k+2\right)\)
\(=k^2-6k+9+4k-8=k^2-2k+1=\left(k-1\right)^2\)>=0 với mọi k
=>(P) luôn cắt (d)
b:
ĐKXĐ: k<=2
Theo vi-et, ta có:
\(x_1+x_2=-\dfrac{b}{a}=-k+3;x_1x_2=\dfrac{c}{a}=-k+2\)
\(\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=x_1+x_2+2\sqrt{x_1x_2}\)
\(=-k+3+2\sqrt{-k+2}\)
\(=\left(-k+2\right)+2\sqrt{-k+2}+1=\left(\sqrt{-k+2}+1\right)^2\)
=>\(\sqrt{x_1}+\sqrt{x_2}=\sqrt{-k+2}+1\)
\(\sqrt{x_1}+\sqrt{x_2}-x_1x_2=k\)
=>\(\sqrt{-k+2}+1-\left(-k+2\right)=k\)
=>\(\sqrt{-k+2}+1+k-2-k=0\)
=>\(\sqrt{-k+2}-1=0\)
=>-k+2=1
=>-k=-1
=>k=1(nhận)