\(\left(x^2+3^2\right).10+90=220\\ \Rightarrow\left(x^2+9\right).10=130\\ \Rightarrow x^2+9=13\\ \Rightarrow x^2=4\\ \Rightarrow x^2=2^2\\ \Rightarrow x=2.\)

Cần ghi rõ dấu.

       A = 1 + 2² + 2³ +...+ 2¹¹

     2A =       2² + 2³ +...+ 2¹¹ + 2¹²

2A - A =       2¹² - 1

       A =   2¹² - 1

Đặt \(A=1+2^2+2^3=..+2^{11}\\ \Rightarrow2A=2+2^3+2^4=..+2^{12}\\ \Rightarrow2A-A=2^{12}-1\\ \Rightarrow A=2^{12}-1\)

\(a,128-3.\left(x+4\right)=23\\ \Rightarrow3.\left(x+4\right)=105\\ \Rightarrow x+4=35\\ \Rightarrow x=31\\ b,\left[\left(4x+28\right).3+55\right]:5=35\\ \Rightarrow\left(4x+28\right).3+55=175\\ \Rightarrow4x+28.3=120\\ \Rightarrow4x+28=60\\ \Rightarrow4x=32\\ \Rightarrow x=8.\)

c) \(\left(12x-4^3\right).8^3=4.8^4\)

\(12x-64=4.8^4:8^3\)

\(12x-64=32\)

\(12x=32+64\)

\(12x=96\)

\(x=\dfrac{96}{12}\)

\(x=8\)

d) \(720:\left[41-\left(2x-5\right)\right]:5=35\)

\(720:\left(41-2x+5\right):5=35\)

\(720:\left(46-2x\right)=35.5\)

\(720:\left(46-2x\right)=175\)

\(46-2x=720:175\)

\(46-2x=\dfrac{144}{35}\)

\(2x=46-\dfrac{144}{35}\)

\(2x=\dfrac{1466}{35}\)

\(x=\dfrac{1466}{35}:2\)

\(x=\dfrac{733}{35}\)

Chiều rộng bằng: \(\dfrac{3}{16}\) chu vi

Chiều rộng bằng: \(\dfrac{3}{16}\) \(\times\) 2 = \(\dfrac{3}{8}\) (nửa chu vi)

Tỉ số chiều rộng so với chiều dài là: 3:(8-3) = \(\dfrac{3}{5}\)

Ta có sơ đồ:  

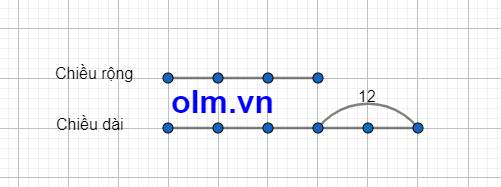
      Theo sơ đồ ta có:

Chiều rộng của hình chữ nhật là:

        12: (5- 3) \(\times\) 3 = 18(m)

Chiều dài của hình chữ nhật là:

        18 + 12 = 30 (m)

Diện tích hình chữ nhật là:

         30 \(\times\) 18 = 540 (m²)

Đáp số: 540 m² 

Đánh nhau ko

Các số chẵn đó là:

702; 704; 706; ...; 998; 1000

Số số hạng:

(1000 - 702) : 2 + 1 = 150 (số)

C = (1000 + 702) . 150 : 2 = 127650

Số số hạng:

(2017 - 101) : 4 + 1 = 480 (số)

B = (2017 + 101) . 480 : 2 = 508320

Đa tạ sư phụ Kiều Vũ Linh

a) Giả sử \(S_n=1^2+2^2+3^2+...+n^2=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}\left(\forall n\inℕ^∗\right)\)

- Với \(n=1:\)

\(S_n=\dfrac{1.\left(1+1\right)\left(2.1+1\right)}{6}=\dfrac{2.3}{6}=1\left(luôn.đúng\right)\)

- Với \(n=k:\) 

\(S_k=1^2+2^2+3^2+...+k^2=\dfrac{k\left(k+1\right)\left(2k+1\right)}{6}\left(\forall k\inℕ^∗\right)\left(luôn.đúng\right)\)

- Với \(n=k+1:\) 

\(S_{k+1}=1^2+2^2+3^2+...+k^2+\left(k+1\right)^2\)

\(\Rightarrow S_{k+1}=\dfrac{k\left(k+1\right)\left(2k+1\right)}{6}+\left(k+1\right)^2\)

\(\Rightarrow S_{k+1}=\dfrac{k\left(k+1\right)\left(2k+1\right)+6\left(k+1\right)^2}{6}\)

\(\Rightarrow S_{k+1}=\dfrac{\left(k+1\right)\left[k\left(2k+1\right)+6\left(k+1\right)\right]}{6}\)

\(\Rightarrow S_{k+1}=\dfrac{\left(k+1\right)\left[2k^2+7k+6\right]}{6}\)

\(\Rightarrow S_{k+1}=\dfrac{\left(k+1\right)\left[2k^2+3k+4k+6\right]}{6}\)

\(\Rightarrow S_{k+1}=\dfrac{\left(k+1\right)\left[2k\left(k+\dfrac{3}{2}\right)+4\left(k+\dfrac{3}{2}\right)\right]}{6}\)

\(\Rightarrow S_{k+1}=\dfrac{\left(k+1\right)\left[\left(2k+4\right)\left(k+\dfrac{3}{2}\right)\right]}{6}\)

\(\Rightarrow S_{k+1}=\dfrac{\left(k+1\right)\left[\left(k+2\right)\left(2k+3\right)\right]}{6}\) (Đúng với \(n=k+1\))

Vậy \(S_n=1^2+2^2+3^2+...+n^2=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}\left(\forall n\inℕ^∗\right)\left(dpcm\right)\)

Lớp 6 không chứng minh quy nạp!

\(S=1!+2!+3!+...+2023!\)

Ta thấy :

\(1!+2!+3!+4!=1+2+6+24=33\) không chia hết cho \(5\)

\(5!+6!+7!+8!+9!=\overline{.....5}⋮5\)

\(10!+11!+12!+...+2023!=\overline{.....0}⋮5\)

Vậy \(S=1!+2!+3!+...+2023!\) không chia hết cho \(5\)

Đa tạ suphu =))))

Bạn thi toán và tiếng: 9 <15

Bạn thi tiếng việt và tiếng anh: 10 < 15

Bạn thi toán và tiếng anh: 11 < 15

Vậy tại sao lại có 15 bạn thi 2 môn?

5³⁴ và 5³²

5³⁴ > 5³²