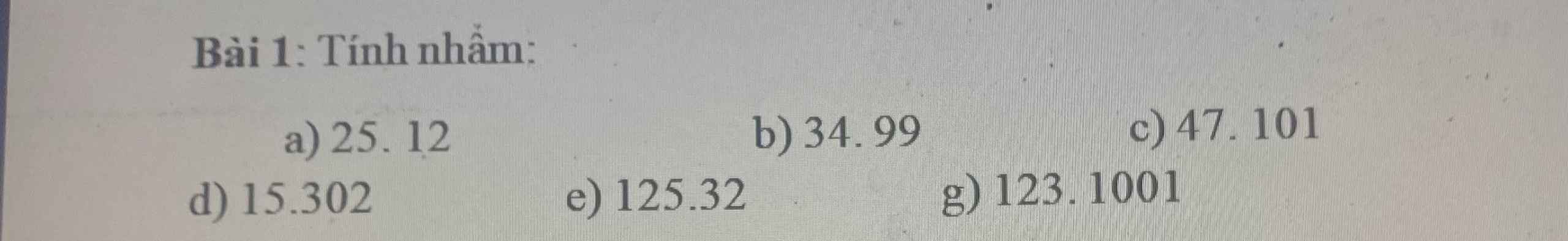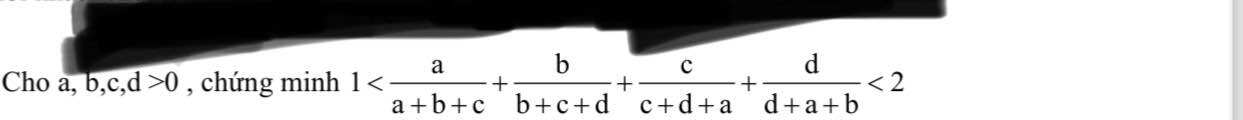
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(-5,1)^2 - (-5,1).4,9
= (-5,1).(-5,1) - (-5,1).4,9
= (-5,1). (-5,1 - 4,9)
= (-5,1). -10
= 51
6,5 .13 + 0,35.130
= 6,5 .13 + 0,35.10.13
= 6,5 .13 + 3,5.13
=(6,5 + 3,5).13
= 10.13
= 130

C là trung điểm của OA
=>\(OC=\dfrac{OA}{2}=4,5\left(cm\right)\)
Trên tia Ox, ta có: OC<OB
nên C nằm giữa O và B
=>OC+CB=OB
=>CB+4,5=12
=>CB=12-4,5=7,5(cm)

a) $25.12$
$=25.4.3$
$=100.3=300$
b) $34.99$
$=34.(100-1)$
$=34.100-34.1$
$=3400-34=3366$
c) $47.101$
$=47.(100+1)$
$=47.100+47.1$
$=4700+47=4747$
d) $15.302$
$=15.(300+2)$
$=15.300+15.2$
$=4500+30=4530$
e) $125.32$
$=125.8.4$
$=1000.4=4000$
g) $123.1001$
$=123.(1000+1)$
$=123.1000+123.1$
$=123000+123=123123$

Bạn tự vẽ hình nhé
Ta có E là trung điểm MN (gt)
\(\Rightarrow EM=EN=\dfrac{1}{2}MN\\ \Rightarrow EM=EN=6cm\)
Mà \(F\) là trung điểm \(EN\)
\(\RightarrowÈF=FN=\dfrac{1}{2}EN\\ \RightarrowÈ=FN=3cm\)
Vậy...
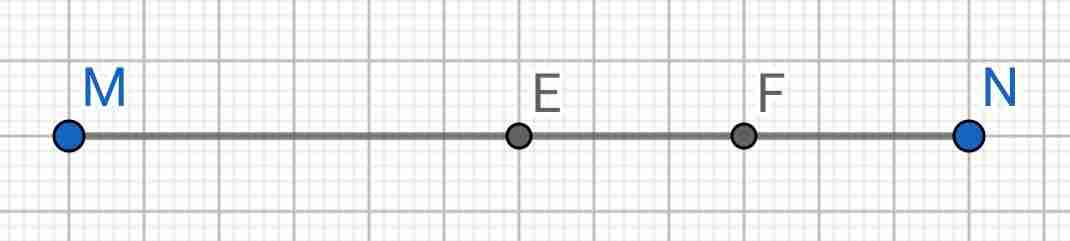
Do E là trung điểm của MN
=> NE = MN : 2
= 12 : 2
= 6 (cm)
Do F là trung điểm của NE
=> EF = NE : 2
= 6 : 2
= 3 (cm)

\(1+\dfrac{3}{2}+2+\dfrac{5}{2}+...+\dfrac{199}{2}+100\)
\(=\dfrac{2}{2}+\dfrac{3}{2}+\dfrac{4}{2}+...+\dfrac{200}{2}\)
\(=\dfrac{2+3+4+...+200}{2}\)
\(=\dfrac{199\cdot\dfrac{\left(200+2\right)}{2}}{2}=199\cdot\dfrac{202}{4}=10049,5\)
\(1+\dfrac{3}{2}+2+\dfrac{5}{2}+...+\dfrac{199}{2}+100\)
\(=\dfrac{2}{2}+\dfrac{3}{2}+\dfrac{4}{2}+\dfrac{5}{2}+...+\dfrac{199}{2}+\dfrac{200}{2}\)
\(=\dfrac{2+3+4+5+...+199+200}{2}\)
Số số hạng của \(2+3+4+5+..+199+200\) là :
\(\left(200-2\right):1+1=199\)
Tổng là :
\(\left(200+2\right)\times199:2=20099\)
Ta có :
\(\dfrac{20099}{2}\) \(=10049,5\)

Lời giải:
Ta thấy, với $a,b,c,d>0$ thì:
$\frac{a}{a+b+c}+\frac{b}{b+c+d}+\frac{c}{c+d+a}+\frac{d}{d+a+b}> \frac{a}{a+b+c+d}+\frac{b}{a+b+c+d}+\frac{c}{a+b+c+d}+\frac{d}{a+b+c+d}=\frac{a+b+c+d}{a+b+c+d}=1(*)$
Lại có:
Xét $\frac{a}{a+b+c}-\frac{a+d}{a+b+c+d}=\frac{-d(b+c)}{(a+b+c)(a+b+c+d)}<0$ với mọi $a,b,c,d>0$
$\Rightarrow \frac{a}{a+b+c}< \frac{a+d}{a+b+c+d}$
Tương tự: $\frac{b}{b+c+d}< \frac{b+a}{a+b+c+d}, \frac{c}{c+d+a}< \frac{c+b}{a+b+c+d}; \frac{d}{d+a+b}< \frac{d+c}{a+b+c+d}$
Cộng lại suy ra:
$\frac{a}{a+b+c}+\frac{b}{b+c+d}+\frac{c}{c+d+a}+\frac{d}{d+a+b}< \frac{a+d+b+a+c+b+d+c}{a+b+c+d}=\frac{2(a+b+c+d)}{a+b+c+d}=2(**)$
Từ $(*); (**)\Rightarrow$ đpcm.

11: \(2^2\cdot3^2-5\cdot2\cdot3=6^2-30=36-30=6\)
12: \(3^2\cdot5-2^2\cdot7+1\cdot5=9\cdot5-4\cdot7+5\)
=45-28+5
=50-28=22
13: \(5^2\cdot2-3^2\cdot4=25\cdot2-9\cdot4=50-36=14\)
14: \(7^2\cdot3-5^2\cdot3=49\cdot3-25\cdot3=24\cdot3=72\)
15: \(2^3\cdot3^2-4^2\cdot3=8\cdot9-16\cdot3=72-48=24\)
16: \(5^2\cdot2^3+3^2\cdot7-8^2\cdot2\)
\(=25\cdot8+9\cdot7-64\cdot2\)
=200+63-128
=263-128=135
17: \(\left(5\cdot2^2-20\right):5+3^2\cdot6=\left(5\cdot4-20\right):5+9\cdot6\)
=0+54
=54
18: \(\left(24\cdot5-5^2\cdot2\right):\left(5\cdot2\right)-3\)
\(=\left(120-50\right):10-3\)
=7-3=4
19: \(\left[\left(5^2\cdot2^3-7^2\cdot2\right):2\right]\cdot6-7\cdot2^5\)
\(=\left[5^2\cdot2^2-7^2\right]\cdot6-7\cdot32\)
=(100-49)*6-224
=51*6-224
=82
20: \(\left(6\cdot5^2-13\cdot7\right)\cdot2-2^3\left(7+3\right)\)
\(=\left(6\cdot25-91\right)\cdot2-8\cdot10\)
\(=\left(150-91\right)\cdot2-80\)
=118-80=38

\(a\left(b-c\right)-a\left(b+d\right)\\ =a\left[\left(b-c\right)-\left(b+d\right)\right]\\ =a\left(b-c-b+d\right)\\ =a\left(d-c\right)\)