Giải

Diện tích xung quanh của bể hình lăng trụ là:

        2,6 x 4 x 1,2  = 12,48 (m²)

Diện tích đáy bể là: 

       2,6 x 2,6 = 6,76 (m²)

Diện tích bể cần lát gạch là:

    12,48 + 6,76 = 19,24 (m²)

Diện tích một viên gạch là:

     40 x 30 = 1200 (cm²)

   1200cm² = 0,12m²

Vì 19,24 : 0,12 = 160,3

Vậy cần ít nhất số viên gạch để lát bể là:

    160 + 1  = 161 (viên)

Đáp số: ....

a.

Chiều rộng mảnh vườn là:

\(49:\dfrac{7}{5}=35\left(m\right)\)

Diện tích mảnh vườn là:

\(49\times35=1715\left(m^2\right)\)

b.

Diện tích trồng hoa là:

\(1715\times\dfrac{2}{5}=686\left(m^2\right)\)

Diện tích trồng rau là:

\(1715-686=1029\left(m^2\right)\)

c.

Số kg rau thu hoạch được là:

\(1029\times5:2=2572,5\left(kg\right)\)

              Giải:

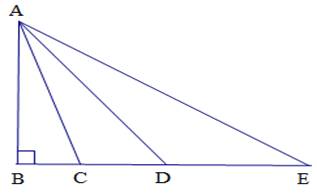
Ta có:    Xét tam giác vuông ABC vuông tại B nên cạnh AC là cạnh huyền, ta có: 

                 AC > AB ⁽¹⁾ (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)

            \(\widehat{ADB}\)  < 90⁰ (vì tam giác ADB vuông tại B)

           \(\widehat{ACD}\) = \(\widehat{ABC}\) + \(\widehat{BAC}\) (Góc ngoài tam giác bằng tổng hai góc trong không kề với nó)

        ⇒  \(\widehat{ACD}\)  = 90⁰ + \(\widehat{BAC}\) > \(\widehat{ADB}\)  = \(\widehat{ADC}\)

Xét tam giác ADC  có: 

            \(\widehat{ACD}\) > \(\widehat{ADC}\) (cmt)

            AD > AC ⁽²⁾(Trong tam giác góc đối diện với cạnh lớn hơn thì lớn hơn và ngược lại)

Chứng minh tương tự ta có:

         AE > AD ⁽³⁾

Từ (1) và (2) và (3) ta có:

       AE > AD > AC > AB 

Kết luận: AE > AD > AC > AB 

\(f'\left(x\right)=-4x^3.\left[f\left(x\right)\right]^2\Rightarrow\dfrac{f'\left(x\right)}{\left[f\left(x\right)\right]^2}=-4x^3\)

Lấy nguyên hàm 2 vế:

\(\Rightarrow-\dfrac{1}{f\left(x\right)}=\int-4x^3dx=-x^4+C\)

\(f\left(0\right)=1\Rightarrow-\dfrac{1}{f\left(0\right)}=0^4+C\Rightarrow C=-1\)

\(\Rightarrow-\dfrac{1}{f\left(x\right)}=-x^4-1\Rightarrow f\left(x\right)=\dfrac{1}{x^4+1}\)

\(\int\limits^3_0x^3.f\left(x\right)dx=\int\limits^3_0\dfrac{x^3}{x^4+1}dx\) (tích phân này rất đơn giản em tự tính hoặc bấm máy cũng được)

Hình vẽ đâu em nhỉ>

Trong 1 giờ vòi thứ nhất chảy được số phần bể là:

\(1:2=\dfrac{1}{2}\) (phần bể)

Trong 1 giờ vòi thứ hai chảy được số phần bể là:

\(\dfrac{1}{2}\times\dfrac{1}{3}=\dfrac{1}{6}\) phần bể

Trong 1 giờ cả 2 vòi cùng chảy được số phần bể là:

\(\dfrac{1}{2}+\dfrac{1}{6}=\dfrac{2}{3}\) (phần bể)

Cả hai vòi cùng chảy thì đầy bể sau số giờ là:

\(1:\dfrac{2}{3}=1,5\) (giờ)

Câu 5:

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔBAD=ΔBED

b: ΔBAD=ΔBED

=>DA=DE

mà DE<DC(ΔDEC vuông tại E)

nên DA<DC
ΔBAD=ΔBED

=>\(\widehat{BDA}=\widehat{BDE}\)

mà \(\widehat{BDA}=\widehat{DBK}\)(BK//AC)

nên \(\widehat{KBD}=\widehat{KDB}\)

=>ΔKBD cân tại K

1: Xét (O) có

ΔACB nội tiếp

AB là đường kính

Do đó: ΔACB vuông tại C

Xét (O) có

ΔADB nội tiếp

AB là đường kính

Do đó: ΔADB vuông tại D

Xét tứ giác BCKH có \(\widehat{BCK}+\widehat{BHK}=90^0+90^0=180^0\)

nên BCKH là tứ giác nội tiếp

b: Xét ΔAHK vuông tại H và ΔACB vuông tại C có

\(\widehat{HAK}\) chung

Do đó: ΔAHK~ΔACB

=>\(\dfrac{AH}{AC}=\dfrac{AK}{AB}\)

=>\(AK\cdot AC=AH\cdot AB\)

Xét ΔBHK vuông tại H và ΔBDA vuông tại D có

\(\widehat{HBK}\) chung

Do đó: ΔBHK~ΔBDA

=>\(\dfrac{BH}{BD}=\dfrac{BK}{BA}\)

=>\(BH\cdot BA=BK\cdot BD\)

\(AK\cdot AC+BK\cdot BD\)

\(=AH\cdot AB+BH\cdot AB=AB\left(BH+AH\right)=AB^2=4R^2\)

sai đề bài

Tổng số sách của 2 ngăn đầu tiên là:

64+75=139(quyển)

2 lần số quyển sách của ngăn thứ ba là:

139-3x17=88(quyển)

Số sách của ngăn thứ ba là:

88:2=44(quyển)