\(\dfrac{a}{2}=\dfrac{b}{3}\Rightarrow\dfrac{a}{10}=\dfrac{b}{15}\left(1\right)\)

\(\dfrac{b}{5}=\dfrac{c}{4}\Rightarrow\dfrac{b}{15}=\dfrac{c}{12}\left(2\right)\)

Từ (1) và (2) \(\Rightarrow\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{12}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{12}=\dfrac{a-b+c}{10-15+12}=\dfrac{21}{7}=3\)

\(\dfrac{a}{10}=3\Rightarrow a=3.10=30\)

\(\dfrac{b}{15}=3\Rightarrow b=3.15=45\)

\(\dfrac{c}{12}=3\Rightarrow c=3.12=36\)

Vậy \(a=30;b=45;c=36\)

a=30;b=45;c=36

\(3x^3+ax^2+bx+9⋮x^2-9\)

=>\(3x^3-27x+ax^2-9a+\left(b+27\right)x+9a+9⋮x^2-9\)

=>\(3x\left(x^2-9\right)+a\left(x^2-9\right)+9a+\left(b+27\right)x⋮x^2-9\)

=>\(\left\{{}\begin{matrix}9a=0\\b+27=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=0\\b=-27\end{matrix}\right.\)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

b: Xét ΔNAG và ΔNCP có

NA=NC

\(\widehat{ANG}=\widehat{CNP}\)(hai góc đối đỉnh)

NG=NP

Do đó: ΔNAG=ΔNCP

=>\(\widehat{NAG}=\widehat{NCP}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AG//CP

Ta có: AG//CP

AG\(\perp\)BC

Do đó: CP\(\perp\)BC

nhầm câu trả lời rồi hehe

Đặt ẩn phụ:

• Đặt 3/x = 5/y = 7/z = k
• Suy ra: x = 3/k, y = 5/k, z = 7/k

Thay vào phương trình:

• Thay y và z vào phương trình 3y - 2z = 99:
• • 3(5/k) - 2(7/k) = 99
  • 15/k - 14/k = 99
  • 1/k = 99
  • k = 1/99

Tìm giá trị của x, y, z:

• Thay k = 1/99 vào x, y, z:
• • x = 3 / (1/99) = 297
  • y = 5 / (1/99) = 495
  • z = 7 / (1/99) = 693

Vậy x = 297, y = 495, z = 693

Nhớ tick mik nhé

\(\dfrac{y}{5}=\dfrac{y\cdot3}{5\cdot3}=\dfrac{3y}{15}\\ \dfrac{z}{7}=\dfrac{z\cdot2}{7\cdot2}=\dfrac{2z}{14}\)

áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{3y}{15}=\dfrac{2z}{14}=\dfrac{3y-2z}{15-14}=\dfrac{99}{1}=99\\ \dfrac{3y}{15}=99=>y=495\\ \dfrac{2z}{14}=99=>z=693\\ x=\dfrac{3y}{5}=\dfrac{3\cdot495}{5}=297\)

vậy x = 297; y = 495; z = 693

Biểu thức đại số biểu thị nửa tổng bình phương của \(a\) và \(b\) là:

\(\frac{1}{2} \left(\right. a^{2} + b^{2} \left.\right)\)

Trong đó, \(a^{2}\) là bình phương của \(a\), và \(b^{2}\) là bình phương của \(b\).

\(3x^5+x^3-3x^5+1\\ =3x^3+1\)

đa thức bậc: 3;

hệ số cao nhất: 1;

hệ số tự do: 1

Saiii

Sửa đề : 97.103 thành 97.101
B = 1.5 + 5.9 + 9.13 + 13.17 + ... + 93.97 + 97.101
12B = 1.5.12 + 5.9.12 + 9.13.12 + 13.17.12 + ... + 93.97.12 + 97.101.12

12B = 1.5.12 + 5.9.(13 - 1) + 9.13.(17-5) + ... + 97.101.(105-93)
12B = 1.5.12 + 5.9.13 - 1.5.9 + 9.13.17 - 5.9.13 + ... + 97.101.105 - 93.97.101
12B = 1.5.12 - 1.5.9 + 97.101.105
12B = 5 . (12 - 9) + 1028685
12B = 5 . 3 + 1028685
12B = 12 + 1028685
12B = 1028700
B = 85725

Bài 4:

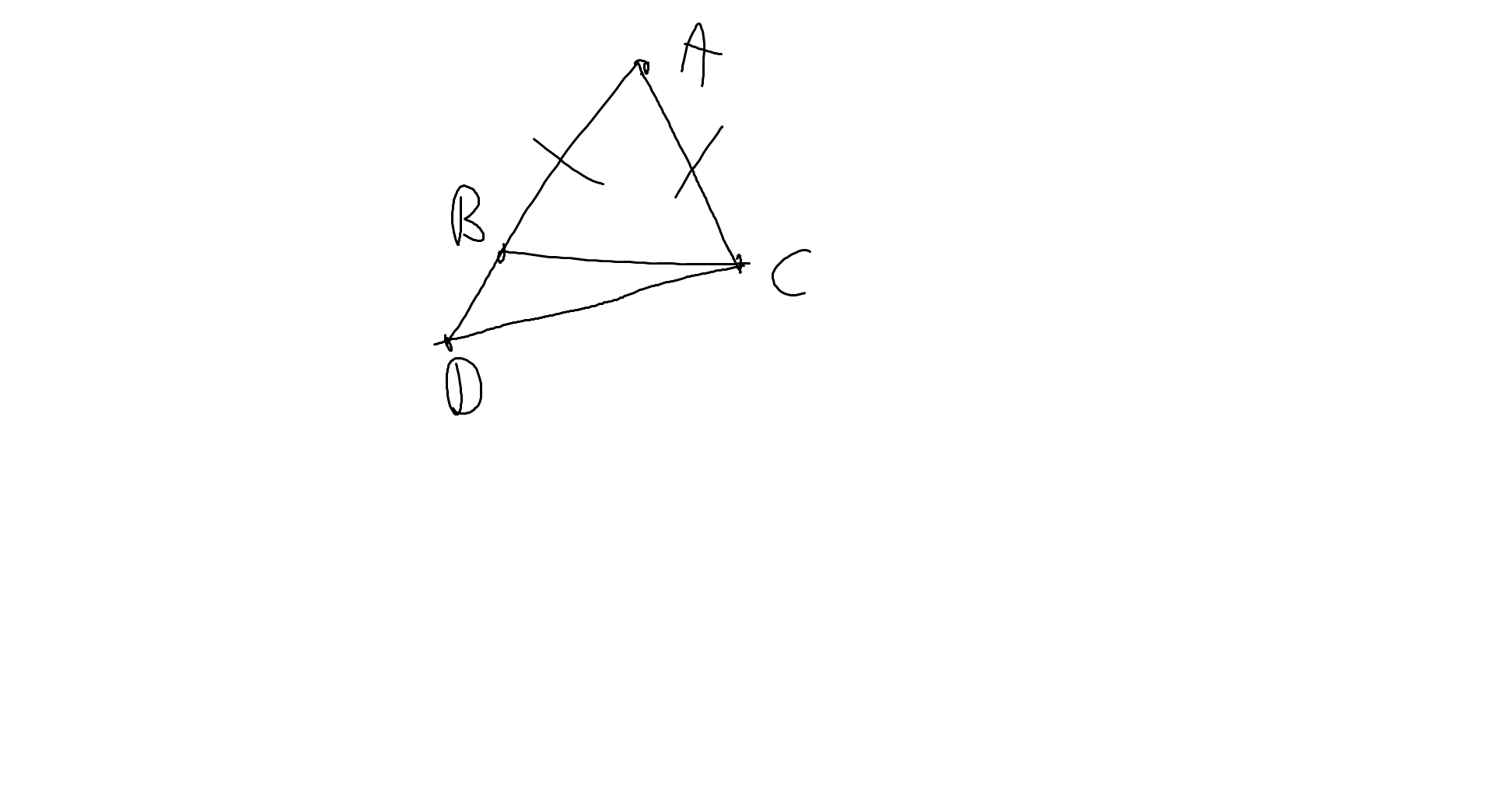
Xét ΔABC có \(\widehat{CBD}\) là góc ngoài tại đỉnh B

nên \(\widehat{CBD}=\widehat{BCA}+\widehat{BAC}\)

=>\(\widehat{CBD}>\widehat{ACB}\)

mà \(\widehat{ACB}=\widehat{ABC}\)(ΔABC cân tại A)

nên \(\widehat{CBD}>\widehat{CBA}\)

mà \(\widehat{CBD}+\widehat{CBA}=180^0\)

nên \(\widehat{CBD}>\dfrac{180^0}{2}=90^0\)

Xét ΔCBD có \(\widehat{CBD}>90^0\)

nên CD là cạnh lớn nhất trong ΔCBD

=>CD>CB

\(B=\left(\dfrac{1}{2^2}-1\right)\left(\dfrac{1}{3^2}-1\right)\cdot...\cdot\left(\dfrac{1}{2025^2}-1\right)\)

\(=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{2025}-1\right)\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{2025}+1\right)\)

\(=-\dfrac{1}{2}\cdot-\dfrac{2}{3}\cdot...\cdot\dfrac{-2024}{2025}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{2026}{2025}\)

\(=\dfrac{1}{2025}\cdot\dfrac{2026}{2}=\dfrac{1013}{2025}\)

=-\(\left(\frac12\cdot\frac32\right)\cdot\left(\frac23\cdot\frac43\right)\ldots\left(\frac{2024}{2025}\cdot\frac{2026}{2025}\right)\)

=-\(\left(\frac{1}{2025}\cdot\frac{2026}{2}\right)\)

=-\(\frac{1013}{2025}\)

\(\frac{a}{3}\) = \(\frac{b}{4}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{a}{3}\) = \(\frac{b}{4}\) = \(\frac{a+b}{3+4}\) = \(\frac{21}{7}\) = 3

a = 3.3 = 9

b = 3.4 = 12

Vậy (a; b) = (9; 12)