Bài học cùng chủ đề
- Dấu của tam thức bậc hai
- Tam thức bậc hai
- Định lí về dấu của tam thức bậc hai
- Cách xét dấu của tam thức bậc hai
- Giải bất phương trình bậc hai: sử dụng định lí về dấu của tam thức bậc hai
- Giải bất phương trình bậc hai: sử dụng đồ thị hàm số
- Tam thức bậc hai và định lí về dấu của tam thức bậc hai
- Xét dấu của tam thức bậc hai
- Giải bất phương trình bậc hai
- Bài toán sử dụng định lí về dấu có chứa tham số
- Phiếu bài tập: Dấu của tam thức bậc hai
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Cách xét dấu của tam thức bậc hai SVIP

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Cho tam thức bậc hai $f(x) = ax^2 + bx + c$, với $a \ne 0$.
+ Nếu $\Delta < 0$ thì $f(x)$ cùng dấu với hệ số $a$ với mọi số thực $x$;
+ Nếu $\Delta = 0$ thì $f(x)$ cùng dấu với hệ số $a$ với mọi $x \ne \dfrac{-b}{2a}$ và $f\left(-\dfrac b{2a}\right) = 0$;
+ Nếu $\Delta > 0$ thì tam thức $f(x)$ có hai nghiệm phân biệt $x_1$; $x_2$ ($x_1 < x_2$). Khi đó, $f(x)$ cùng dấu với hệ số $a$ với mọi $x \in (-\infty ; x_1) \cup (x_2 ; +\infty)$; và $f(x)$ trái dấu với hệ số $a$ với mọi $x \in (x_1 ; x_2)$.
Cho f(x)=x2+x+1 có Δ<0 và a=1>0 nên
Xét g(x)=−23x2+9x−227 có a=−23<0 và Δ=0.
g(x) có nghiệm kép x= nên g(x) 0 (cùng dấu với a) với mọi x .
(Kéo thả hoặc click vào để điền)
Tam thức bậc hai h(x)=2x2+6x−8 có nghiệm
Xét tam thức bậc hai f(x)=−x2−2x+8 có
Δ′= ; Hệ số a= .
Hàm số y=f(x)=ax2+bx+c có đồ thị hàm số như hình vẽ:
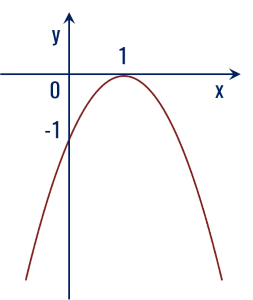
Tam thức f(x) có nghiệm kép x=1 ứng với trường hợp Δ
- =
- <
- >
Parabol có bề lõm hướng xuống nên hệ số a
- <
- >
Cho đồ thị của y=g(x) như hình vẽ:
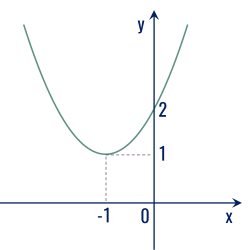
Đồ thị hàm số luôn nằm phía
- dưới
- trên
- có hai nghiệm phân biệt
- vô nghiệm
- có nghiệm duy nhất
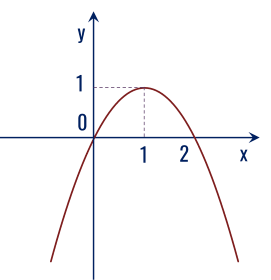
Dựa vào đồ thị hàm số y=g(x) trên, hoàn thành bảng xét dấu tam thức bậc hai g(x):
| x | −∞ 0 2 +∞ | ||
| g(x) |
|
||
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- chúng ta sẽ đi vận dụng nội dung lý
- thuyết này để xét dấu của các tam thức
- bậc hai với câu hỏi đầu tiên thấy yêu
- cầu xét dấu các tam thức bậc hai x bình
- cộng x cộng 1 trừ 3 phần 2x² + 9x - 27/2
- và 2x² + 6X - 8
- Ea Nếu thấy đặt FX = x² + x + 1 thì các
- bạn cho thể biết biết thức Delta hoặc là
- delta phẩy trong trường hợp này sẽ bằng
- bao nhiêu
- Nếu thể tính delta thì Delta sẽ bằng -3
- nhỏ hơn 0 và nhớ lại trong trường hợp
- Delta nhỏ hơn 0 FX sẽ luôn cùng dấu với
- hệ số a với mọi giá trị thực của x
- a ở đây là 1 lớn hơn 0 do đó FX cũng sẽ
- lớn hơn 0 với mọi x Vậy trong trường hợp
- Delta nhóm thông rất đơn giản chúng ta
- chỉ cần quan tâm hệ số a a mà âm thì FX
- của âm a mà Dương thì FX cũng Dương
- Còn trong trường hợp thứ hai thế đặt GX
- bằng -3x² + 9x - 27/2 các bạn tính delta
- sẽ cho kết quả là 0 Nếu Delta bằng 0 thì
- FX cùng dấu với a với mọi x khác trừ B
- trên 2A Còn trong trường hợp X = -b/2a
- thì FX sẽ bằng 0 vậy Ở đây Delta bằng 0
- thì GX sẽ có nghiệm kép x = 3 do đó
- trong trường hợp x = 3 GX sẽ bằng 0 Còn
- khi X mà khác 3 do a ở đây là bằng -3/2
- nhỏ hơn 0 nên GX cùng dấu với hệ số a
- cũng sẽ nhỏ hơn 0 với mọi x khác 3 đó là
- trường hợp Delta = 0 như vậy chỉ còn lại
- trường hợp Delta lớn không Liệu Ý C có
- vận dụng trường hợp này hay thành công
- thì thầy sẽ đặt hx bằng 2 bình cộng 6X -
- 8 và các bạn tính cho thầy nghiệm của
- tam thức bậc hai HD nhé
- nếu ta tính delta phẩy thì delta phẩy sẽ
- bằng 25 lớn hơn 0 nên hx trong trường
- hợp này sẽ có hai nghiệm phân biệt thầy
- gọi nhiệm Thứ nhất là X1 = -4 nghiệm thứ
- hai x2 = 1 và chúng ta sẽ tiến hành xét
- dấu của tam thức bậc hai trong trường
- hợp Delta lớn hơn 0 như sau các bạn đặc
- biệt chú ý nhé
- chúng ta sẽ sử dụng một đối tượng đó là
- bảng xét dấu bảng xét dấu của các bạn sẽ
- gồm có hai hàng hàng thứ nhất biểu diễn
- giá trị của x hàng thứ hai biểu diễn giá
- trị của FX trong bài này là hx thì
- thường bắt đầu từ âm vô cùng và kết thúc
- ở dương vô cùng trong các trường hợp mà
- tập xác định cụ thể thì chúng ta cũng sẽ
- thay đổi điểm đầu và điểm cuối phù hợp
- với tập xác định đó
- ở giữa âm vô cùng dương vô cùng chúng ta
- sẽ điền các nghiệm theo đường thứ tự nhé
- âm 4 nhỏ hơn chúng ta sẽ viết bên trái 1
- viết bên phải ở hàng X thì tương tự như
- một trục số vậy bằng âm 4 và x bằng 1
- thì hiển nhiên 2x = 0 rồi Vậy chúng ta
- sẽ điền các giá trị 0 thành cột ở đây
- Nếu như x nằm trong khoảng hai nghiệm
- thì sẽ trái dấu với hệ số a hệ số a ở
- đây Dương trong khoảng hai nghiệm tức là
- từ âm 4 đến 1 này hx sẽ nhận giá trị âm
- trái dấu mà trái dấu với Dương thì là âm
- ngược lại ngoài khoảng 2 nghiệm sẽ cùng
- dấu với a tức là nhận các giá trị dương
- và ta có đây chính là bảng xét dấu của
- tam thức bậc hai này
- và dựa vào bảng xét dấu chúng ta có thể
- kết luận được dấu của tam thức bậc hai
- như sau nếu x thuộc vào khoảng từ -4 đến
- 1 thì hx sẽ nhỏ hơn 0 ở đây là dấu trừ
- biểu thị cho 2x nhỏ hơn 0 này còn X mà
- nằm trong khoảng âm vô cùng đến -4 hợp
- với 1 đến dương vô cùng thì hx sẽ mang
- dấu dương tức là lớn hơn 0 với mọi x
- thuộc vào tập hợp này như vậy trong hỏi
- chấm 1 thầy đã lần lượt Xét dấu trong
- các trường hợp Delta nhỏ hơn 0 Delta
- bằng 0 và Delta lớn không tương tự như ý
- C này thì với câu hỏi hỏi chấm 2 các bạn
- sẽ lập cho thầy bảng xét dấu của tam
- thức fx bằng trừ x bình trừ 2X + 8 nhé
- tam thức bậc hai này có delta phẩy bằng
- trí lớn không Tức là FX sẽ có hai nghiệm
- phân biệt hai nghiệm phân biệt X1 bằng
- âm 4 và x2 = 2 Đây là bạn sẽ dấu thì
- chúng ta sẽ quan tâm tới hệ số a a đây
- bằng âm 1 nhỏ hơn 0 nên bạn sẽ dấu của
- FX sẽ như sau vẫn bắt đầu từ âm vô cùng
- đến dương vô cùng hai nghiệm ở đây là âm
- 4 và 2 chúng ta viết -4 nhỏ hơn ở bên
- trái 2 ở bên phải tại x = -4x = 2 giá
- trị FX sẽ bằng 0 Trong khoảng hai nghiệm
- thì trái dấu với a
- nên trong khoảng âm 4 đến 2 FX sẽ nhận
- giá trị dương ngoài khoảng 2 nghiệm sẽ
- nhận các giá trị âm và đây là bảng xét
- dấu của tam thức bậc hai trừ x bình trừ
- 2X + 8 nhé và để các bạn hiểu hơn mối
- quan hệ giữa Định lý về dấu của tam thức
- bậc hai với đồ thị hàm số bậc hai tương
- ứng thì chúng ta sẽ đến với câu hỏi hỏi
- chấm 3 thầy cho đồ thị của các hàm số GX
- như trong mỗi hình các bạn sẽ tìm nghiệm
- và lập bảng xét dấu các tam thức bậc hai
- GX ứng với các đồ thị hàm số trên nhé
- với đồ thị hàm số thứ nhất Chúng ta sẽ
- thấy được parabol tiếp xúc với trục Ox
- tại điểm x = 1 tam thức bậc hai GX của
- chúng ta sẽ có nghiệm duy nhất
- chính là trường hợp Delta bằng 0 GX cùng
- nghiệm kép đó nên thầy sẽ có bản Xét dấu
- của GX như sau có một là 1 thì chúng ta
- sẽ viết một ở đây x = 1 thì tương ứng
- với y = 0
- parabol có bề lõm quay xuống tức là A
- nhỏ hơn 0 Vậy thì GX sẽ nhận các giá trị
- âm trong các khoảng từ âm vô cùng đến 1
- và 1 đến dương vô cùng nhé
- ở trong hình số 2
- tức là tam thức bậc hai GX phủ nghiệm
- Vậy thì chúng ta sẽ chỉ cần quan tâm tới
- dấu của hệ số x bình phương Trong trường
- hợp này
- parabol có bề lõm quay lên thì a sẽ lớn
- hơn 0 do đó GX cùng dấu với a GX trong
- trường hợp này nhé
- đồ thị hàm số y bằng GX cắt trục Ox tại
- hai điểm điểm thứ nhất là có hoành độ x
- = 0 điểm thứ hai có hoành độ x = 2 Vậy
- thì chúng ta sẽ lập bảng xét dấu quan
- tâm tới hai giá trị không Và hai đó tại
- x = 0 x = 2 thì GX Chắc chắn là bằng 0
- rồi
- parabol có bị lõm hướng xuống thì a sẽ
- nhỏ hơn 0 Trong khoảng hai nghiệm GX sẽ
- trái dấu với a tức là GX sẽ mang dấu
- dương trong khoảng từ 0 đến 2
- ngoài đoạn 02 thì GX sẽ mang dấu âm đó
- là ta sử dụng định lý về dấu Còn nếu như
- quan sát vào vị trí của đồ thị hàm số
- với trục Ox ta sẽ thấy này ở đây đồ thị
- hàm số nếu x khác 1 nằm hoàn toàn phía
- dưới trục Ox nên các dấu của GX sẽ là
- dấu trừ hiển nhiên rồi
- ở hình thứ hai đô thị hàm số luôn nằm
- phía trên trục Ox thì tất nhiên GX phải
- mang dấu Dương Còn trong trường hợp số 3
- từ 0 đến 2 này khoảng từ 0 đến 2 đô thị
- hàm số luôn nằm phía trên trục Ox ứng
- với GX lớn hơn 0
- Còn khi X trong khoảng từ âm vô cùng đến
- 0 hoặc là 2 đến dương vô cùng thì GX sẽ
- mang dấu âm đù thì hàm số luôn nằm phía
- dưới trục Ox và Đó cũng chính là những
- nội dung kết thúc trong phần đầu tiên
- định lý về dấu của tam thức bậc hai
- trong phần này các bạn sẽ ghi nhớ cho
- thầy 3 trường hợp Delta nhỏ hơn 0 Delta
- bằng 0 Delta lớn hơn 0 giống của FX sẽ
- liên hệ với dấu của hệ số a tức là hệ số
- của x bình phương
Bạn có thể đăng câu hỏi về bài học này ở đây
