Bài học cùng chủ đề
- Mẫu số liệu ghép nhóm
- Tần số ghép nhóm - Bảng tần số ghép nhóm
- Tần số tương đối ghép nhóm. Bảng tần số tương đối ghép nhóm
- Biểu đồ tần số tương đối ghép nhóm
- Bảng tần số, tần số tương đối ghép nhóm
- Biểu đồ tần số, tần số tương đối ghép nhóm
- Vẽ biểu đồ và lập bảng tần số, tần số tương đối ghép nhóm
- Phiếu bài tập tuần
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Vẽ biểu đồ và lập bảng tần số, tần số tương đối ghép nhóm SVIP
Khối lượng (đơn vị: gam) của $30$ củ khoai tây thu hoạch được ở gia đình bác Ngọc là:
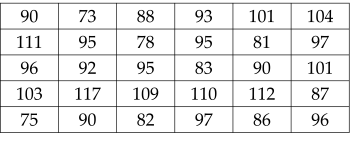
a) Hãy ghép các số liệu trên thành năm nhóm sau: $[70; 80)$, $[80; 90)$, $[90; 100)$, $[100; 110)$, $[110; 120)$. Tìm tần số của mỗi nhóm đó.
b) Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó.
Hướng dẫn giải:
a) Tần số của nhóm $[70; 80)$, $[80; 90)$, $[90; 100)$, $[100; 110)$, $[110; 120) $ lần lượt là:
$n_1 = 3; \,n_2 = 6; \,n_3 = 12;\, n_4 = 5;\, n_5 = 4$.
b) Bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó như sau:
| Nhóm | Tần số |
| $[70; 80)$ | $3$ |
| $[80; 90)$ | $6$ |
| $[90; 100)$ | $12$ |
| $[100; 110)$ | $5$ |
| $[110; 120) $ | $4$ |
| Cộng | $30$ |
Một cửa hàng sách thống kê số tiền (đơn vị: nghìn đồng) mà $60$ khách hàng mua sách ở cửa hàng đó trong một ngày. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm dưới đây:
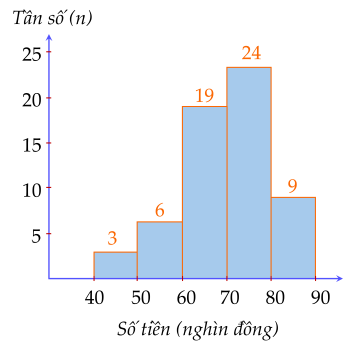
a) Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.
b) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.
Hướng dẫn giải:
a) Tần số tương đối của các nhóm lần lượt là:
$f_1=\dfrac{3}{60}⋅100\%=5\%$;
$f_2=\dfrac{6}{60}⋅100\%=10\%$;
$f_3=\dfrac{19}{60}⋅100\%\approx 31,67\%$;
$f_4=\dfrac{23}{60}⋅100\%\approx 38,33\%$;
$f_5=\dfrac{9}{60}⋅100\%=15\%$.
Ta có bảng tần số tương đối sau:
| Nhóm | $[40;50)$ | $[50;60)$ | $[60;70)$ | $[70;80)$ | $[80;90)$ |
| Tần số tương đối (%) | $5\%$ | $10\%$ | $31,67\%$ | $38,33\%$ | $15\%$ |
b) Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột:

Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng:

Thời gian chờ mua vé xem bóng đá của một số cổ động viên được cho như sau:
| Thời gian (phút) | $[0;5)$ | $[5;10)$ | $[10;15)$ | $[15;20)$ | $[20;25)$ | $[25;30)$ |
| Tần số (n) | $15$ | $38$ | $50$ | $27$ | $20$ | $10$ |
a) Lập bảng tần số tương đối ghép nhóm.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng cho bảng thống kê thu được ở câu a.
Hướng dẫn giải:
Tổng số cổ động viên là: $n = 15 + 38 + 50 + 27 + 20 + 10 = 160$.
a)
Tỉ lệ số cổ động viên có thời gian chờ từ $0$ phút đến dưới $5$ phút là:
$\dfrac{15}{160}⋅100\%=9,375\%$;
Tỉ lệ số cổ động viên có thời gian chờ từ $5$ phút đến dưới $10$ phút là:
$\dfrac{38}{160}⋅100\%=23,75\%$;
Tỉ lệ số cổ động viên có thời gian chờ từ $10$ phút đến dưới $15$ phút là:
$\dfrac{50}{160}⋅100\%=31,25\%$;
Tỉ lệ số cổ động viên có thời gian chờ từ $15$ phút đến dưới $20$ phút là:
$\dfrac{27}{160}⋅100\%=16,875\%$;
Tỉ lệ số cổ động viên có thời gian chờ từ $20$ phút đến dưới $25$ phút là:
$\dfrac{20}{160}⋅100\%=12,5\%$;
Tỉ lệ số cổ động viên có thời gian chờ từ $25$ phút đến dưới $30$ phút là:
$\dfrac{10}{160}⋅100\%=6,25\%$.
Ta có bảng tần số tương đối sau:
| Thời gian (phút) | $[0;5)$ | $[5;10)$ | $[10;15)$ | $[15;20)$ | $[20;25)$ | $[25;30)$ |
| Tần số tương đối % | $9,375$ | $23,75$ | $31,25$ | $16,875$ | $12,5$ | $6,25$ |
b) Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:
| Thời gian (phút) | $2,5$ | $7,5$ | $12,5$ | $17,5$ | $22,5$ | $27,5$ |
| Tần số tương đối % | $9,375$ | $23,75$ | $31,25$ | $16,875$ | $12,5$ | $6,25$ |
Ta có biểu đồ tần số tương đối dạng đoạn thẳng như sau:

Người ta trồng cà rốt và thử nghiệm một loại phân bón mới. Khi thu hoạch người ta đo chiều dài các củ cà rốt thu được kết quả sau:
| Chiều dài (cm) | $[15;16)$ | $[16;17)$ | $[17;18)$ | $[18;19)$ | $[19;20)$ | $[20;21)$ |
| Tần số (n) | $8$ | $17$ | $30$ | $28$ | $12$ | $5$ |
a) Lập bảng tần số tương đối ghép nhóm.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng thống kê thu được ở câu a.
Hướng dẫn giải:
Tổng số củ cà rốt là: $n = 8 + 17 + 30 + 28 + 12 + 5 = 100$.
Tỉ lệ số củ cà rốt có chiều dài từ $15$ cm đến dưới $16$ cm là:
$\dfrac{8}{100}⋅100\%=8\%$;
Tỉ lệ số củ cà rốt có chiều dài từ $16$ cm đến dưới $17$ cm là:
$\dfrac{17}{100}⋅100\%=17\%$;
Tỉ lệ số củ cà rốt có chiều dài từ $17$ cm đến dưới $18$ cm là:
$\dfrac{30}{100}⋅100\%=30\%$
Tỉ lệ số củ cà rốt có chiều dài từ $18$ cm đến dưới $19$ cm là:
$\dfrac{28}{100}⋅100\%=28\%$;
Tỉ lệ số củ cà rốt có chiều dài từ $19$ cm đến dưới $20$ cm là:
$\dfrac{12}{100}⋅100\%=12\%$
Tỉ lệ số củ cà rốt có chiều dài từ $20$ cm đến dưới $21$ cm là:
$\dfrac{5}{100}⋅100\%=5\%$
Ta có bảng tần số tương đối ghép nhóm sau:
| Chiều dài (cm) | $[15;16)$ | $[16;17)$ | $[17;18)$ | $[18;19)$ | $[19;20)$ | $[20;21)$ |
| Tần số tương đối (%) | $8$ | $17$ | $30$ | $28$ | $12$ | $5$ |
b) Biểu đồ tần số tương đối ghép nhóm dạng cột về số lượng cà rốt theo chiều dài:

