Tự luận (3 điểm) SVIP

Hướng dẫn giải:

Giả sử một lá bèo chiếm $x (0 < x < 1)$ mặt nước trong chậu. Sau 12 giờ, bèo sinh sôi phủ kín mặt nước trong chậu nên: ${{10}^{12}}.x=1\Rightarrow x=\dfrac{1}{{{10}^{12}}}$

Giả sử t giờ thì lá bèo phủ kín $\dfrac{1}{5}$ mặt nước trong chậu thì: $\dfrac{1}{10^{12}}.10^t=\dfrac{1}{5}$

$t-12=\log \dfrac{1}{5}$

$t\approx 11,3$(giờ)

Hướng dẫn giải:

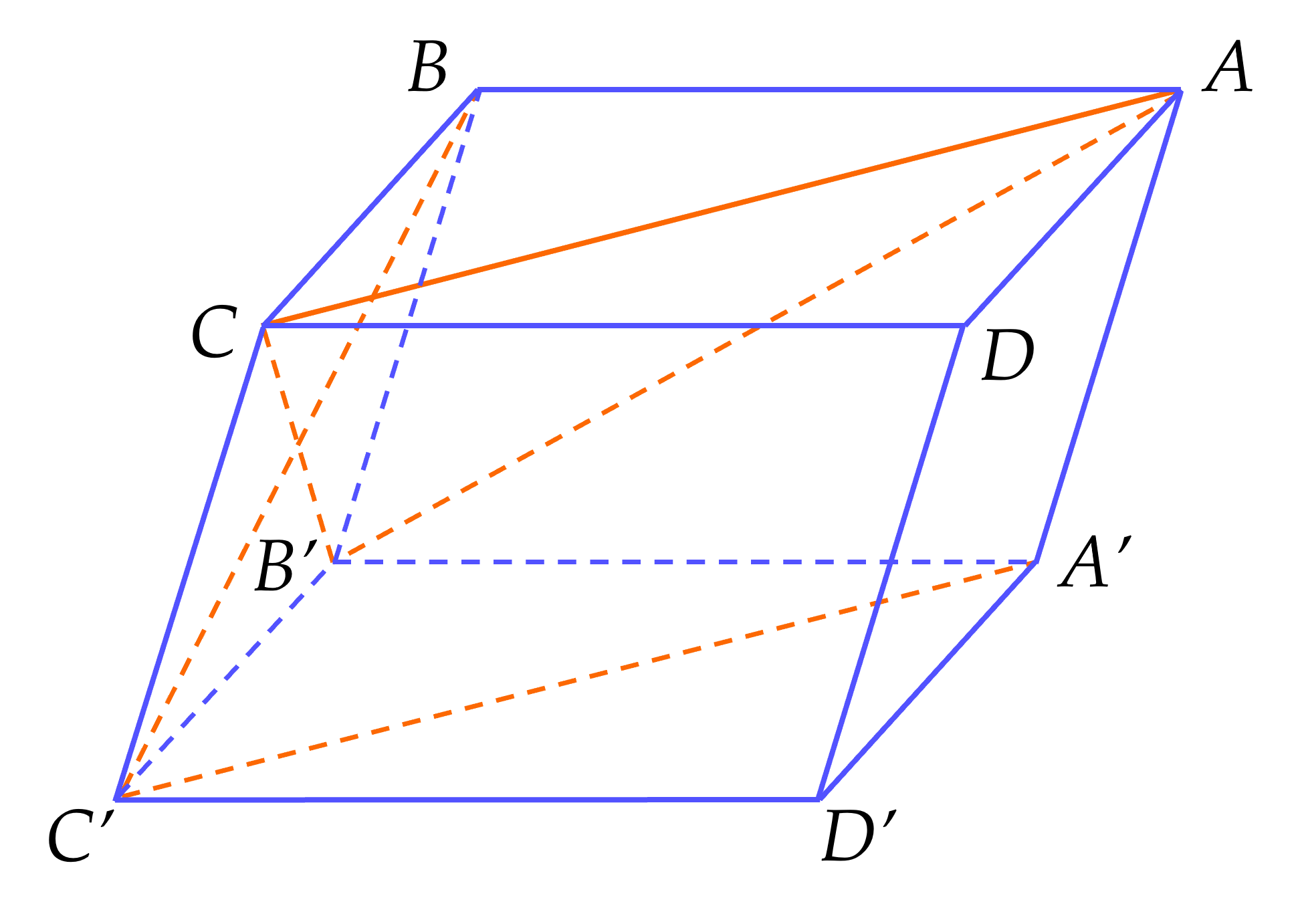
Ta có $d({C}';(AC{B}' ) )$$=d(B;(AC{B}' ) )$

Xét tứ diện $B.AC{B}'$ có

 +) $BA=BC=B{B}'=1$ nên điểm $B$ nằm trên trục của đường tròn ngoại tiếp $\Delta AC{B}'$.

Suy ra $BO\bot (AC{B}' )$ tại tâm $O$ của đường tròn ngoại tiếp $\Delta AC{B}'$.

+) $\widehat{CB{B}'}=60^\circ $, $\widehat{{B}'BA}=\widehat{ABC}=120^\circ $ nên áp dụng định lí cosin trong tam giác $\Delta {B}'BA$ và $\Delta ABC$ ta có $A{B}'=AC=\sqrt{3}$.

$d(B;(AC{B}' ))=BO=BA^2-R^2$ với $R$ là bán kính của đường tròn ngoại tiếp tam giác $\Delta AC{B}'$.

${{S}_{\Delta AC{B}'}}=\dfrac{A{B}'.C{B}'.AC}{4R}=\dfrac{AH.{B}'C}{2}$

$\Leftrightarrow \dfrac{\sqrt{3}\sqrt{3}}{4R}=\dfrac{\sqrt{3-\dfrac{1}{4}}}{2}$

$\Leftrightarrow R=\dfrac{3}{\sqrt{11}}$

$\Rightarrow BO=\sqrt{1-\dfrac{9}{11}}=\sqrt{\dfrac{2}{11}}=\dfrac{\sqrt{22}}{11}$

$\Rightarrow d({C}';(AC{B}' ) )=\dfrac{\sqrt{22}}{11}$.

Hướng dẫn giải:

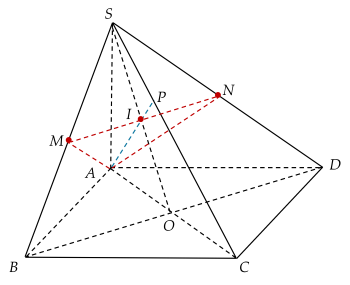
Gọi $AC\cap BD=O,\,SO\cap MN=I,\,AI\cap SC=P$.

$AN\bot (SCD )\Rightarrow AN\bot SC$ và $AM\bot (SBC )\Rightarrow AM\bot SC$.

Do đó: $SC\bot (AMN )$ hay $SC\bot (AMPN )$.

Suy ra: $(SB,(AMN ) )=(SM,(AMPN ) )=\widehat{SMP}$.

Ta có: $SM=\dfrac{S{{A}^{2}}}{SB}=\dfrac{2{{a}^{2}}}{\sqrt{2{{a}^{2}}+{{a}^{2}}}}=\dfrac{2a\sqrt{3}}{3}$;

$SP=\dfrac{S{{A}^{2}}}{SC}=\dfrac{2{{a}^{2}}}{\sqrt{2{{a}^{2}}+2{{a}^{2}}}}=a$.

Nên $\sin \widehat{SMP}=\dfrac{SP}{SM}=\dfrac{\sqrt{3}}{2}$

$\Rightarrow \widehat{SMP}=60^\circ$.