Tứ giác nội tiếp SVIP

Hướng dẫn giải:

a) Theo giả thiết, P là trung điểm dây AC nên đoạn thẳng IP vuông góc với dây AC. Hai tam giác AHI và API là hai tam giác vuông có chung cạnh huyền AI nên hai tam giác này cùng nội tiếp đường tròn đường kính AI. Do đó AHIP nội tiếp đường tròn đường kính AI.

Tâm K của đường tròn là trung điểm của AI.
b) Ta có AI = r, K là trung điểm AI nên \(KA=KI=\dfrac{r}{2}\).

Do đó, KI = IA \(-\) KA hay hai đường tròn (K) và (I) tiếp xúc nhau.

Hướng dẫn giải:

Theo giả thiết AB = AC nên \(\stackrel\frown{AB}=\stackrel\frown{AC}\)

Mà BF, CD là phân giác trong các góc B và C của tam giác ABC nên \(\stackrel\frown{FA}=\stackrel\frown{FA};\stackrel\frown{DA}=\stackrel\frown{DB}\).

Vì vậy nên \(\stackrel\frown{FA}=\stackrel\frown{FC}=\stackrel\frown{DA}=\stackrel\frown{DB}\left(=\dfrac{\stackrel\frown{AB}}{2}=\dfrac{\stackrel\frown{AC}}{2}\right)\)

\(\Rightarrow\) DA//BF và FA//CD.

Do đó ADEF là hình bình hành. Lại có AD = AF nên ADEF là hình thoi.

Hướng dẫn giải:

a) Có \(\widehat{APM}=\widehat{AHM}=\widehat{AQM}=90^o\) nên 5 điểm A, P, M, H, Q cùng thuộc đường tròn đường kính AM.
b) Vì AH là đường cao của tam giác đều ABC nên \(\widehat{BAH}=\widehat{HAC}=30^o\).

Vì A, P, M, H, Q cùng nằm trên đường tròn tâm O nên OP = OH = OQ = OM và \(\widehat{POH}=2\widehat{PAH}=60^o\) ; \(\widehat{QOH}=60^o\) suy ra OPH và OQH là hai tam giác đều, do đó OQHP là hình thoi.

c) Gọi r là bán kính đường tròn ngoại tiếp đa giác APMHQ thì AM = 2r và OPH, OQH là hai tam giác đều cạnh r. Do đó \(PQ=2.\dfrac{r\sqrt{3}}{2}=AM.\dfrac{\sqrt{3}}{2}\ge AH.\dfrac{\sqrt{3}}{2}\)

Do đó PQ ngắn nhất khi và chỉ khi M là trung điểm BC.

Hướng dẫn giải:

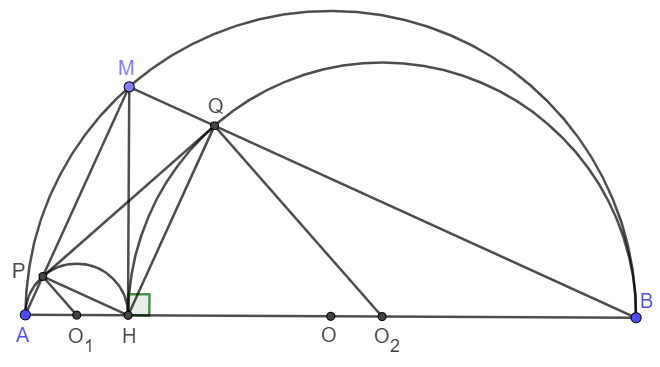
a) Vì AH, HB, AB đều là các đường kính của các nửa đường tròn (O₁) , (O₂) và (O) nên tứ giác MPHQ có ba góc P, Q, M vuông. Vì vậy nó là hình chữ nhật.

Từ đó, ta có HM = PQ.
b) Vì MHPQ là hình chữ nhật nên \(\widehat{MPQ}=\widehat{MHQ}=\widehat{MBH}\left(=\dfrac{\stackrel\frown{HQ}}{2}\right)\), do đó APQB là tứ giác nội tiếp.

c) Ta có \(\widehat{O_1PA}=\widehat{PAO_1}=90^o-\widehat{HMP}=90^o-\widehat{MPQ}\)

\(\Rightarrow\widehat{O_1PA}+\widehat{MPQ}=90^o\Rightarrow\widehat{O_1PQ}=90^o\) nên PQ tiếp xúc nửa đường tròn (O₁) tại P. 

Tương tự , PQ tiếp xúc (O₂) tại Q hay PQ là tiếp tuyến chung của hai nửa đường tròn (O₁) và (O₂).