Tứ giác nội tiếp SVIP

1. Đường tròn ngoại tiếp một tứ giác

Định nghĩa

Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).

Đường tròn đi qua bốn đỉnh của tứ giác là đường tròn ngoại tiếp tứ giác đó.

Tính chất

Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng $180^\circ$.

Ví dụ 1. Tìm $a$ trong hình bên dưới:

Lời giải

Ta có: $a + 56^\circ = 180^\circ$ (tổng hai góc đối của tứ giác nội tiếp).

$a = 180^\circ - 56^\circ$

$a = 124^\circ$

Ví dụ 2. Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$. Hai đường thẳng $AB$ và $DC$ cắt nhau tại $X$. Biết rằng $\widehat{DAB} = 70^\circ$, $\widehat{ABC} = 130^\circ$. Tính số đo của các góc $BCD$ và $BXC$.

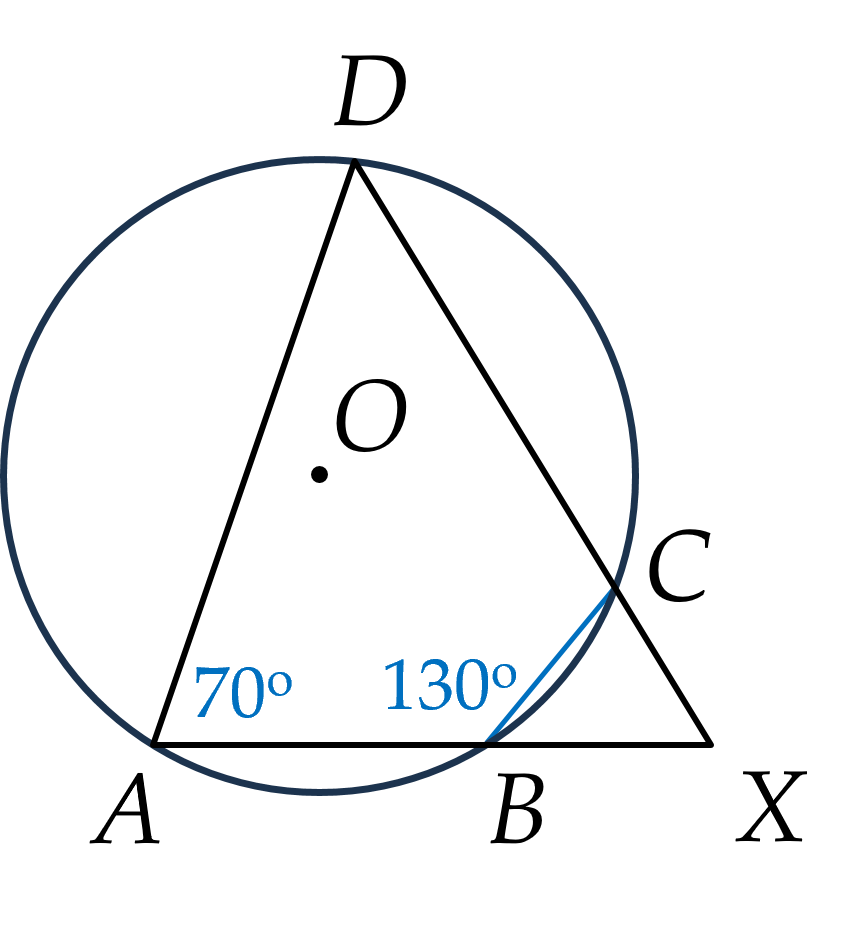
Lời giải

Vì $ABCD$ là tứ giác nội tiếp đường tròn $(O)$ nên các góc đối diện có tổng số đo bằng $180^\circ$.

Do đó: $\widehat{DAB} + \widehat{BCD} = 180^\circ$

$\widehat{BCD} = 180^\circ - \widehat{DAB} = 180^\circ - 70^\circ = 110^\circ$

$\widehat{ABC} + \widehat{CDA}= 180^\circ$

$\widehat{CDA} = 180^\circ - \widehat{ABC} = 180^\circ - 130^\circ = 50^\circ$

Vì tổng các góc trong tam giác $AXD$ bằng $180^\circ$ nên:

$\widehat{BXC} = \widehat{AXD} = 180^\circ - \widehat{DAB} - \widehat{CDA} = 180^\circ - 70^\circ - 50^\circ = 60^\circ$.

2. Đường tròn ngoại tiếp hình chữ nhật, hình vuông

Nhận xét

Hình chữ nhật và hình vuông là các tứ giác nội tiếp.

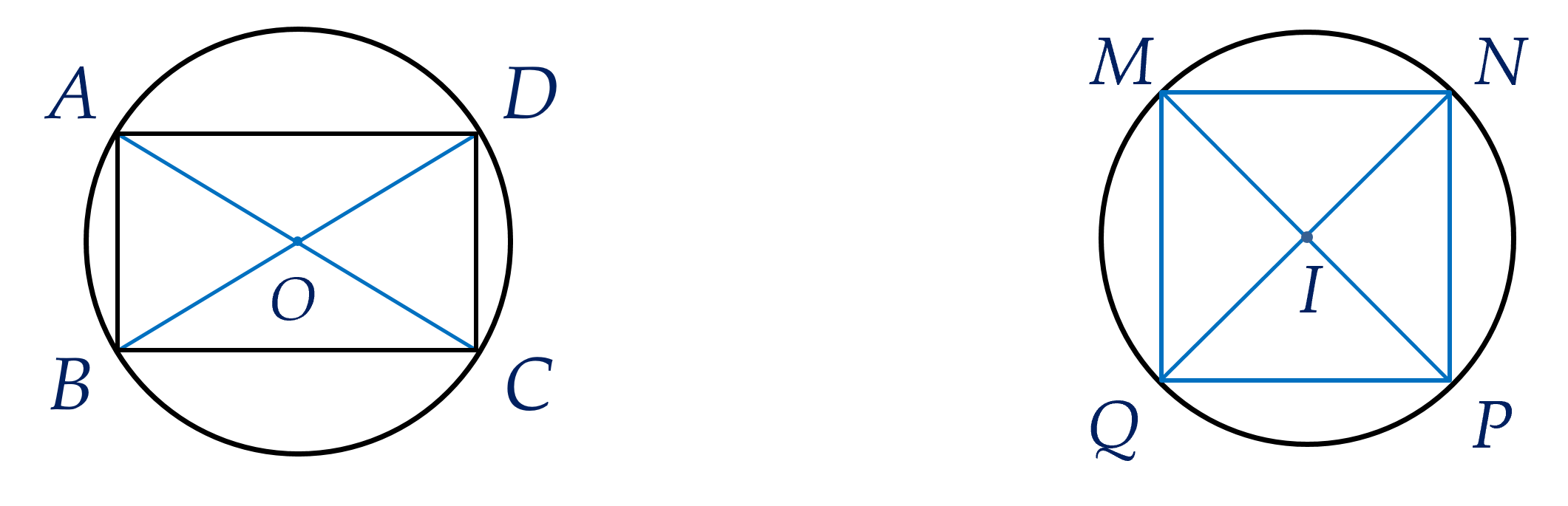
Đường tròn ngoại tiếp của chúng có tâm là giao điểm của hai đường chéo và bán kính bằng một nửa độ dài đường chéo.

Ví dụ 3. Xác định tâm; tính bán kính đường tròn ngoại tiếp hình chữ nhật trong hình vẽ sau:

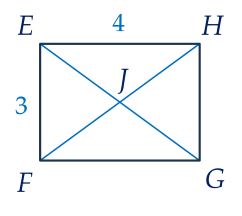
Lời giải

Hình chữ nhật $EFGH $ có $J$ là giao điểm của hai đường chéo.

Áp dụng định lí Pythagore vào tam giác $EFH$ vuông tại $E$, ta có:   

$FH^2 = EF^2 + EH^2 = 3^2 + 4^2 = 25$ hay $FH = 5$.

Suy ra đường tròn ngoại tiếp hình chữ nhật $EFGH$ có tâm $J$ và bán kính $R = FH \, : \, 2 = 2,5$.

Ví dụ 4. Xác định tâm; tính bán kính đường tròn ngoại tiếp hình vuông trong hình vẽ sau:

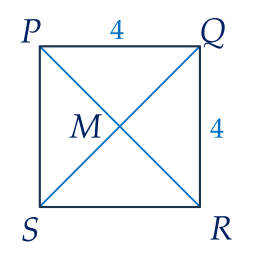
Lời giải

Hình vuông $PQRS$ có $M$ là giao điểm của hai đường chéo.

Áp dụng định lí Pythagore vào tam giác $PQR$ vuông tại $Q$, ta có: 

$PR^2 = PQ^2 + QR^2 = 4^2 + 4^2 = 32$ hay $PR = 4\sqrt2$.

Suy ra đường tròn ngoại tiếp hình vuông $PQRS$ có tâm $M$ và bán kính $R = PR \, :\,  2 = 2\sqrt2$.

Nhận xét

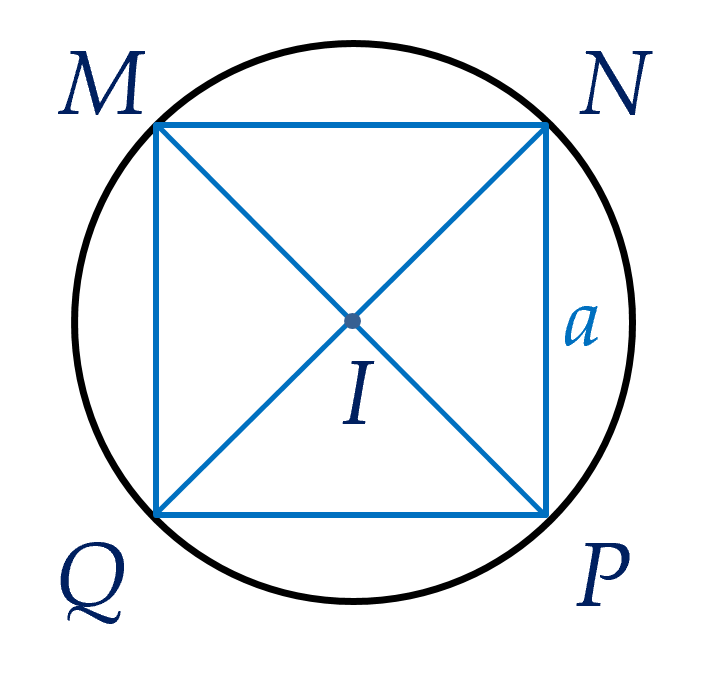
Bán kính của đường tròn ngoại tiếp hình vuông cạnh $a$ bằng $\dfrac{a\sqrt2}2$.

Ví dụ 5. Quan sát khung sắt, bạn Nam thấy hình vuông $ABCD$ nội tiếp đường tròn. Bạn Nam đo được cạnh của hình vuông đó bằng $2$ dm.

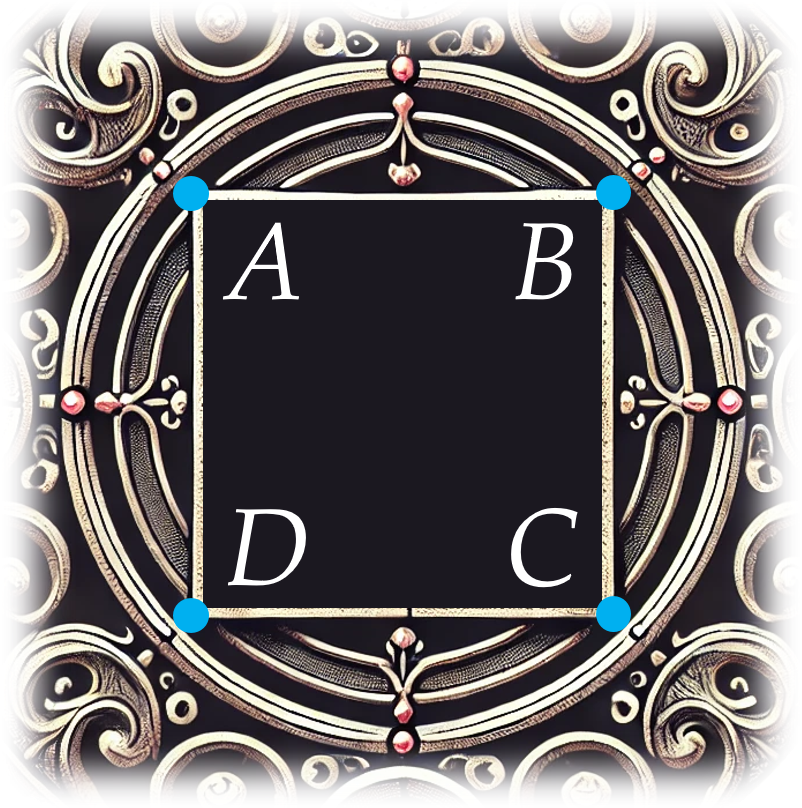
Chu vi của vòng sắt ứng với đường tròn ngoại tiếp hình vuông đó bằng bao nhiêu decimét? Làm tròn kết quả đến hàng phần mười.

Lời giải

Vì độ dài cạnh của hình vuông $ABCD$ là $2$ dm nên bán kính của đường tròn ngoại tiếp hình vuông đó là:

$2 \sqrt2 \,:\, 2 = 2$ (dm)

Vậy chu vi của vòng sắt ứng với đường tròn ngoại tiếp hình vuông đó là:

$2\sqrt2 \pi \approx 8,9$ (dm).