Chứng minh tứ giác nội tiếp SVIP

Hướng dẫn giải:

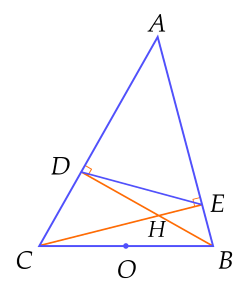
a) Chứng minh $BCDE$ là tứ giác nội tiếp.

Gọi $O$ là trung điểm $BC$.

Vì $BD, \, CE$ là các đường cao của $\Delta ABC$ nên $BD \bot AC$ và $CE \bot AB$

Suy ra $\widehat{BDC}=\widehat{BEC}=90^\circ$.

Xét tam giác $BDC$ có $\widehat{BDC}=90^\circ$ và $DO$ là đường trung tuyến ứng với cạnh huyền nên $OD=OC=OB=\dfrac{1}{2}BC$ (1)

Xét tam giác $BEC$ có $\widehat{BEC}=90^\circ$ và $EO$ là đường trung tuyến ứng với cạnh huyền nên $OE=OC=OB=\dfrac{1}{2}BC$ (2)

Từ (1) và (2) suy ra $OD=OE=OC=OB$.

Vậy tứ giác $BCDE$ nội tiếp được đường tròn có tâm $O$ là trung điểm $BC$.

b) Chứng minh $ADHE$ là tứ giác nội tiếp.

Vì $BD, \, CE$ là các đường cao của $\Delta ABC$ nên $BD \bot AC$ và $CE \bot AB$.

Gọi $M$ là trung điểm $AH$ (học sinh tự vẽ thêm trên hình)

Xét tam giác $ADH$ có $\widehat{ADH}=90^\circ$ và $DM$ là đường trung tuyến ứng với cạnh huyền nên $MD=MA=MH=\dfrac{1}{2}AH$ (3)

Xét tam giác $AEH$ có $\widehat{AEH}=90^\circ$ và $EM$ là đường trung tuyến ứng với cạnh huyền nên $ME=MA=MH=\dfrac{1}{2}AH$ (4)

Từ (3) và (4) suy ra $ADHE$ là tứ giác nội tiếp đường tròn tâm $M$ là trung điểm $AH$, đường kính $AH$.

Hướng dẫn giải:

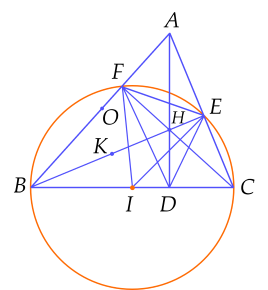
a) Chứng minh tứ giác $BFHD$ nội tiếp.

Xét đường tròn $(I)$ có $\widehat{CFB}=90^\circ$ (góc nội tiếp chắn nửa đường tròn)

Suy ra $CF \bot AB$.

$\widehat{CFB}=90^\circ$ (góc nội tiếp chắn nửa đường tròn)

Suy ra $BE \bot AC$

Mà $CF$ cắt $BE$ tại $H$ nên $H$ là trực tâm của tam giác $ABC$

Hay $AH \bot BC$, suy ra $\widehat{HDB}=90^\circ$

Gọi $K$ là trung điểm $BH$.

Xét tam giác $HDB$ có $\widehat{HDB}=90^\circ$ và $DK$ là đường trung tuyến ứng với cạnh huyền nên $KD=KH=KB=\dfrac{1}{2}BH$ (1)

Xét tam giác $HFB$ có $\widehat{HFB}=90^\circ$ và $EK$ là đường trung tuyến ứng với cạnh huyền nên $KE=KH=KB=\dfrac12HB$ (2)

Từ (1) và (2) suy ra $KB=KH=KF=KD$.

Vậy tứ giác $BFHD$ nội tiếp được đường tròn có tâm $K$ đường kính $BH$.

b) Chứng minh tứ giác $ABDE$ nội tiếp.

Gọi $O$ là trung điểm $AB$.

Xét tam giác $ADB$ có $\widehat{ADB}=90^\circ$ và $DO$ là đường trung tuyến ứng với cạnh huyền nên $OD=OA=OB=\dfrac{1}{2}AB$ (3)

Xét tam giác $AEB$ có $\widehat{AEB}=90^\circ$ và $EO$ là đường trung tuyến ứng với cạnh huyền nên $OE=OA=OB=\dfrac12AB$ (4)

Từ (3) và (4) suy ra $OD=OE=OA=OB$.

Vậy tứ giác $ABDE$ nội tiếp được đường tròn có tâm $O$ đường kính $AB$.

Hướng dẫn giải:

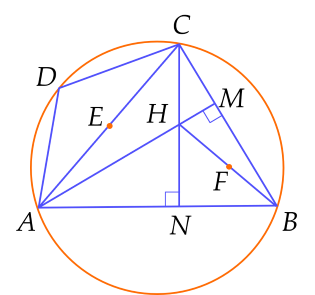
a) Chứng minh $\widehat{ABC}=\widehat{CHM}$.

Vì $AM, \, CN$ là các đường cao của $\Delta ABC$ nên $AM \bot BC$ và $CN \bot AB$

Suy ra $\widehat{BMH}=\widehat{BNH}=90^\circ$.

Gọi $F$ là trung điểm của $HB$.

Xét tam giác $HNB$ có $\widehat{HNB}=90^\circ$ và $NF$ là đường trung tuyến ứng với cạnh huyền nên $FN=FH=FB=\dfrac{1}{2}BH$ (1)

Xét tam giác $HMB$ có $\widehat{HMB}=90^\circ$ và $MF$ là đường trung tuyến ứng với cạnh huyền nên $FM=FH=FB=\dfrac{1}{2}BH$ (2)

Suy ra $BNHM$ là tứ giác nội tiếp đường tròn tâm $F$, đường kính $HB$.

Do đó $\widehat{MBN}+\widehat{NHM}=180^\circ$ (tổng hai góc đối bằng $180^\circ$.

hay $\widehat{CBA}+\widehat{NHM}=180^\circ$.

Mà $\widehat{MBN}+\widehat{NHM}=180^\circ$ (hai góc kề bù) do đó $\widehat{CBA}=\widehat{MBN}$.

b) Chứng minh $\widehat{ADC}=\widehat{AHC}$.

Tứ giác $BNHM$ nội tiếp nên $\widehat{MBN}+\widehat{NHM}=180^\circ$

Mà $\widehat{AHC}=\widehat{NHM}$ (đối đỉnh) nên $\widehat{MBN}+\widehat{AHC}=180^\circ$ hay $\widehat{ABC}+\widehat{AHC}=180^\circ$

Mặt khác tứ giác $BNHM$ nội tiếp đường tròn tâm $(O)$ nên $\widehat{ADC}+\widehat{ABC}=180^\circ$.

Do đó $\widehat{ADC}=\widehat{AHC}$.

c) Chứng minh $\widehat{MAC}=\widehat{MNC}$.

Ta chứng minh $ACMN$ là tứ giác nội tiếp.

Gọi $E$ là trung điểm $AC$.

Xét tam giác $AMC$ có $\widehat{AMC}=90^\circ$ và $ME$ là đường trung tuyến nên $EM=EC=EA=\dfrac{1}{2}AC$ (3) 

Xét tam giác $ANC$ có $\widehat{ANC}=90^\circ$ và $NE$ là đường trung tuyến nên $EN=EC=EA=\dfrac{1}{2}AC$ (4)

Từ (3) và (4) suy ra $EM=EN=EC=EA$.

Vậy tứ giác $ACMN$ nội tiếp được đường tròn có tâm $E$ đường kính $AC$.

Suy ra $\widehat{MAC}=\widehat{MNC}$ (hai góc nội tiếp cùng chắn cung $MC$ của đường tròn tâm $E$).

d) Chứng minh $\widehat{MAC}+90^\circ=\widehat{ANM}$.

Ta có $\widehat{MAC}+\widehat{ACM}=90^\circ$ (hai góc phụ nhau)

Hay $\widehat{ACM}=90^\circ-\widehat{MAC}$

Mà $\widehat{ACM}+\widehat{ANM}=180^\circ$ (tứ giác $ACMN$ nội tiếp được đường tròn) nên $90^\circ-\widehat{MAC}+\widehat{ANM}=180^\circ$

Suy ra $\widehat{MAC}+90^\circ=\widehat{ANM}$.

Hướng dẫn giải:

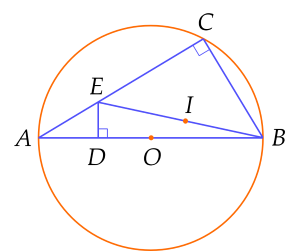
a) Tứ giác $BCED$ nội tiếp, $C$ thuộc đường tròn đường kính $AB$ suy ra \widehat{ACB}=90^\circ$ (góc nội tiếp chắn nửa đường tròn)

Suy ra $\widehat{ECB}=90^\circ$.

Mặt khác $ED \bot AB$ tại $D$ (gt) suy ra $\widehat{EDB}=90^\circ$.

Gọi $I$ là trung điểm của $BE$.

Xét tam giác $BCE$ có $\widehat{BCE}=90^\circ$ và $CI$ là đường trung tuyến ứng với cạnh huyền nên $IC=IE=IB=\dfrac{1}{2}BE$.

Xét tam giác $BED$ có $\widehat{BDE}=90^\circ$ và $DI$ là đường trung tuyến ứng với cạnh huyền nên $ID=IE=IB=\dfrac{1}{2}BE$.

Suy ra $BCED$ là tứ giác nội tiếp đường tròn tâm $I$, đường kính $BE$.

b) Xét $\Delta AED$ và $\Delta ABC$ có:

$\widehat{BAC}$ chung

$\widehat{ADE}=\widehat{ACB}=90^\circ$

Suy ra $\Delta AED \backsim \Delta ABC$ (g.g)

Suy ra $\dfrac{AE}{AB}=\dfrac{AD}{AC}$ (cặp cạnh tương ứng tỉ lệ) hay $AC.AE=AD.AB$.

Mà $D$ là trung điểm của $AO$ (gt) suy ra $AD=\dfrac{1}{2}AO$

$O$ là tâm đường tròn đường kính $AB$ (gt) nên $AO=\dfrac{1}{2}AB$

Suy ra $AD=\dfrac{1}{2}AO=\dfrac{1}{2}.\dfrac{1}{2}AB=\dfrac{1}{4}AB$

Do đó, $AC.AE=\dfrac{1}{4}AB.AB=\dfrac{AB^2}{4}$ (đpcm).

Hướng dẫn giải:

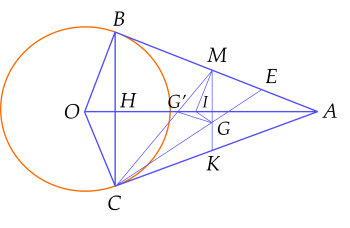
a) Do $AB, \, AC$ là hai tiếp tuyến cắt nhau của đường tròn $(O)$ nên $\widehat{ABO}=\widehat{ACO}=90^\circ$.

Gọi $I$ là trung điểm $OA$.

Xét tam giác $OAB$ vuông tại $B$ có $BI$ là trung tuyến ứng với cạnh huyền nên $IB = IA = IO = \dfrac12AO$ (1)

Xét tam giác $OAC$ vuông tại $C$ có $CI$ là trung tuyến ứng với cạnh huyền nên $IC = IA = IO = \dfrac12AO$ (2)

Từ (1) và (2) suy ra $IB = IC = IA = IO$.

Suy ra $B, \, C$ thuộc đường tròn tâm $I$ đường kính $OA$.

b) Ta có $AM.AO=\dfrac{AB}{2}.2AI=AB.AI$.

c) Gọi $E$ là trung điểm $MA$, do $G$ là trọng tâm $\Delta CMA$ nên $G \in CE$ và $\dfrac{GE}{CE}=\dfrac{1}{3}$.

Mặt khác $\dfrac{ME}{BE}=\dfrac{1}{3}$ $\Big($vì $ME=\dfrac{MA}{2}=\dfrac{MB}{2}$ nên $ME=\dfrac{BE}{3} \Big)$

Suy ra $\dfrac{GE}{CE}=\dfrac{ME}{BE}$, theo định lí Thalès đảo ta có:

$MG$ // $BC$.

d) Gọi $G'$ là giao điểm của $OA$ và $CM$ suy ra $G'$ là trọng tâm $\Delta ABC$.

Nên $\dfrac{G'M}{CM}=\dfrac{1}{3}=\dfrac{GE}{CE'}$

Theo định lý Thalès đảo ta có $GG'$ // $ME$ (1)

$MI$ là đường trung bình trong $\Delta OAB$ suy ra $ MI$ // $OB$, mà $AB \bot OB$ (cmt) nên $MI\bot AB$, nghĩa là $MI \bot ME$ (2).

Từ (1) và (2) suy ra $MI \bot GG'$,

Lại có $GI'\bot MK$ (vì $OA\bot MK$) nên $I$ là trực tâm $\Delta MGG'$

Suy ra $GI\bot G'M$ tức là $GI\bot CM$.