Phép cộng và phép trừ đa thức một biến SVIP

1. CỘNG HAI ĐA THỨC MỘT BIẾN

Ví dụ: Cho hai đa thức \(A=x^4-2x^3+3x^2-5x+1\) và \(B=x^4-2x^2+3x-2\). Tìm tổng \(A+B\).

Giải

\(A+B=\left(x^4-2x^3+3x^2-5x+1\right)+\left(x^4-2x^2+3x-2\right)\)

Cách 1. Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc

\(A+B=\left(x^4-2x^3+3x^2-5x+1\right)+\left(x^4-2x^2+3x-2\right)\)

\(=x^4-2x^3+3x^2-5x+1+x^4-2x^2+3x-2\)

\(=\left(x^4+x^4\right)-2x^3+\left(3x^2-2x^2\right)-\left(5x-3x\right)+\left(1-2\right)\)

\(=2x^4-2x^3+x^2-2x-1\).

Cách 2. Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột

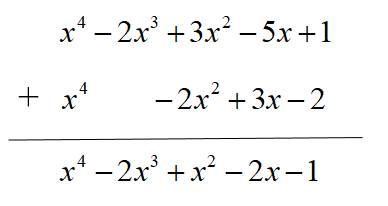
Vậy  \(A+B=x^4-2x^3+x^2-2x-1.\)

Chú ý. Phép cộng đa thức cũng có các tính chất như phép cộng các số thực:

Tính chất giao hoán: \(A+B=B+A.\)

Tính chất kết hợp: \(\left(A+B\right)+C=A+\left(B+C\right).\)

Cộng với đa thức không:\(A+0=0+A=A.\)

2. TRỪ HAI ĐA THỨC MỘT BIẾN

Ví dụ: Cho hai đa thức \(A=x^4-2x^3+3x^2-5x+1\) và \(B=x^4-2x^2+3x-2\). Tìm hiệu \(A-B\).

Giải

\(A-B=\left(x^4-2x^3+3x^2-5x+1\right)-\left(x^4-2x^2+3x-2\right)\)

Cách 1. Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc

\(A-B=\left(x^4-2x^3+3x^2-5x+1\right)-\left(x^4-2x^2+3x-2\right)\)

\(=x^4-2x^3+3x^2-5x+1-x^4+2x^2-3x+2\)

\(=\left(x^4-x^4\right)-2x^3+\left(3x^2+2x^2\right)-\left(5x+3x\right)+\left(1+2\right)\)

\(=-2x^3+5x^2-8x+3\).

Cách 2. Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột

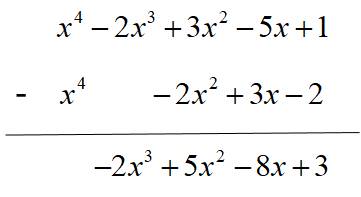
Vậy \(A-B=-2x^3+5x^2-8x+3.\)

Chú ý. Cho các đa thức \(P,Q,R\), ta có:

• Nếu \(Q+R=P\) thì \(R=P-Q.\)
• Nếu \(R=P-Q\) thì \(Q+R=P.\)