Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (8 điểm) SVIP
(3 điểm) Một đĩa tròn bằng bìa cứng được chia làm sáu phần bằng nhau và ghi các số 1, 2, 3, 4, 5, 6; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn và ghi lại số ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại. Mẫu số liệu dưới đây ghi lại số liệu sau 40 lần quay đĩa tròn:
1 1 3 5 4 6 1 2 6 4 1 5 5 2 4 3 3 6 5 2
5 6 2 3 3 4 2 3 3 4 4 5 4 6 1 2 3 5 6 6
a) Trong 40 số liệu thống kê ở trên, có bao nhiêu giá trị khác nhau?
b) Lập bảng tần số của mẫu số liệu thống kê đó. Vẽ biểu đồ tần số ở dạng biểu đồ cột của mẫu số liệu thống kê đó.
c) Lập bảng tần số tương đối của mẫu số liệu thống kê đó. Vẽ biểu đồ tần số tương đối ở dạng biểu đồ cột của mẫu số liệu thống kê đó.
Hướng dẫn giải:
a) Có 6 giá trị khác nhau.
b) Trong số 40 số liệu thống kê, có: 5 lần quay vào số 1, 6 lần quay vào số 2, 8 lần quay vào số 3, 7 lần quay vào số 4, 7 lần quay vào số 5 và 7 lần quay vào số 6.
Bảng tần số của mẫu số liệu thống kê:
| Giá trị | 1 | 2 | 3 | 4 | 5 | 6 |
| Tần số | 5 | 6 | 8 | 7 | 7 | 7 |
Biểu đồ dạng cột của tần số mẫu số liệu có dạng:
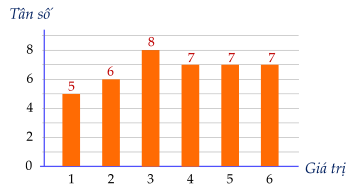
c) Các giá trị 1, 2, 3, 4, 5, 6 có tần số tương đối lần lượt là:
Bảng tần số tương đối:
| Giá trị | 1 | 2 | 3 | 4 | 5 | 6 |
| Tần số tương đối (%) | 12,5 | 15 | 20 | 17,5 | 17,5 | 17,5 |
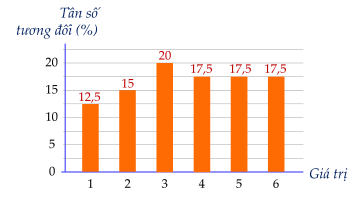
(2 điểm) Trên giá có 1 quyển sách Ngữ văn, 1 quyển sách Mĩ thuật và 1 quyển sách Công nghệ. Bạn Hà và bạn Thúy lần lượt lấy ra ngẫu nhiên quyển sách từ giá.
a) Xác định không gian mẫu của phép thử.
b) Xác định các kết quả thuận lợi cho mỗi biến cố sau: A: "Có 1 quyển sách Ngữ văn trong 2 quyển sách được lấy ra"; B: "Cả hai quyển sách lấy ra đều là sách Mĩ thuật".
Hướng dẫn giải:
a) = {(Ngữ văn; Mĩ thuật); (Ngữ văn; Công nghệ); (Mĩ thuật; Ngữ văn); (Mĩ thuật; Công nghệ); (Công nghệ; Mĩ thuật),;(Công nghệ; Ngữ văn)}.
b)
- Có 4 kết quả thuận lợi cho biến cố A là: (Ngữ văn; Mĩ thuật), (Ngữ văn; Công nghệ), (Mĩ thuật; Ngữ văn), (Công nghệ; Ngữ văn).
- Không có kết quả thuận lợi nào cho biến cố B.
(2,5 điểm) Cho đường tròn $(O; R)$ và một điểm $ A$ sao cho $OA = 2R$, vẽ các tiếp tuyến $AB$, $AC$ với đường tròn $(O; R)$, $B$ và $C$ là các tiếp điểm. Vẽ đường kính $BOD$. Gọi $I$ là giao điểm của đoạn thẳng $OA$ và đường tròn $(O; R)$.
a) Chứng minh bốn điểm $A$, $B$, $O$, $C$ cùng thuộc một đường tròn.
b) Đường trung trực của $BD$ cắt $AC$ và $CD$ lần lượt tại $S$ và $E$. Chứng minh rằng tứ giác $OCEA$ là hình thang cân.
c) $K$ là giao điểm của tia $SI$ và $AB$. Tính theo $R$ diện tích của tứ giác $AKOS$.
Hướng dẫn giải:
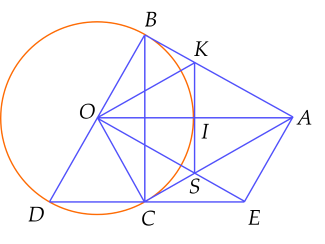
a) Ta có: $OA=2R$ mà $OI+IA=OA$ nên $R+IA=2R$.
Suy ra $OI=IA=R=\dfrac{OA}{2}$.
Theo đề bài $AB$ là tiếp tuyến của $(O; R)$ nên ta có $\widehat{OBA}=90^\circ$.
Xét $\Delta OBA$ vuông tại $B$ có: $BI$ là đường trung tuyến ứng với $OA$.
Suy ra $IB=IO=IA=\dfrac{OA}{2}$.
Do đó $O$, $B$, $A$ cùng thuộc đường tròn tâm $I$ đường kính $OA$ (1).
Chứng minh tương tự ta có $O$, $C$, $A$ cùng thuộc đường tròn đường kính $OA$ (2).
Từ (1) và (2) ta suy ra bốn điểm $A$, $B$, $O$, $C$ cùng thuộc một đường tròn. (điều phải chứng minh).
b) $AB$, $AC$ là tiếp tuyến của đường tròn $(O; R)$ nên $AB = AC$ (tính chất hai tiếp tuyến cắt nhau).
Suy ra $A$ nằm trên đường trung trực của $BC$.
Mà $OB = OC = R$.
Suy ra $O$ nằm trên đường trung trực của $BC$.
Do đó: $OA$ là đường trung trực của $BC$.
Nên $OA \perp BC$.
Xét $\Delta BCD$ có: $OB = OC = R$.
Mà $CO$ là trung tuyến ứng với $BD$ suy ra $\Delta BCD$ vuông tại $C$.
Suy ra $BC \perp DC$.
Do đó $DC$ // $OA$ (Vì cùng vuông góc với $BC$) hay $CE$ // $OA$.
Do đó $OCEA$ là hình thang (3).
Vì đường trung trực của $BD$ cắt $CD$ tại $E$ nên $DO \perp OE$ nên $\widehat{DOE}=90^\circ$.
Xét $\Delta ODE$ và $\Delta BOA$ ta có:
$OB=OD=R$
$\widehat{BOA}=\widehat{ODE}$ (hai góc đồng vị)
$\widehat{OBA}=\widehat{DOE}=90^\circ$
Suy ra $\Delta ODE=\Delta BOA$ (g.c.g).
Suy ra $OE = AB$ (hai cạnh tương ứng).
Mà $AB = AC$ (chứng minh trên) nên ta có: $OE = AC$ (4).
Từ (3) và (4) suy ra tứ giác $OCEA$ là hình thang cân (điều phải chứng minh).
c) Vì $AB, \, AC$ là tiếp tuyến của đường tròn $(O ; R)$ nên $AO$ là tia phân giác của $\widehat{BAC}$ (tính chất hai tiếp tuyến cắt nhau).
Suy ra $\widehat{BAO}=\widehat{SAO}$.
Ta chứng minh được $AB$ // $OS$ (cùng vuông góc với $BD$) nên $\widehat{BAO}=\widehat{SOA}$.
Suy ra $\widehat{SAO}=\widehat{SOA}$ hay $\Delta SOA$ cân tại $S$.
Lại có $ SI$ là đường trung tuyến ($OI=IA=\dfrac{OA}{2}=R$).
Suy ra $SI \perp OA$ hay $KS \perp OA$ (5).
Vì $OS$ là đường trung trực của $BD$ (giả thiết) nên $OS \perp BO$.
Mà $AB \perp BO$ (do $AB$ là tiếp tuyến tại $B$ của $(O)$).
Suy ra $AB$ // $OS$.
Do đó $\widehat{IAK}=\widehat{IOS}$ (hai góc so le trong).
Xét $\Delta OIS$ và $\Delta AIK$ có:
$IO = IA$ (chứng minh trên)
$\widehat{AIK}=\widehat{OIS}=90^\circ$ (do $KS \perp OA$)
$\widehat{IAK}=\widehat{IOS}$ (chứng minh trên)
Suy ra $\Delta OIS=\Delta AIK$ (g.c.g) nên $IK = IS$ (hai cạnh tương ứng).
Xét tứ giác $OKAS$ có: $I$ là trung điểm của $KS$ ($IK = IS$);
$I$ là trung điểm của $OA$ ($OI = IA$).
Suy ra tứ giác $OKAS$ là hình bình hành (dấu hiệu nhận biết) (6).
Từ (5) và (6) suy ra tứ giác $OKAS$ là hình thoi (dấu hiệu nhận biết).
Ta có $\Delta OAB$ vuông tại $B$ có $OA = 2OB = 2R$.
Suy ra $\widehat{OAB}=30^\circ$ hay $\widehat{KAI}=30^\circ$.
Xét $\Delta KAI$ vuông tại $I$ có: $\tan KAI=\tan 30^\circ=\dfrac{KI}{AI}$ (tỉ số lượng giác của góc nhọn)
Suy ra $KI=AI.\tan 30^\circ = \dfrac{\sqrt{3}}{3}R$
Suy ra $KS=2KI=\dfrac{2\sqrt{3}}{3}R$
Vậy diện tích của tứ giác $AKOS$ là:
${{S}_{AKOS}}=\dfrac{OA.SK}{2}=\dfrac{2R.\dfrac{2\sqrt{3}}{3}R}{2}=\dfrac{2\sqrt{3}}{3}R^2$.
(0,5 điểm) Hình vẽ mô tả mặt cắt của một chi tiết máy ép nhựa có dạng ở giữa là nửa hình vành khuyên giới hạn bởi hai nửa đường tròn ($O; 15$ cm), ($O; 10$ cm) và hai đầu là hai hình chữ nhật có chiều dài $15$ cm, chiều rộng $5$ cm.
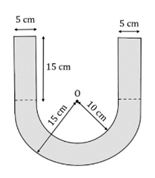
Tính diện tích mặt cắt của chi tiết máy ép nhựa đó (làm tròn kết quả đến hàng phần trăm của centimét vuông).
Hướng dẫn giải:
Diện tích mặt cắt của hai đầu hình chữ nhật là:
$2 . 5 . 15 = 150$ (cm2)
Diện tích hình tròn ($O; 15$ cm) là:
$S_1=\pi .15^2=225\pi $ (cm2)
Diện tích hình tròn ($O; 10$ cm) là:
$S_2=\pi .10^2=100\pi $ (cm2)
Nên diện tích nửa hình vành khuyên giới hạn bởi hai nửa đường tròn là:
$\dfrac{S_1-S_2}{2}=\dfrac{225\pi -100\pi }{2}=62,5\pi \approx 196,35$ (cm2)
Suy ra diện tích mặt cắt của chi tiết máy ép nhựa đó là:
$150 + 196,35 = 346,35$ (cm2)
Vậy diện tích mặt cắt của chi tiết máy ép nhựa đó là $346,35$ cm2.
